👨‍🏫 본 글은 칸 아카데미의 수업을 듣고 정리한 글 입니다.

• Orthogonal complements
• dim(v) + dim(orthogonal complement of v) = n
• Representing vectors in $r_n$ using subspace members
• Orthogonal Complement of the orthogonal Complement
• Orthogonal Complement of the null space
• Rowspace solution to $Ax=b$ example

---

Orthogonal complements

🎈 이번 시간에는 Orthogonal complements(직교여공간)에 대해 학습합니다.

🎈 $\mathbb{R}^n$의 부분공간 $V$의 Orthogonal complements(직교여공간)을 $V^{\perp}$ 라고 표현합니다. 이는 즉, 내적이 $\vec{0}$임을 의미합니다.

🎈 $V^{\perp}$을 부분공간이라고 부르기 위해선, 부분공간의 정의에 대해 만족해야하며, 이는 위의 식으로 만족함을 확인할 수 있습니다.

🎈 이전의 강의에서 임의의 행렬 $A$의 영공간이 $\vec{A^T}$의 행공간이라는 것을 학습했습니다. $N(A)$의 정의로 알 수 있듯이 $A$ $\cdot$ $\vec{x}$ = $\vec{0}$ 임을 만족해야합니다. 임의의 $\vec{V}_1$이 영공간 안에 포함되었다고 할 때, 이는 $A$의 각각의 열벡터($r_1 ... r_m$)과 orthogonal한 것을 알 수 있습니다. 이는 즉 어떠한 선형 결합과 비교해도 orthogonal하다는 것을 알 수 있습니다.

🎈 이에 대한 증명 과정으로, 열벡터($r_1 ... r_m$)들의 선형 결합인 $\vec{w}$는 행렬 $A$의 행공간 안에 포함되며, 이는 위의 $\vec{v}$와 내적이 0임을 알 수 있습니다. 이는 행렬 $A$의 영공간의 모든 요소들은 행렬 $A$의 행공간과 orthogonal 하는지 알 수 있습니다.

🎈 또 다른 $\vec{u}$가 행공간의 직교여공간에 포함되고, $\vec{w}$가 행공간에 포함된 벡터라고 이야기 할 때, 이 둘의 내적은 $\vec{0}$을 의미해야합니다. 여기서 $\vec{w}$를 각 $\vec{r}_j$(j= 1, ... ,m)를 표현하고, 이들과 각각의 $\vec{u}$의 내적이 0임을 알 수 있습니다. 이를 다시 표현하면 $A$ $\cdot$ $\vec{u}$ = 0 이라고 말할 수 있으며, 이는 $\vec{u}$이 $A$의 영공간에 포함되는 것을 알 수 있습니다.

🎈 결과적으로 영공간은 행공간의 직교여공간이라고 말할 수 있으며, Left 영공간은 열공간의 직교여공간이라는 것을 알 수 있습니다.

dim(v) + dim(orthogonal complement of v) = n

🎈 이번 강의에서는 V의 차원과 V의 직교여공간의 차원의 합이 n임을 학습합니다. 단, V는 $\mathbb{R}^n$의 부분공간입니다.

🎈 $\mathbb{R}^n$의 부분공간인 $V$의 차원 k와 $V$의 전치의 영공간의 차원의 합이 n임을 보여주고 있습니다.

Representing vectors in $r_n$ using subspace members

🎈 이번 강의에서는 이전의 강의에서 학습한 "dim(v) + dim(orthogonal complement of v) = n"의 성질에 대해 학습합니다.

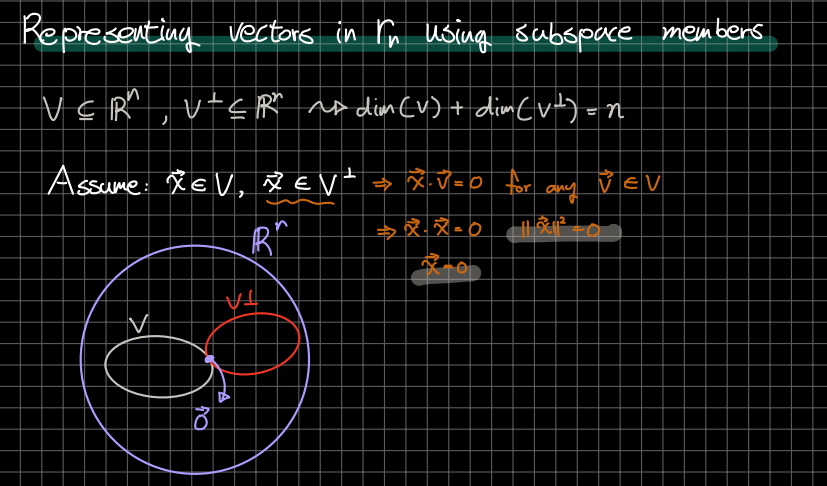
🎈 이전의 강의에서 $V$가 $\mathbb{R}^n$의 부분공간일 때, $V$의 차원과 $V^{\perp}$의 차원의 합이 $n$임을 학습했습니다. 먼저 $\vec{x}$가 $V^{\perp}$와 $V$에 포함된다고 가정할 때, 오직 $\vec{x}$ = $\vec{0}$만이 가능한 경우임을 알 수 있습니다.

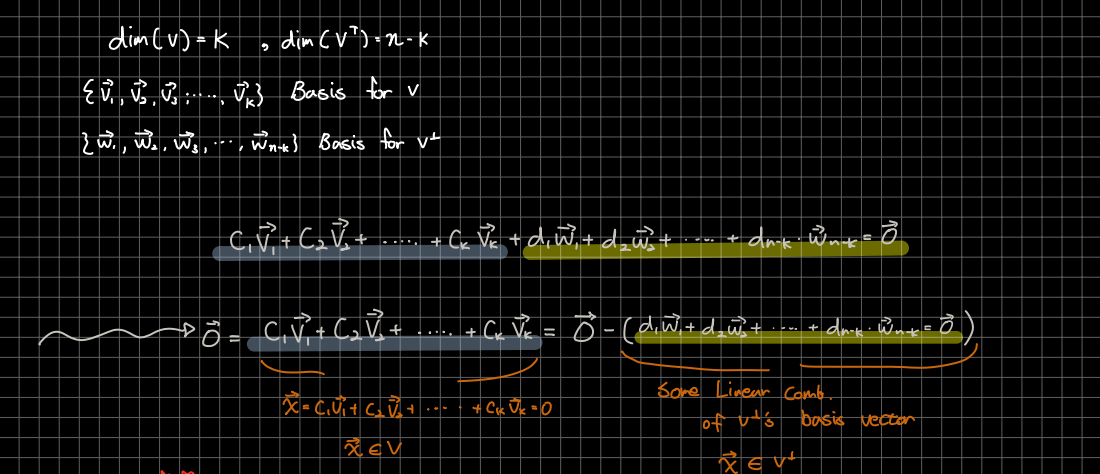
🎈 각각의 $V$의 차원과 $V^{\perp}$의 차원이 $V$와 $V^{\perp}$의 기저임을 알 수 있으며, 이는 즉 선형 독립함을 알 수 있습니다.

🎈 또한 두 차원의 합이 선형 독립한다는 것을 위의 과정으로 확인할 수 있으며, 이는 $\mathbb{R}^n$임을 알 수 있습니다.

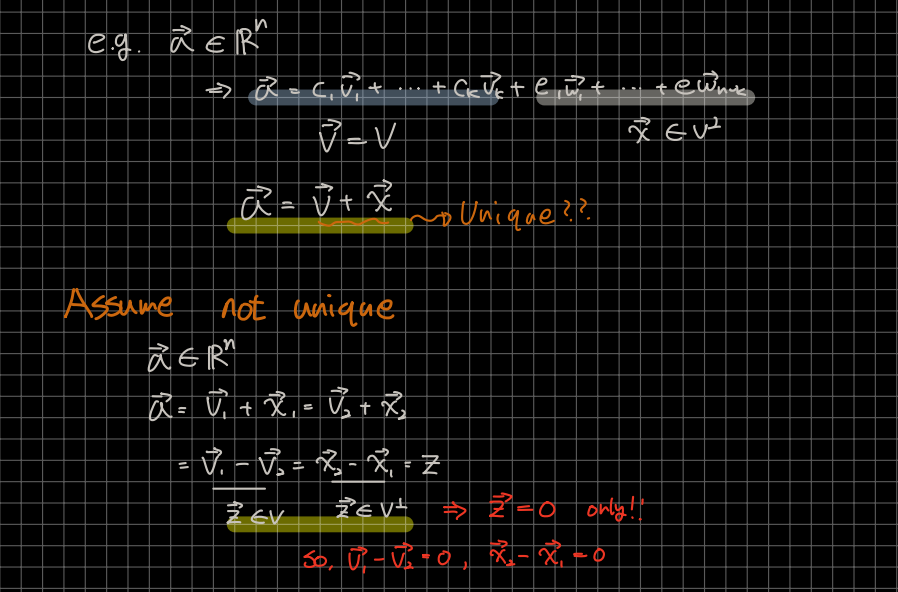
🎈 그렇다면 $\mathbb{R}^n$에 포함하는 임의의 $\vec{a}$를 $\vec{v}$ + $\vec{x}$라고 표현할 수 있습니다. $\vec{a}$ = $\vec{v}$ + $\vec{x}$이 unique한지 한번 확인해보겠습니다. 만약 unique하지 않다면, $\vec{a}$ = $\vec{v_1}$ + $\vec{x_1}$ = $\vec{v_2}$ + $\vec{x_2}$라고 표현할 수 있습니다. 이후의 위의 식의 과정을 확인해보면 처음에 학습했던 것과 동일하게 오직 $\vec{0}$일 때만 가정이 성립함을 알 수 있습니다.

Orthogonal Complement of the orthogonal Complement

🎈 이번 강의에서는 직교여공간의 직교여공간에 대해 학습합니다.

🎈 $(V^{\perp})^{\perp}$을 위의 그림과 같이 $V$ 공간 보다 살짝 더 큰 공간이라고 생각하면, 그 차이 공간에 대해 생각해보면, 위와 같이 증명할 수 있는데 결과적으로 $V^{\perp}$의 포함된 $\vec{w}$ = 0 이라는 것을 증명할 수 있습니다.

🎈 반대의 과정에서도 다음과 같이 증명할 수 있습니다. 결과적으로 $(V^{\perp})^{\perp} = V$ 라는 것을 알 수 있습니다.

Orthogonal Complement of the null space

🎈 이번 강의에선는 영공간의 직교여공간에 대해 학습합니다. 이는 이전의 강의에서 직교여공간의 직교여공간에 대해 학습했는데, 이를 적용하면 쉽게 알 수 있습니다.

Rowspace solution to $A\vec{x} = \vec{b}$ example

🎈 이번 시간에는 행공간과 $A\vec{x} = \vec{b}$의 해에 대해 학습합니다.

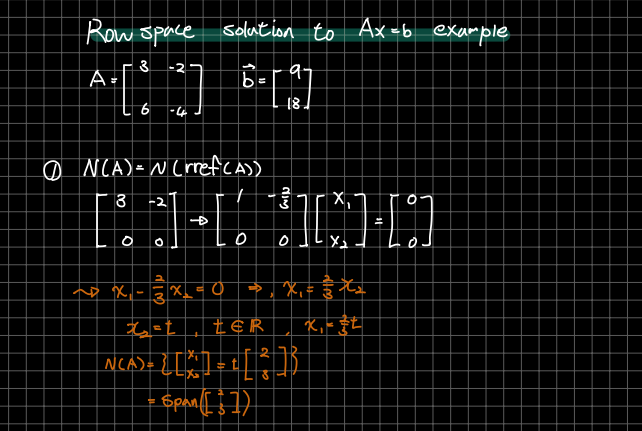
🎈 $A\vec{x} = \vec{b}$ 관계를 나타내기 위해 임의의 $A$와 $\vec{b}$를 다음과 같이 정의합니다. 먼저 $A$의 영공간을 찾아보면 기약행 사다리꼴 식을 사용해 span을 다음과 같이 찾을 수 있습니다.

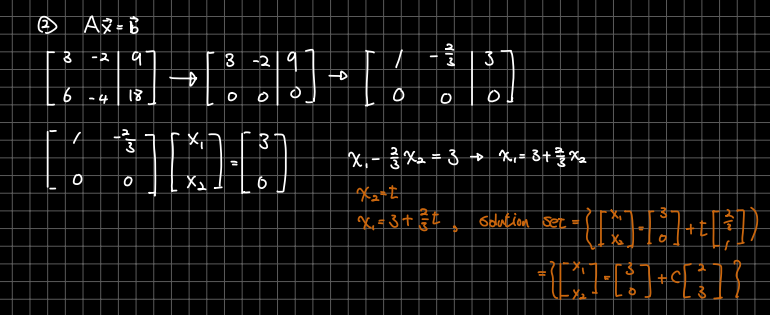
🎈 다음으로 $A\vec{x} = \vec{b}$의 해집합을 기약행 사다리꼴을 사용해 찾을 수 있습니다. 이는 영공간의 span에서 평행이동 한 것을 확인 할 수 있습니다.

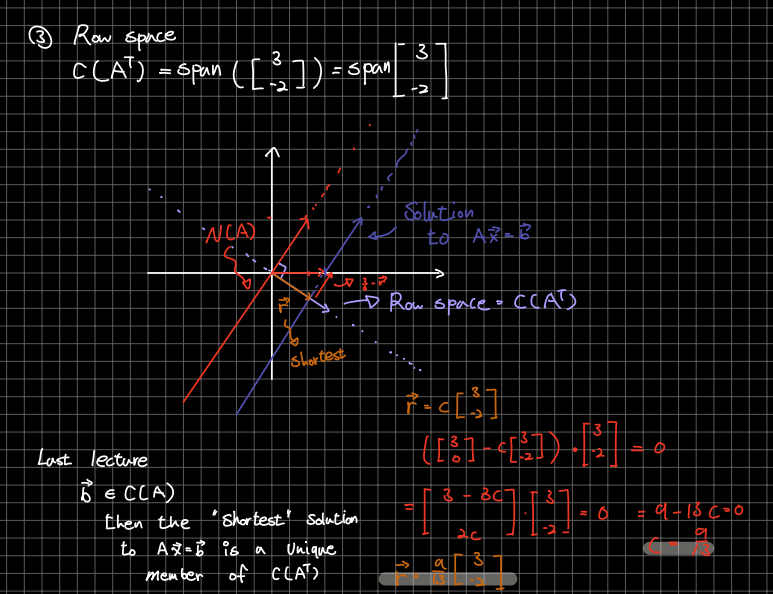
🎈 다음으로 $A$의 행공간에 대해 기약행사다리꼴을 구할 수 있습니다. 지금까지 구한 행공간과 해집합 그리고 영공간에 대한 span을 위와 같이 그래프 형태로 시각화 할 수 있습니다. $A\vec{x} = \vec{b}$에 해 중 가장 짧은 해는 행공간의 맴버임을 알 수 있습니다. 행공간의 행렬 $\vec{r}$가 가장 짧은 해 인것을 시각적으로 확인할 수 있습니다. 이를 통해 계산하면 $\vec{r}$의 정확한 값을 찾을 수 있습니다.