Query Optimization

사용자로부터 주어진 쿼리문을 평가하는 과정에서 equivalent한 관계대수식과, 각 연산에 대한 여러 알고리즘으로 인해 수많은 evaluation plan이 생길 수 있다. 이때 각 플랜의 비용은 큰 차이가 날 수 있기 때문에 쿼리문을 실행할 때에는 이 중 가장 효율적인 플랜을 선택해야하는데, 이 작업을 비용 기반 질의 최적화라고 한다.

비용 기반 질의 최적화는 다음과 같은 과정을 거쳐 이루어진다.

1. Equivalence rule을 통해 논리적으로 동등한 관계대수 식을 만들어낸다
2. 각 연산에 알고리즘을 배정하여 플랜을 만들어낸다
3. 각 플랜별 비용을 추정하여 가장 비용이 적은 플랜을 선택한다.

이때 각 플랜의 비용은 Base Table에 대한 통계치(튜플의 개수, 서로다른 값의 개수 등), 중간 결과에 대한 통계치, 각 연산의 비용식을 통해 계산한다. 이때 Base Table에 대한 통계치는 데이터베이스에 저장되어있고, 각 연산의 비용식은 이미 정해져있기 때문에 큰 문제가 없지만, 중간결과에 대한 통계치는 비용 추정 과정에서 직접 계산해야 하기 때문에 주의해야 한다.

Equivalance rule

Equivalance rule이란 두 식이 동등하다는 것을 보장하는 규칙으로 selection, projection, join, set operation에 대해 다음의 규칙이 성립한다.

• σθ1 ^ θ2(E) = σθ1(σθ2(E)) : Conjunctive selection
• σθ1(σθ2(E)) = σθ2(σθ1(E)) : selection 교환법칙
• πL1(πL2(...πLn(E))) = πL1(E) : 마지막 projection 빼고는 생략 가능
• σθ(E1 × E2) = E1 ⋈θ E2 : theta join 정의
• σθ1(E1 ⋈θ2 E2) = E1 ⋈θ1 ^ θ2 E2 : selection과 join 결합
• E1 ⋈ E2 = E2 ⋈ E1 : theta join 교환법칙
• (E1 ⋈ E2) ⋈ E3 = E1 ⋈ (E2 ⋈ E3) : theta join 결합법칙(Join ordering)
• (E1 ⋈θ1 E2) ⋈θ2 ^ θ3 E3 = E1 ⋈θ1 ^ θ3 (E2 ⋈θ2 E3) : theta join 결합법칙(θ2의 join attribute E2와 E3에만 있을 때)
• σθ1(E1 ⋈θ E2) = (σθ1(E1)) ⋈θ E2 : θ1의 join attribute가 E1에만 있으면 selection을 먼저 해도 된다.
• σθ1 ^ θ2(E1 ⋈θ E2) = (σθ1(E1)) ⋈θ (σθ2(E2)) : θ1과 θ2의 join attribute가 각각 E1, E2에만 있으면 selection을 먼저 해도 된다.
• πL1 ∪ L2(E1 ⋈θ E2) = πL1(E1) ⋈θ πL2(E2) : projection 분할 (θ의 join attribute가 L1 ∪ L2에만 있을 때)
• E1 ∪ E2 = E2 ∪ E1 / E1 ∩ E2 = E2 ∩ E1 : union, intersection 교환법칙
• (E1 ∪ E2) ∪ E3 = E1 ∪ (E2 ∪ E3) / (E1 ∩ E2) ∩ E3 = E1 ∩ (E2 ∩ E3) : union, intersection 결합법칙
• σ(E1 ∪ E2) = σ(E1) ∪ σ(E2) / σ(E1 ∩ E2) = σ(E1) ∩ σ(E2) / σ(E1 - E2) = σ(E1) - σ(E2) : union, intersection, difference 분배법칙(selection)
• σ(E1 ∩ E2) = σ(E1) ∩ E2 / σ(E1 - E2) = σ(E1) - E2 : intersection, difference 분배법칙(앞 테이블에만 selection해도 동일)
• π(E1 ∪ E2) = π(E1) ∪ π(E2) : union 분배법칙(projection)

Pushing down selections

selection연산을 가능한 먼저 할 수록 조인되는 릴레이션의 크기가 줄어든다.

• πname, title( σdeptname = "Music"(_Instructor ⋈ (teaches ⋈ πcourseid, title(_course))) )
  => πname, title( σdeptname = "Music"(_Instructor) ⋈ (teaches ⋈ πcourseid, title(_course)) )

: 위 관계대수 식은 Instructor, teaches, course 세 테이블을 조인하여 name과 title을 추출한다. 이때 첫번째 식에서는 teaches와 course를 조인한 결과에 instructor를 조인한 다음 selection연산과 projection을 차례대로 수행하는데, dept_name = "Music"이라는 조건은 Instructor테이블에만 영향을 미치기 때문에 selection을 먼저 수행하면 조인하는 테이블의 크기를 줄일 수 있기 때문에 쿼리의 비용을 줄일 수 있다.

• πname, title( σdeptname = "Music" ^ year = 2017( _Instructor ⋈ (teaches ⋈ πcourseid, title(_course)) )
  => πname, title( σdeptname = "Music" ^ year = 2017(_Instructor ⋈ teaches) ⋈ πcourseid, title(_course) )
  => πname, title( (σdeptname = "Music"(_Instructor) ⋈ σyear = 2017(teaches)) ⋈ πcourseid, title(_course) )

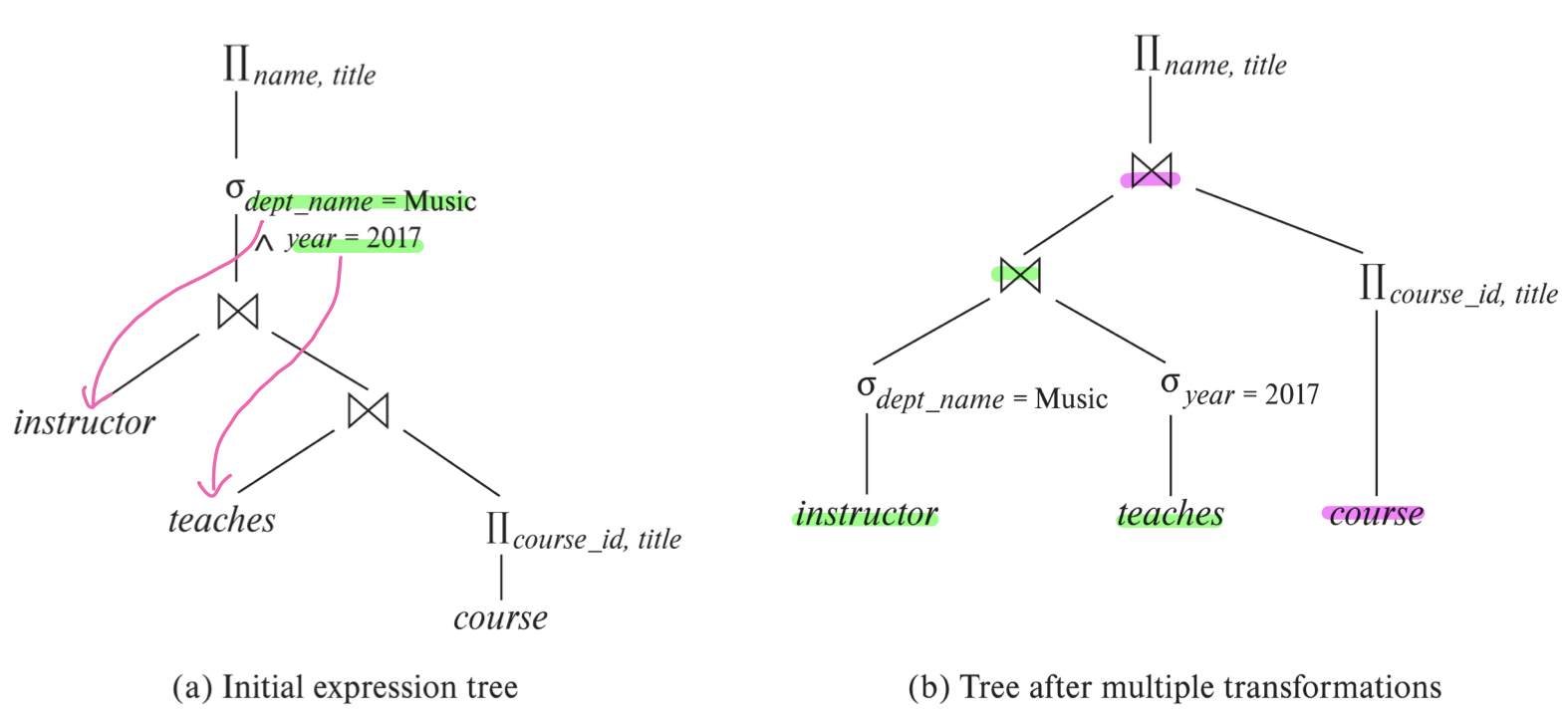
: 위의 쿼리는 앞의 쿼리에서 selection조건이 추가된 것으로, 조인 순서를 변경하고 selection연산을 먼저 수행하는 과정을 통해 중간 결과 테이블의 크기를 줄일 수 있다. 이때, dept_name = "Music"이라는 조건은 Instructor에만 해당하고 year = 2017는 teaches테이블에만 해당하는 조건이기 때문에 selection연산을 분할하면 Instructor와 teaches테이블을 조인하기 전에 selection연산을 수행할 수 있어 비용을 좀 더 줄일 수 있다.

Pushing down projections

projection연산을 가능한 먼저 할 수록 조인되는 릴레이션의 크기가 줄어든다.

• πname, title( (σdeptname = "Music"(_Instructor) ⋈ teaches) ⋈ πcourseid, title(_course) )
  => πname, title( (πname, courseid( (σdept_name = "Music"(_Instructor) ⋈ teaches) ) ⋈ πcourseid, title(_course) )

: 위의 식에서 "σdeptname = "Music"(_Instructor) ⋈ teaches"연산을 수행한 이후 얻는 중간 결과는 (ID, name, dept_name, salary, course_id, sec_id, semester, year) 총 8개의 컬럼을 가지고 있다. 이때 dept_name은 모든 레코드가 Music으로 같고, 최종결과에 포함되는 name과 다음 조인연산에 사용되는 course_id를 제외하면 다른 컬럼들은 필요하지 않다. 따라서 selection이후 πname, course_id 연산을 추가하여 이후 연산에 필요한 값만을 메모리로 올리는 방식으로 쿼리의 비용을 줄일 수 있다.

Join Ordering

조인의 결과로 나오는 릴레이션의 크기가 작은 조인을 먼저 수행한다.

• πname, title( (σdeptname = "Music"(_Instructor) ⋈ (teaches ⋈ πcourseid, title(_course)) )
  => πname, title( (σdeptname = "Music"(_Instructor) ⋈ teaches) ⋈ πcourseid, title(_course) )

: 첫번째 관계대수식은 teaches와 course를 먼저 조인한 다음 selection한 instructor테이블과 조인한다. 그런데 teaches와 course를 조인하면 전체 데이터에 대해 단순히 두 테이블을 조인하는 것이기 때문에 중간 결과의 크기가 더 커지게 되어 비용이 증가하게 된다. 하지만 dept_name = "Music"으로 필터링한 instructor테이블과 teaches를 먼저 조인한다면 필터링 된 데이터에 대해서만 조인이 이루어지기 때문에, 앞의 경우보다 중간결과의 크기가 비교적 작으므로 전체 쿼리의 비용을 줄일 수 있다.

비용추정

쿼리 최적화를의 마지막 단계는 equivalance rule에 따라 만들어 낸 각 evaluation plan에 대해 통계치를 기반으로 비용을 추정하여 가장 적은 비용을 가진 플랜을 선택하는 것이다. 이때 비용추정에 주로 사용되는 통계치는 다음과 같다.

• n : 릴레이션의 튜플의 수(레코드 수)
• b : 릴레이션의 블록 수
• l : 각 튜플의 크기
• f : 블록 당 튜플 수(blocking factor, bf)
• V(A,r) : 릴레이션 r에서 attribute A의 서로 다른 값의 개수
  • ex) V(학년, 학생) = 4 : 학생 테이블에서 학년 컬럼은 1,2,3,4 총 4가지의 값을 가짐
  • πA(r)의 크기와 같음

Selection

Selection 연산결과의 크기는 그 종류에 따라 다음과 같이 추정할 수 있다. 이때 c는 selection 조건을 만족하는 튜플의 수로 정의하여 비용 추정에 사용한다.

1. σA=v(r) : equal 조건
   • c = n / V(A, r) (총 레코드 수 / 서로 다른 값의 수) : 모든 값들이 균등하게 분포한다고 가정한 결과
   • c = 1 if A is key : A가 PK(고유식별자)라면 그 값은 릴레이션에서 유일하기 때문에 selection의 비용은 1이다.
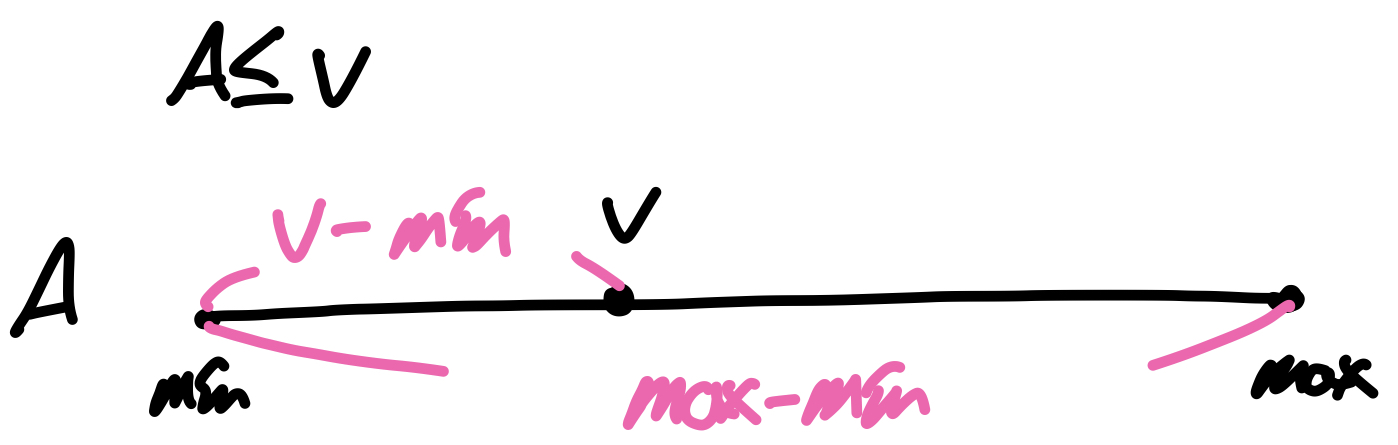
2. σA<=v(r) : range 조건
   • c = 0 if v < min(A,r) : 조건을 만족하는 튜플이 없는 경우
   • c = n * (v-min(A,r) / max(A,r) - min(A,r)) (총 레코드 수 * (조건의 범위 / 전체 범위)) : 릴레이션의 최댓값과 최솟값을 활용하여 조건을 만족하는 레코드의 비율을 계산한 뒤 레코드 수에 곱해 결과의 크기를 추정한다.
   • c = n/2 if absence of statical info : min, max등의 통계자료가 없는 경우 전체 레코드 수의 절반으로 추정한다.

위의 두 조건 이외의 다른 조건들은 여러 조건이 and, or, not으로 연결된 복잡한 조건을 가지기 때문에 selectivity라는 새로운 지표를 정의하여 사용한다.

• selectivity of condition θi : 릴레이션의 튜플 각각이 조건 θi를 만족할 확률
  • selectivity = s / n (조건을 만족하는 레코드의 수 / 전체 레코드의 수)

3. σθ1 ^ θ2 ^ ... ^ θk(r) : Conjunction(and), 각 조건은 독립적이라고 가정(다른 조건에 영향을 주지 않음)
   • c = n (s1s2...sk / n^k) (전체 레코드의 수 * 모든 조건을 만족할 확률) : 모든 조건이 and로 이어진 경우 각 조건의 selectivity를 모두 곱하면 전체 조건을 만족할 확률이 되므로 이를 전체 레코드 수에 곱해 결과의 크기를 추정한다.
4. σθ1 v θ2 v ... v θk : Disjunction(or)
   • c = n (1 - (1 - s1/n)(1-s2/n)...(1-sk/n)) (전체 레코드의 수 * (1 - 모든 조건이 만족하지 않을 확률)) : 모든 조건이 or로 연결된 경우 1에서 각 조건을 만족하지 않을 확률(1-selectivity)을 모두 곱한 값을 빼면 전체 조건 중 하나라도 만족할 확률이 나오므로 이를 전체 레코드 수에 곱해 결과의 크기를 추정할 수 있다.
5. σ¬θ : Negation(not)
   • c = n - size(σθ(r)) (전체 레코드 수 - 조건을 만족하는 레코드 수) : not조건의 결과는 전체 레코드에서 조건을 만족하는 레코드의 수를 빼서 얻을 수 있다.

위의 식을 통해 얻은 c값은 이전 포스팅들에서 다루었던 비용 추정식에 사용하여 최종적으로 연산의 비용을 추정한다. 예를 들어 non-key값에 대한 selection중 집중 인덱스를 사용한 경우 비용식은 Cost = h + b로 나오는데 non-key값에 대한 selection이므로 결과값은 여러개가 나올 수 있고, 집중 인덱스를 사용하므로 결과 튜플들은 모여있다. 따라서 b는 selection의 결과의 크기를 blocking factor로 나누면 계산할 수 있다 (b = ceil(c / bf)). 이와 같이 비용을 추정하기 위해 selection결과의 크기가 필요한 경우 위에서 계산한 c값이 사용된다.

Join

두 테이블 R, S를 조인한 결과의 크기는 join attribute의 종류에 따라 다음과 같이 추정할 수 있다. 이때 R ∩ S 는 두 테이블에 공통으로 존재하는 컬럼의 집합이다.

1. R ∩ S = ø : 두 테이블에서 공통된 컬럼이 없는 경우, 조인연산은 cartesian product와 같다.(r ⋈ s = r x s)
   • c = nr*ns (R의 레코드 수 * S의 레코드 수) : 조인 결과가 cartesian product의 결과와 같기 때문에 두 테이블의 레코드 수의 곱으로 결과의 크기를 구할 수 있다.
2. R ∩ S = key for R : join attribute가 R의 pk인 경우
   • c <= ns : pk에 대한 조인에서 S테이블의 각 튜플은 R테이블에 대해 0개 혹은 1개의 튜플과 조인될 수밖에 없으므로, 조인결과의 레코드 수는 S의 레코드 수를 넘을 수 없다.
3. R ∩ S = foreign key in S referencing R : R테이블의 pk와 S테이블의 fk에 대해 조인하는 경우. RDB에서 대부분의 조인 연산
   • c = ns : S테이블의 fk가 R테이블을 참조하고 있으면 S테이블의 모든 튜플은 R테이블의 정확히 하나의 튜플과 연결되므로, 조인결과의 레코드 수는 S(fk가 있는 테이블)의 레코드 수와 같다.
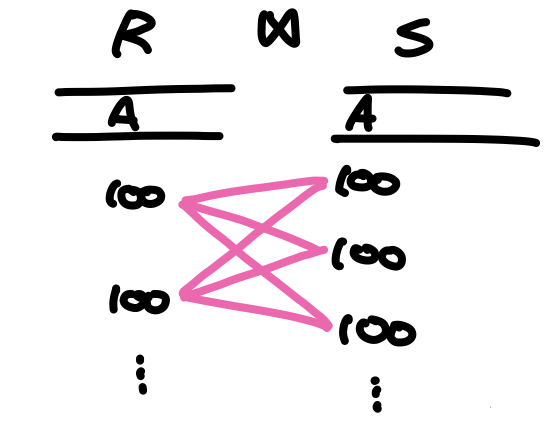
4. R ∩ S = A (not a key for R or S) : join attribute가 키값이 아닌 경우
   • c = min(nr * ns/V(A,s), ns * nr/V(A,r)) : join attritbute가 키값이 아닌 경우 아래 그림과 같이 각 튜플에 대해 조인 쌍이 하나 이상 나올 수 있다. 따라서 각 테이블에 대해서 조인 쌍의 개수를 계산한 뒤 그 중 작은 값으로 조인결과의 크기를 추정한다.
   • 이때 조인 쌍의 개수는 (전체 레코드 수 * 각 튜플에 대응하는 상대 테이블의 레코드 수)로 얻을 수 있고, 상대 테이블의 레코드 수는 σA=v(r)연산의 결과(n / V(A, r))로 추정한다.