이진 탐색은 데이터를 $\log N$만에 찾아주는 매우 편리한 도구죠. 이 포스트에서는 이진 탐색에 대한 내용을 총정리하고, 삼진 탐색보다 이진 탐색이 더 좋은 이유를 수학적으로 증명하겠습니다.

이진 탐색(Binary Search)

이진 탐색은 항상 범위를 반 씩 줄여가며 원하는 수를 찾는 것입니다.

전통적인 예시를 들겠습니다.

당신은 친구와 1부터 100사이 숫자 맞추기 게임을 플레이합니다. 어떤 전략을 써야 할까요? "1이니? 2이니? 3이니?" 이렇게 물어보는 것은 좋지 않은 전략임을 누구나 알 수 있습니다. 이 게임에서 가장 전략적인 방법은 "50보다 크니? (50보다 크다면) 75보다도 크니?" 이런 식으로 물어보는 것임을 단번에 알 수 있습니다.

네, 바로 이렇게 절반씩 덜어내며 원하는 수를 찾는 전략을 이진 탐색이라고 부릅니다.

맞춰야 할 수를 $x$라고 하겠습니다. 이때 변수 ${\rm low}$ 변수 ${\rm high}$를 선언해서 상한과 하한을 정해줍니다. 변수들은 ${\rm low} \le x \le {\rm high}$의 관계를 만족합니다. 이진 탐색은 각 step마다 $x$를 포함하는 반경을 좁혀가며 $x$를 찾습니다. 아래는 $N=101, x=78$일 때의 예시입니다. ($N$이 100이 아니라 101인 이유는 $0$을 포함하기 때문입니다.)

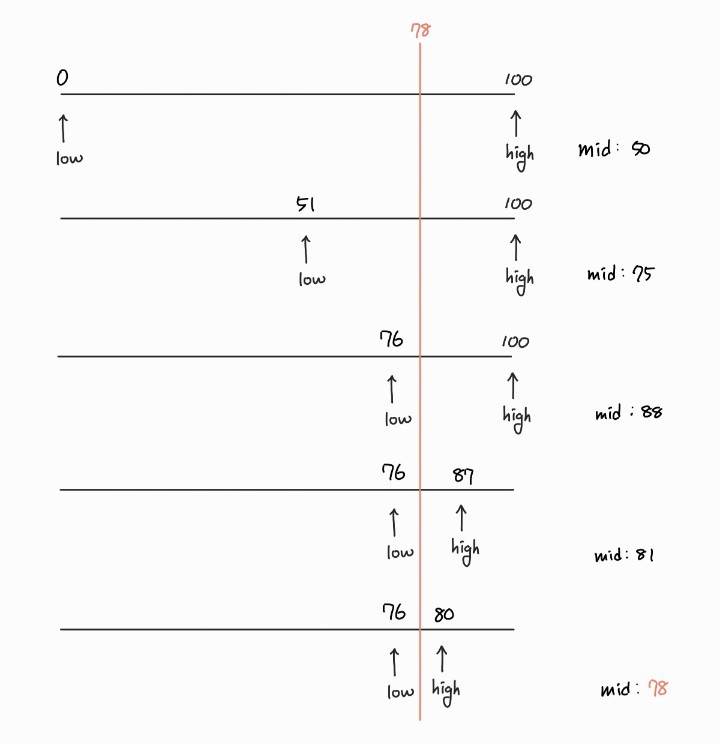
만약 0부터 하나씩 물어보는 순차탐색(sequential search)이었다면 최대 79번 질문을 했어야 할 겁니다. 그런데 이진탐색을 수행하니 5번만에 원하는 값을 찾아내었습니다!

코드

입력: 정수로 이루어진 정렬된 리스트 arr, 찾으려고 하는 값 x
리턴: x 값의 위치(인덱스). x가 존재하지 않으면 -1 리턴

코드 1:

def binary_search(arr, x):
    low = 0
    high = len(arr) - 1
    while low <= high:
        mid = (low + high) // 2
        if arr[mid] == x:
            return mid
        elif arr[mid] > x:
            high = mid - 1
        else:
            low = mid + 1
    return -1

코드 2:

def recursive_binary_search(arr, x):
    if arr == []:return -1
    
    mid = (len(arr) - 1) // 2
    if arr[mid] == x:
        return mid
    elif arr[mid] > x:
        return recursive_binary_search(arr[:mid], x)
    else:
        r = recursive_binary_search(arr[mid + 1:], x)
        if r == -1: return -1
        return r + mid + 1

(사실 코드 2는 배열을 슬라이싱하기 때문에 비효율적이지만, 수학적 귀납법으로 증명하기 위한 연습으로 적어둡니다.)

이 코드의 사용 예는 아래와 같습니다.

arr=[1,3,5,7,9]
print(binary_search(arr, 5))	#output: 2
print(recursive_binary_search(arr, 6))	#output: -1

정확성 증명

코드 1: Proof by Invariant

Invariant는 변하지 않는 성질을 의미합니다. 이 알고리즘에서는 arr[i] = x인 i가 존재한다면 변수들의 관계 low <= i <= high이 변하지 않습니다. (그런 i가 존재하지 않는다면 공허참(Vacuous True)입니다.)

• Invariant low <= i <= high는 최초에 성립합니다. 왜냐하면 초기값으로 low = 0, high = len(arr) - 1을 설정하기 때문입니다. arr에 있는 어떤 값이라도 시작 인덱스 이상, 끝 인덱스 이하에 존재하니까요.
• 코드의 내용 중 그나마 invariant가 깨질 만한 코드는 아래 부분인데

  elif arr[mid] > x:
      high = mid - 1
  else:
      low = mid + 1

  arr가 오름차순으로 정렬된 상태이므로
  • x > arr[mid]라면 mid이하에는 arr[i] = x인 i가 절대로 존재하지 않습니다.
  • x < arr[mid]라면 mid이상에는 arr[i] = x인 i가 절대로 존재하지 않습니다.

즉, invariant는 어떤 상황에도 유지됩니다.

따라서 arr[i] = x인 i가 있다면 loop는 반드시 끝나고 i가 리턴됩니다. low또는 high가 각 step에서 최소 1씩은 반드시 줄어들기 때문입니다.

또한, arr[i] = x인 i가 존재하지 않으면 low <= high의 관계를 유지하다가 어느 순간 low == high인 순간이 오고, 이 때 loop를 한 번 더 돌면 이 관계가 깨짐으로써 -1이 리턴됩니다.

요약

• arr[i] = x인 i가 존재한다면 low <= i <= r 항상 성립 (invariant)
• arr[i] = x인 i가 존재한다면 반드시 i 리턴
• arr[i] = x인 i가 존재하지 않는다면 반드시 -1 리턴

여담으로 구글에 "이분탐색 증명"이라고 검색해서 나온 증명들이 다 김성열 교수님이 수업에서 가르쳐 주셨던 방식이었습니다. 영향력 뭡니까 성열킴...

코드 2: Proof by Induction

수학적 귀납법으로 증명합니다.

• 명제: 어떤 x에 대해 arr[i] = x인 i가 존재한다면 i를 반드시 리턴하고 아니면 -1을 리턴한다.
• Base: $N=0$인 경우, 탐색 범위가 없으므로 즉시 -1이 리턴된다. 성립.
• Step: $N=0,1,2, \cdots,k$일 때, 주어진 명제가 참이라고 가정하자. $N=k+1$일 때,
  • Case 1: arr[mid] == x면 mid를 리턴한다.
  • Case 2: arr[mid] > x면 f(arr[:mid], x)를 호출한다.
    arr[mid] > x이면 mid이상부터는 arr[i] = x인 i를 찾을 수 없다. x를 찾기 위해선 0부터 mid - 1까지 탐색해야하고, $N=0,1,2, \cdots,k$일 때 주어진 명제가 참이라고 했으므로 올바른 답을 리턴한다.
  • Case 3: Case 2와 비슷하다. 그런데, f(arr[mid + 1:], x)이 도출한 답은 축소된 인덱스 범위에서 이루어진 것이므로 mid + 1을 더해서 리턴시킨다. -1이면 더하지 않고 리턴시킴으로써 주어진 명제를 만족한다.
    
    
    
    

시간복잡도

이진탐색은 배열의 길이가 $n$일 때, 최대 $\log n$안에 원하는 수를 찾을 수 있습니다.

증명: 원하는 수를 $\log n$ 안에 찾을 수 있다.

검색은 탐색하는 배열의 크기가 1이 될 때까지 반복됩니다. 매 step마다 중점을 통해서 값을 비교하고 절반씩 날리므로 step의 횟수를 $k$라 하면

$\frac{n}{2^k} = 1$

입니다. 이 수식을 정리하면

$k = \log n$

이진탐색 알고리즘의 시간 복잡도를 $T(n)$이라고 해봅시다. 편의를 위해 $O(1)=1$로 작성하겠습니다. 그러면

입니다. 이 식을 풀면

이 되는데, 위 증명에 의해 $T(1)$에 도달할 때까지 $T$는 $\log n$번 호출되고 $T(1)=1$이므로

$\therefore T(n)=O(\log n)$

삼진탐색(Ternary search)을 안 쓰는 이유

이론적으로 이진 탐색은 $O(\log_2n)$의 성능을, 삼진 탐색은 $O(\log_3n)$의 성능을 갖습니다. 이 경향은 그대로 이어져 10진 탐색은 $O(\log_{10}n)$의 성능을 갖습니다. $k$진 탐색은 $O(\log_kn)$의 성능을 갖는데, $k$가 커지면 커질수록 더 빨라지는 것 아닌가요?

로그의 밑을 명시적으로 표시하면 Big-O 표기법 상으론 빨라지는듯해 보이지만... 결론적으로는 더 느립니다!

로그의 밑변환 공식 $\log_ab = \dfrac{\log_cb}{\log_ca}$을 사용하면 어떤 $k$에 대해 $O(\log_kn)=O(\log n)$이므로 전체적인 성능은 비슷한데 미미한 성능 향상만 보일 뿐이며, 실제로는 $k$진 탐색에서 $k$가 커질수록 Big-O 표기법 $O(\log n)$ 앞에 숨겨진 계수가 더욱 커져서 이진 탐색보다 느려집니다.

이진 탐색의 연산횟수

한 step에서 이진 탐색 코드는 다음과 같이 적힙니다.

if arr[mid] == x: ~
elif arr[mid] > x: ~
else: ~

이때 총 연산 횟수는 2번 입니다.

1. mid가 x의 인덱스인지 확인
2. if ~ else ~로 두 부분 중 어디로 내려가야 하는지 확인

삼진 탐색의 연산횟수

그렇다면 한 step에서 삼진 탐색 코드는 어떻게 적힐까요?

# mid1 < mid2라고 가정
if arr[mid1] == x: ~
elif arr[mid2] == x: ~
elif arr[mid1] > x: ~
elif arr[mid2] < x: ~
else: ~

이때 총 연산 횟수는 4번 입니다.

1. mid1이 x의 인덱스인지 확인
2. mid2이 x의 인덱스인지 확인
3. if로 세 부분 중 가장 왼쪽 부분으로 내려가야 하는지 확인
4. if ~ else ~로 남은 두 부분 중 어디로 내려가야 하는지 확인

$k$진 탐색의 연산 횟수

$k(k>1)$진 탐색은 배열을 $k$개의 부분으로 나누므로 $k-1$개의 mid 변수를 갖고 있습니다. mid 변수들과 x이 일치하는지 확인하는데 $k-1$번의 연산이 필요하게 됩니다.

그리고 어느 부분으로 내려갈지 확인하는 것도 $k$개의 선택지가 있는데, 마지막 부분은 else문을 사용하여 비교연산 1회를 줄일 수 있으므로 역시 $k-1$번의 연산이 필요합니다.

따라서 $k$진 탐색의 한 step에서의 연산 횟수는 총 $2k-2$입니다.

$k$진 탐색의 시간 복잡도

우리는 $k$진 탐색의 한 step에서의 연산 횟수가 $2k-2$라는 것을 계산했습니다. 이것을 바탕으로 시간 복잡도 식을 재귀적으로 작성하면

와 같이 되고, 계산하면

만큼의 시간이 걸리게 됩니다. 함수 $f(k)=\dfrac{2k-2}{\log_2k}$를 $k$에 대해 미분하면

입니다. 부호를 관찰해볼까요?

STEP 1: 분모의 부호

먼저, $k>1$이므로, $f'(k)$의 분모 $\log_2k>0$입니다.

STEP 2: 분자의 부호

$f'(k)$의 분자를 $g(k)$라 할 때, $g'(k)$는

이고, $k>1$일 때, $\left(1-\frac{1}{k}\right)>0$이므로 $g'(k)>0$입니다. 또한, $g(1)=0$이므로 $g(k)>0$입니다.

STEP 3: $f'(k)$의 부호

$k>1$일 때 $f'(k)$의 분자와 분모가 모두 양수입니다. 따라서 $f'(k)>0$이고 이 수식은 $f(k)$가 증가함수임을 말해줍니다.

결론

정리해 봅시다. $k$진 탐색의 시간복잡도는

이고, $f(k)$는 증가함수이므로 $k$가 작을 수록 가장 효율적이고 빠릅니다. 그리고 가능한 가장 작은 $k$의 값은 $2$입니다. 따라서 이진탐색이 가장 효율적입니다!