부동소수점
정의
- 부동(떠다니는) 소수점이라는 의미입니다.
- 컴퓨터는 IEEE 754 표준을 따라 실수를 표현합니다.
- float은 32비트, double은 64비트로 구성됩니다.
구성
부호비트
- 1비트의 크기를 가집니다.
- 실수의 부호를 결정합니다.
- 0을 양수비트, 1을 음수비트로 합니다.
지수부
- float에서는 8비트, double에서는 11비트를 가집니다.
가수부
- float에서는 23비트, double에서는 52비트를 가집니다.
부동소수점 방식으로 실수 표현하기
- 실수 13.8을 부동소수점으로 표현합니다.
정수부
- 십진수 : 13
- 이진수 : 00001101
소수부
-
십진수 : 0.8
-
이진수 : 110011001100....(1100 무한 반복)
2로 곱해서 발생한 carry를 모웁니다.
2로 곱해서 소수점 부분이 0으로 딱 떨어질 때까지 해당 계산을 반복합니다.
0.8 2 = 1.6 ... 1
0.6 2 = 1.2 ... 1
0.2 2 = 0.4 ... 0
0.4 2 = 0.8 ... 0
0.8 2 = 1.6 ... 1
0.6 2 = 1.2 ... 1
0.2 2 = 0.4 ... 0
0.4 2 = 0.8 ... 0
0.8 2 = 1.6 ... 1
0.6 2 = 1.2 ... 1
0.2 2 = 0.4 ... 0
0.4 2 = 0.8 ... 0
.
.
.
(무한 순환소수, 순환마디 1100)
무한 소수, 혹은 엄청 긴 소수점을 가지는 실수는 오차를 낼 수 밖에 없습니다.
아래 부동소수점으로 표현하는 방식을 보면 알 수 있습니다.
-
이진수 : 1101.1100 1100 1100 1100 1100 1100 1100....(13.8)
-
소수점 이동(부동) : 1.1011 1001 1001 1001 1001 1001 1001 ... * 2^3
(소수점을 제일 큰 자리수인 1의 뒤까지 이동합니다.) -
지수부 정규화 :
- 소수점의 이동 칸 수 + bios => 지수부
- 1(0000 0001) + 127(0111 1111) => 128(1000 0000)
-
가수부
- 1011 1001 1001 1001 1001 1001 1001 ......
- 소수점 아래로부터 오른쪽으로 23bit만 사용합니다.
- 1011 1001 1001 1001 1001 100
-
float형에 할당
부호비트 지수부(8bit) 가수부(23bit) 0 1000 0000 1011 1001 1001 1001 1001 100 -
위의 정규화 과정에서 소수점 아래 숫자의 일부가 유실됩니다.
-
예를 들어 어떤 양의 실수를 부동소수점으로 위 과정을 통해 표현하면 소수점을 왼쪽으로 이동시키게 되고, 그로 인해서 원래 정수부에 속하였던 비트들도 가수부로 들어가게 됩니다.
-
그리고 float의 가수부 최대 비트 수(23bit)에 맞춰 들어가면서 나머지 bit는 잘리게 됩니다.
오차가 나면 생기는 일
- 금융, 과학 등 작은 숫자가 중요한 분야에서는 이런 실수의 표현방식으로 나오는 오차가 큰 영향을 끼칩니다.
- 2022년 4월 19일 날짜로 비트코인은 1฿에 50,733,000원 이네요.
가난한 저는 코인을 1฿ 단위로 살 수가 없습니다.
우선 한화로 50,000원을 매수한다고 가정해보겠습니다.
이 돈으로 매수한 코인은 0.00099168฿ 밖에 안되지만... 저에겐 아주 소중합니다.
@Test
public void bitCoinTest(){
double 오만원으로_산_비트코인_개수 = 0.00099168; // 현 시세
double 열아홉배_수익_가즈아 = 오만원으로_산_비트코인_개수 * 19;
double 비트코인_떡락이_두려워_판매한_개수 = 오만원으로_산_비트코인_개수 * 18;
double 남은_비트코인_개수 = 열아홉배_수익_가즈아 - 비트코인_떡락이_두려워_판매한_개수;
Assertions.assertThat(남은_비트코인_개수).isEqualTo(오만원으로_산_비트코인_개수);
}
/*
org.opentest4j.AssertionFailedError:
expected: 9.9168E-4
but was: 9.916799999999983E-4
Expected :9.9168E-4
Actual :9.916799999999983E-4
*/-
위 코드를 보면 증가시킨 만큼 뺏기 때문에 원래 값으로 돌아와야하지만, 아주 작은 오차를 발생시킵니다.
0.00099168(9.9168E-4) <- 계산 전
0.0009916799999999983(9.916799999999983E-4) <-계산 후 -
double(가수부 52bit)의 percision는 float(가수부 23bit)보다 정밀하다해도 이렇게 미묘한 값의 오차를 만드는 것은 다름 없습니다.
-
이는 실수의 표현방식에서 오는 한계이기 때문에 32비트던, 64비트던 오차를 만들 수 밖에 없습니다.
숫자에 민감한 분야는 당연히 float은 사용하면 안되겠고, double을 사용하더라도 rounding rule이 필요할 것으로 생각됩니다. -
다른 방법으로는 BigDecimal Class를 사용하는 것이 있습니다.
BigDecimal
정의
-
위와 같은 정밀도 문제에 대응할 수 있는 java.math 패키지 밑의 클래스 입니다.
-
Java 문서를 보면 다음과 같이 설명되어있습니다.
A BigDecimal consists of an arbitrary precision integer unscaled value and a 32-bit integer scale.
-
위의 내용으로 보면 BigDecimal은 2가지 파트로 구성되어 있음을 알 수 있습니다.
1) arbitrary precision integer unscaled value
2) 32-bit integer scale. -
1)을 해석하자면 "임의의 정밀도를 가지는 정수값"정도가 됩니다.
쉽게 말하면 "임의의 길이를 가지는 정수"라 보면 될 것입니다. -
2)는 32bit 정수값으로 된 "소수점이 찍히는 위치"정도로 이해하시면 되겠습니다.
-
말로만 표현하자니 햇갈릴 것 같아 수식과 예시를 보이겠습니다.
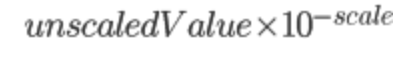
-
이에 대해서 예로 보자면 다음과 같습니다.
4.904894823467456456345 = 4904894823467456456345 * 10^-21
// 정수 * 10^-왼쪽부터 이동한 소수점의 칸 수주의
- BigDecimal class의 생성자는 여러개로 overloading되어있습니다.
- 여기서 주의할 점은 double이나 float을 받는 생성자를 사용할 경우 위 계산식에 의해 오차가 발생한 값으로 BigDecimal 객체가 생성됩니다.
- 코드로 보면 아래와 같습니다.
@Test
@DisplayName("두 BigDecimal 객체를 비교합니다.")
public void towBigDecimalEqualsTest(){
BigDecimal bigDecimalMadeOfFloat = new BigDecimal(0.1289371f);
BigDecimal bigDecimalMadeOfString = new BigDecimal("0.1289371");
Assertions.assertThat(bigDecimalMadeOfFloat).isEqualTo(bigDecimalMadeOfString);;
}
/*
org.opentest4j.AssertionFailedError:
expected: 0.1289371
but was: 0.1289370954036712646484375
Expected :0.1289371
Actual :0.1289370954036712646484375
*/- 같은 0.1289371으로 생성한 것으로 착각할 수 있겠지만, bigDecimalMadeOfFloat의 경우 0.1289371을 32bit 부동소수점으로 변형하면서 근사값으로 표현되고(0.1289370954036712646484375) 이것으로 BigDecimal객체를 생성한 것입니다.
- bigDecimalMadeOfString은 String 내부의 배열을 순회하면서 한 문자씩 가져와 입력한 값(0.1289371)과 같은 BigDecimal객체를 만듭니다.
이에 대한 자세한 동작은 다음에 살펴보도록하겠습니다
결론
- 이번 문서에서는 컴퓨터가 소수를 표현하는 방식, 한계와 문제점, 대안에 대해서 살펴보았습니다.
- 컴퓨터의 실수 계산에 대한 이해가 있어야 개발을 함에 있어 어쩌면 일으킬수도 있는 실수를 피할 수 있고, 발생한 버그에 대한 해결책도 합리적으로 찾을 수 있을 것 같습니다.
