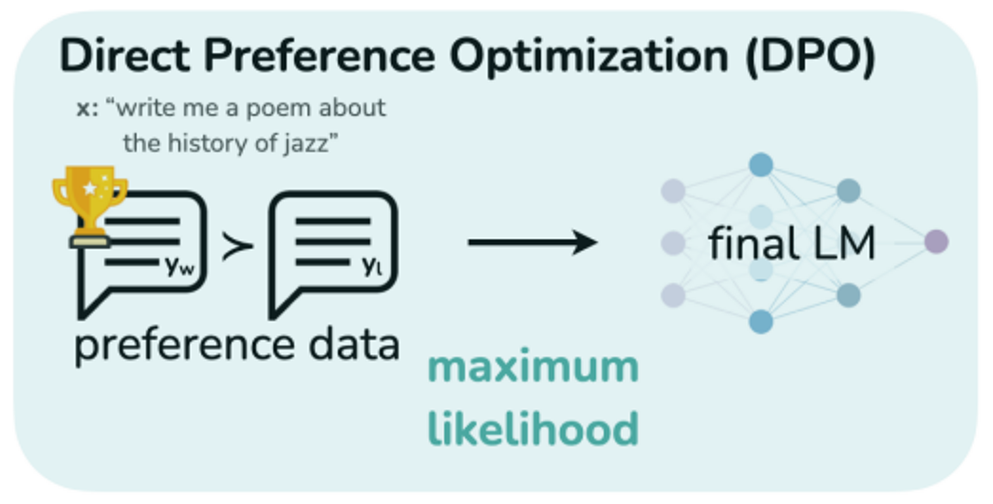
Intro
해당논문 이전까지는 human preference를 높이기위한 방법으로 강화학습을 적용했을때 가장 성공적인 결과가 나왔음
+) RM의 경우 본인이 직접 뭔가 작성하는 것보다 남들이 작성해놓은 것을 보고 평가하는 것이 더 일관성있는 어노테이션이 가능 → 이 rlhf는 최근 llm에 적용되는 방식들은 다 preference데이터를 사용해 답변이 좋으면 좋은 스코어를 주는 형식의 RM 모델 형식으로 만들어 1. SFT, 2. make RM, 3. LM policy 최적화 하는 단계로 진행된다고 생각하면 된다.
Demonstration data 를 많이 만들어서 지도학습으로 finetuning하는 경우 훈련된 annoter라도 차이가 있고 모델입장에서는 annotation품질이 낮은 것도 학습이 진행되는 문제점이 존재함.
DPO : 리워드 모델링 과정 생략 preference 데이터를 directly RM 최적화에 사용하는 방법 제안
reward loss :
πmaxEx∼D,y∼π[r(x,y)]−βDKL[π(y∣x)∥πref(y∣x)]=πmaxEx∼DEy∼π(y∣x)[r(x,y)−βlogπref(y∣x)π(y∣x)]⋯(1)∵DKL=i∑P(i)logP(i)/Q(i)=πminEx∼DEy∼π(y∣x)[logπref(y∣x)π(y∣x)−β1r(x,y)]⋯(2)
(2) 에서는 -1 X 1/ β,
괄호 안에만보면
=log(πref(y∣x)π(y∣x))−log(exp(β1)r(x,y))=log(πref(y∣x)log(exp(β1)r(x,y))π(y∣x))=log(πref(y∣x)log(exp(β1)r(x,y))/Z(x)π(y∣x)/Z(x))=log(πref(y∣x)log(exp(β1)r(x,y))/Z(x)π(y∣x))−logZ(x)
식 정리 그 결과
let)Z(x)=y∑πref(y∣x)exp(1/β×r(x,y))let)π∗(y∣x)=Z(x)1πref(y∣x)exp(β1r(x,y))…(3)
=πminEx∼DEy∼π(y∣x)⎣⎢⎡logZ(x)1πref(y∣x)exp(β1r(x,y))π(y∣x)−logZ(x)⎦⎥⎤
두 개의 정의를 위의 식에 대입하면
=πminEx∼DEy∼π(y∣x)[logπ∗(y∣x)π(y∣x)−logZ(x)]
해당 식을 kl divergence로 정리 할 수 있음,, 왜 Z(x)가 + 로 바뀌는지는 모르겠음,,,
=πminEx∼D(DKL[π(y∣x)∥π∗(y∣x)]+Z(x))…(4)
해당 식 전체를 minimize하는 경우는 KL divergence = 0 인경우, 즉 target의 optim solution ⇒ π∗ 다시 말해 결국 대답이 같아 지는게 optim solution이 된다.
π(y∣x)=π∗(y∣x)=Z(x)1πref(y∣x)exp(β1r(x,y))
4번 수식으로 KL divergence 가 같을 때 loss가 최소이므로 3번식으로 돌아가서 위와같이 쓸 수 있다.
r(x,y) 에 의한 식( reward 함수에 관한 수식으로 변경해주면)
r∗(x,y)=βlogπref(y∣x)π∗(y∣x)Z(x)=βlogπref(y∣x)π∗(y∣x)+βlogZ(x)…(5)
key idea : 로그 확률분포의 비율 (policy 와 ref model ) 이게 의미하는 것은 train our policy, 즉reward function을 의미하게 된다. 또한 같은 의미로 reward 최적화를 만드는 것이므로 human preference를 만족시키게 된다.
B-T (bradley-terry preference model ,1952에 나온 논문)
p∗(y1≻y2∣x)=exp(r∗(x,y1))+exp(r∗(x,y2))exp(r∗(x,y1))…(6)
5번 수식의 최적 reward를 선호도 모델에 대입해 y1> y2 ( y1이 우수한 대답) 을
p∗(y1≻y2∣x)=exp(βlogπref(y1∣x)π∗(y1∣x)+βlogZ(x))+exp(βlogπref(y2∣x)π∗(y2∣x)+βlogZ(x))exp(βlogπref(y1∣x)π∗(y1∣x)+βlogZ(x))=1+exp(βlogπref(y2∣x)π∗(y2∣x)−βlogπref(y1∣x)π∗(y1∣x))1=σ(βlogπref(y1∣x)π∗(y1∣x)−βlogπref(y2∣x)π∗(y2∣x))
맨 위에 식 에서 각 로그를 a,b,c로 각각 치환했을 때 아래와 같이 쉽게 정리할 수 있음
ea+b+ec+bea+b=ea+ecea=1+ec−a1
또한 sigmoid는 1/1+e−x 이기 때문에 σ(a−c) 로 나타낼 수 있다.
마지막,,, 미분
LDPO(πθ;πref)=−E(x,yw,yl)∼D[logσ(βlogπref(yw∣x)πθ(yw∣x)−βlogπref(yl∣x)πθ(yl∣x))]
시그마 안에 부분 (βlogπref(yw∣x)πθ(yw∣x)−βlogπref(yl∣x)πθ(yl∣x)) 을 싹다 u로 치환 후 미분
참고1 : σ′(u)=σ(u)(1−σ(u))
참고2 : 1−σ(u)=σ(−u),
logσ(u)dθdu=σ(u)σ′(u)u′=σ(u)σ(u)(1−σ(u))u′=(1−σ(u))u′=σ(−u)u′
u′은 속미분 결과,,,, (아래와 같이 또 치환) u=r^θ(x,yw)−r^θ(x,yl)
r^θ(x,yw)=βlogπref(yw∣x)πθ(yw∣x),r^θ(x,yl)=βlogπref(yl∣x)πθ(yl∣x),
∇θLDPO(πθ;πref)=−βE(x,yw,yl)∼D[σ(r^θ(x,yl)−r^θ(x,yw))[∇θlogπ(yw∣x)−∇θlogπ(yl∣x)]]
loss 변화의 해석
βE(x,yw,yl)∼Dσ(r^θ(x,yl)−r^θ(x,yw)) : weight by how incorrect the model is
[∇θlogπ(yw∣x)−∇θlogπ(yl∣x)] : increase y_w prob, decrease y_l prob
최종결과
∇θLDPO(πθ;πref)=−∇θE(x,yw,yl)∼D[logσ(βlogπref(yl∣x)πθ(yl∣x)−βlogπref(yw∣x)πθ(yw∣x))]
실험결과
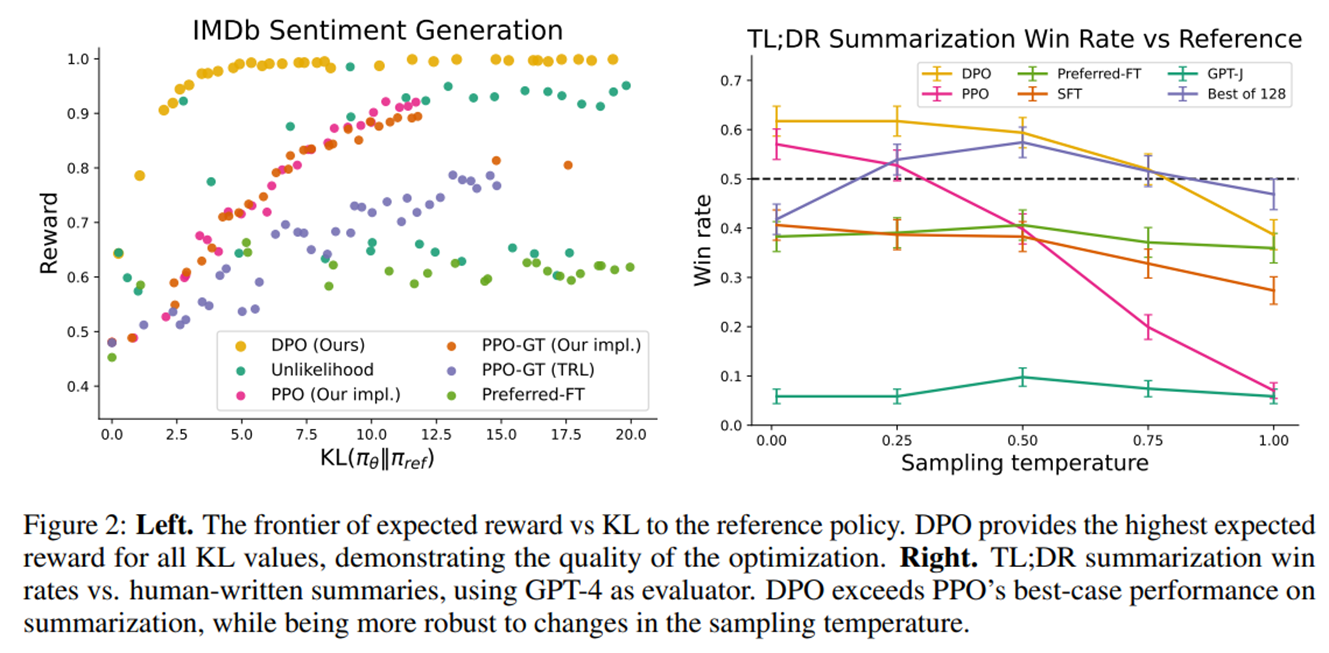
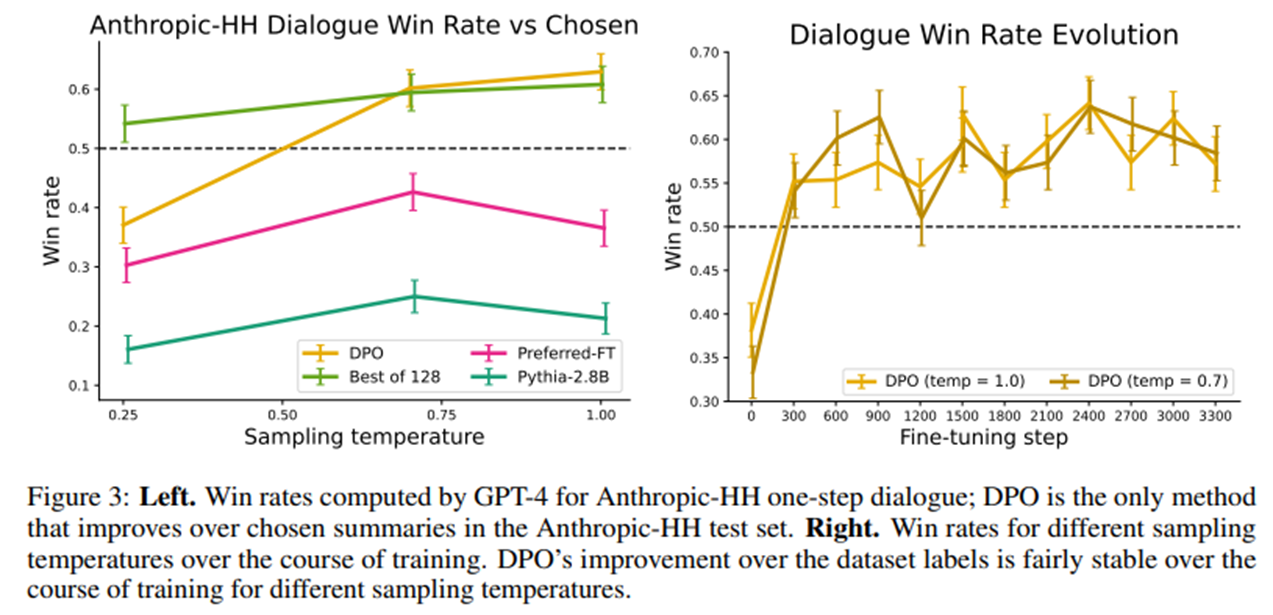
step 증가, KL 증가에 변동성이 적음(ppo에 비해)