- Keyword: dictionary learning, sparse autoencoder
- Novelty: sparse autoencoder scaling law 를 만들어냄.
- Summary: 최적 학습 lr 및 토큰 수, 그리고 새로운 topk sparse autoencoder 방식을 제안함.
- Availability: 세분화된 뉴런 파악, steering
Sparse autoencoders는 sparse bottleneck layer에서 reconstructing activation을 통해 모델 내부 해석가능한 특징을 추출할 수 있는 비지도 학습방식이다. 본 논문에서는 k-sparse autoencoder 방식을 이용해 직접적으로 sparsity를 컨트롤하려한다. 또한 dead latent 를 방지하기 위한 추가적인 방법 또한 제안한다. 본 논문에서는 새로운 평가방식 또한 제안한다. 새로운 평가방식에서 평가를 진행했을 때 autoencoder 사이즈가 증가할 수록 더 좋은 성능이 나타난다는 것을 보였다. (k-sparse: topk 개의 sparsity를 남겨두고 나머지는 0으로 만들어 버린다.)
Sparsity: autoencoder의 latent 의 sparse 하게 표현 (0이 아닌 수로 표현하는 갯수)하는 갯수
이전방식
이전 방식은 small sparse autoencoder를 small language model에만 실험을 진행했다.
본 논문은 다음과 같은 contribution이 있다.
- sparse autoencoder에 대한 sota 학습방식을 소개한다.
- latents의 scale에 대한 scale law를 제안
- latent quality를 평가하기 위한 metric을 제안
Topk activation function
본 논문에서는 k-sparse autoencoder 방식을 사용한다. 해당 방법은 기존 방법에 규제가 없다는 장점이 있다. 식이 아래와 같이 변형된다.
기존 수식: , ,
변형된 수식: ,
다음과 같은 변형은 training loss를 단순한게 표현할 수 있으며 아래와 같은 장점이 있다.
- penalty 제거, 이는 기존에 불완전한 근사화를 시켰던 방식이다. 또한 activation 을 0 으로 축소시키는 bias가 존재했다.
- 직접적인 의 사용으로 빠르게 수렴이 가능한다
- 경험적으로 outperform 한다. (기존 ReLU 방식과 비교했을 때)
- activation이 0으로 수렴하는것을 방지한다.
Preventing dead latents
기존 Claude3 SONA 모델에서 사용한 방식에서는 34M → 12M 만의 latent vector가 살아있는 것이 확인된다고 발표했다. (저자들이 진행했을 때 90%의 dead latent 가 발견되었음). dead latent는 저자들의 방식을 사용했을 때 7%정도가 관찰되었다고 한다.
Scaling Law
1.1 Training to compute-MSE frontier → 훈련 효율성 이해
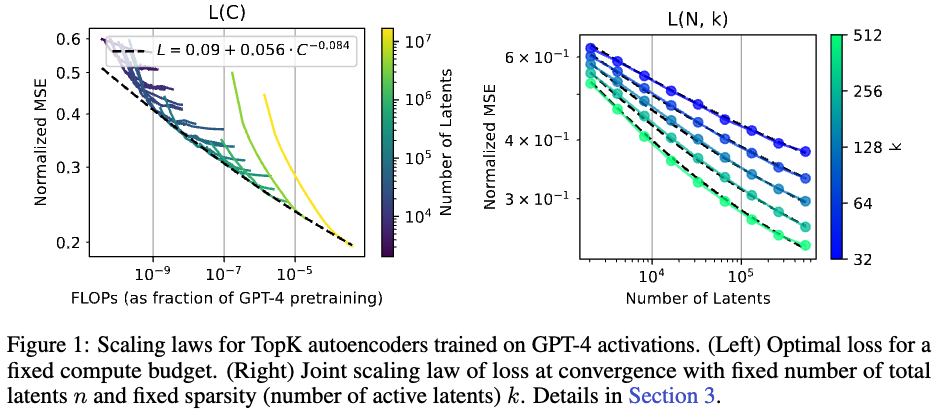
주어진 compute budget 안에서 최적의 MSE를 찾는 과정. (수렴성은 무시)
FLOPs란 Floating Point Operations의 약자로, 초당 수행되는 부동 소수점 연산의 양
오른쪽 그래프 해석: latents 가 증가할 때 FLOPs 는 감소하면서 Loss term 은 감소한다.
1.2 Training to convergence (L(N)) → autoencoder의 사이즈에 따른 최적 error를 찾기 위함
k개의 sparsity가 증가할 수록 에러는 감소하고 이때 모델 사이즈가 증가할 때 error가 감소한다.
1.3 Irreducible loss
scale law에 irreducible loss term 를 넣어준다. 이는 값이 더 지속적으로 향상시키기 위해 사용된다. (0이 되는 것을 방지하기 위함)
1.4 Jointly fitting sparsity →
figure1 (b)를 바탕으로 보면 number of latents 가 증가할 수록 MSE 가 낮아지고 K 값이 커질 수록 MSE 가 낮아지는 것을 볼 수 있다. 본 논문에서는 식을 다음과 같이 제안했다.
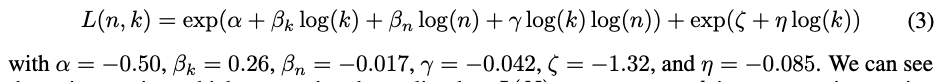
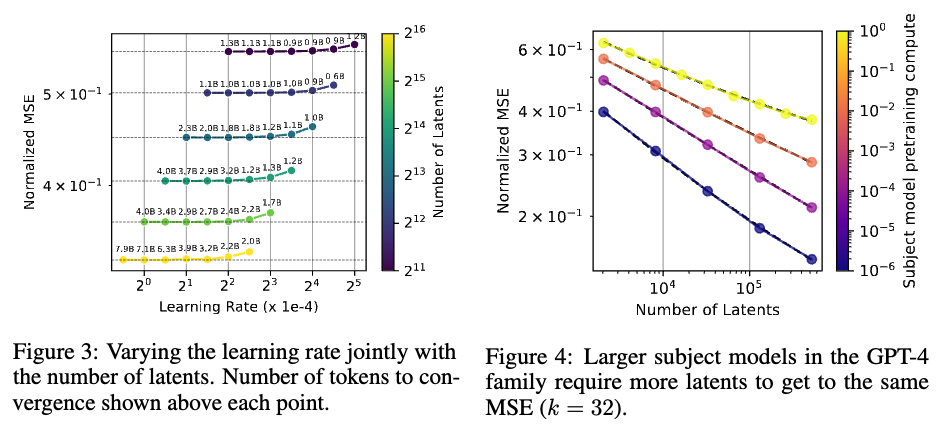
2. Subject model size
figure4 와같이 subject model 사이즈가 증가할 수록 sparse autoencoder 모델의 사이즈가 커져야하는 것을 보여준다.
Evaluation
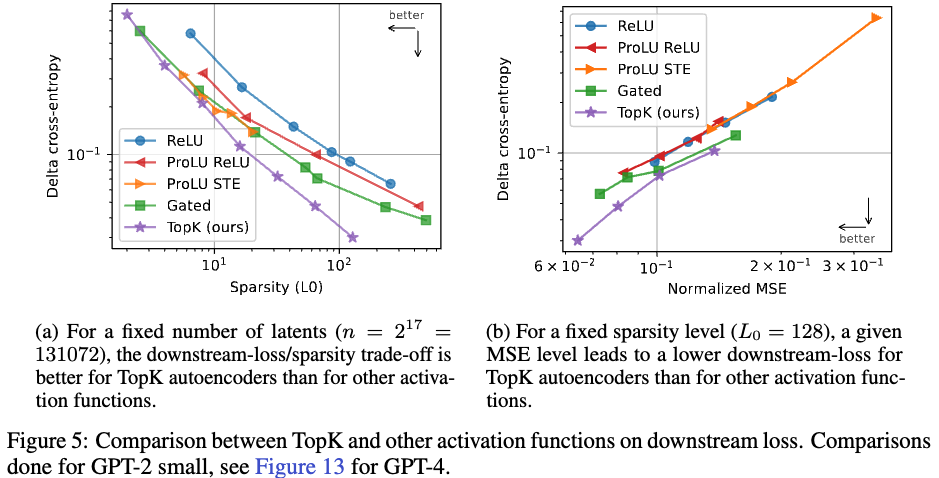
1. Downstream loss
해당 평가 방식은 기존 latent에서 reconstructed latent 로 변경하여 model prediction을 시키는 작업이다.
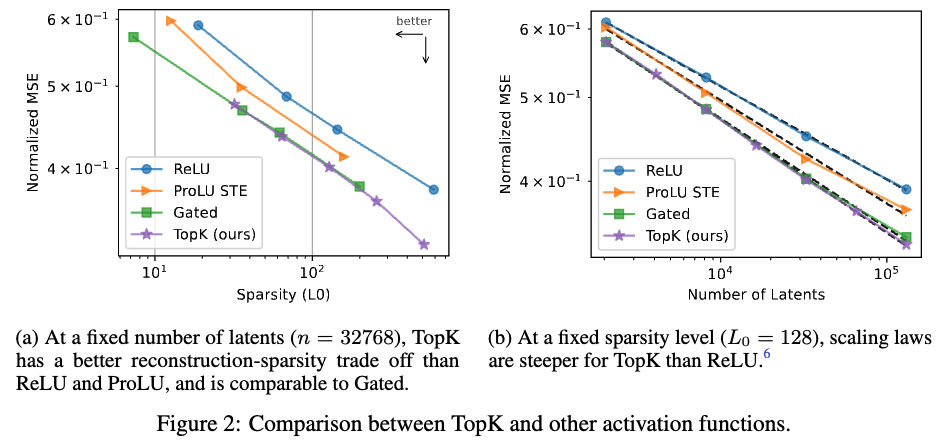
Figure 5에 (a)에 나오듯이 저자들의 방식이 가장 낮은 loss값이 나온다. (a)의 경우 sparsity를 변경하고 latent를 고정시킨 실험이고, (b)의 경우 sparsity를 고정시키고 x,y 축을 각각 MSE, CE 로 본 결과이다.
2. Recovering known features with 1d probes
1d logistic probe를 학습시킨 후 예측에 사용했을 때 단순히 ReLU를 사용했을 때 보다 probe scores가 더 좋게 나온 것을 확인할 수 있었다. 해당 방법은 1 번의 방법보다 상대적으로 computation이 싸다는 장점이 있다. 하지만 해당방법은 features가 자연적으로 존재한다는 가정을 밑바탕으로 깔고 평가가 진행된다는 단점이 있다.
3. Finding simple explanations for features
설명가능한 internal parameter features 를 뽑아내는데는 openai 에서 발표한 방법이 있지만 cost가 너무 크기 때문에 N2G 방법을 사용해 실험을 진행하였다고 한다. 본 논문에서는 기존 ReLU 방식과 비교했을 때 더 precision 이 높게 나왔다고 주장한다.
4. Explanation reconstrction
4.3에서 생성된 설명을 사용해 잠재 차원의 값을 시뮬레이션 진행한다. 이 시뮬레이션도니 값을 실제 값 대신 사용할 때의 다운스트림 손실 값을 측정한다.
이는 모델 해석 가능성과 성능간의 균형을 맞추는데 도움을 준다.
4. Sparsity of ablation effects
잠재 차원을 하나 씩 ablation 할 때 출력 로짓에 미치는 효과의 sparsity를 확인한다. 즉 latent 를 하나씩 0으로 설정하는 것. → 이는 모델 동작을 이해하는데 확실하지만 computation이 많이 필요하다.
Understanding the TopK activation function
1. TopK prevents activation shrinkage
penalty 는 activations들을 0으로 만들어 버린다는 경향성이 존재한다. 본 논문에서 제안하는 TopK activation function은 activation shrinkage 를 방지하는 역할을 한다.
