오늘은 필터의 개념과 종류에 대해 학습할 것이다.
필터란?
필터(Filter)란 영상에서 노이즈를 제거하거나, 이미지에 부드러운 느낌을 주는 것과 같이 원하는 결과를 얻어내기 위해 영상의 픽셀값에 연산을 가해서 새로운 픽셀 값을 얻는 과정을 의미한다.
필터를 사용하는 이유에는 노이즈 제거, Edge 검출, 블러링 등 많은 이유가 있겠지만, 일단 이를 공부하기 전에 Edge가 무엇인지에 대해 먼저 알아보자!
영상에서 사용되는 Edge란?
Edge는 영상에서 밝기나 색상이 급격하게 변하는 부분으로, 명암값이 다른 두 영역 사이에 위치한 경계선을 나타낸다. 이미지에서 Edge를 찾아내는 것은 컴퓨터 비전, 이미지 처리 분야에서 중요하게 여겨지는데, 그 이유는 Edge를 통해 물체의 윤곽선을 식별하고, 이를 기반으로 물체를 인식하거나 분류할 수 있기 때문이다.
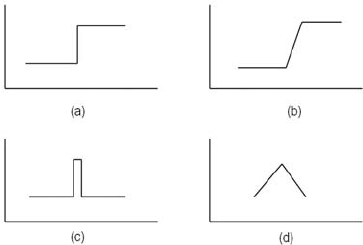
Edge의 종류에는 Step Edge, Ramp Edge, Line Edge, Roof Edge가 있다.
이때, Step Edge는 색상이 급격하게 변화하는 경계를, Line Edge는 색상이 급격히 변했다가 짧은 거리 내에 원래 값으로 다시 되돌아오는 경계를 의미한다.
Step Edge에서 노이즈를 제거하면 Ramp Edge가 되고, Line Edge에서 노이즈를 제거하면 Roof Edge가 된다.
아래의 그림에서 a는 Step Edge를, b는 Ramp Edge를, c는 Line Edge를, d는 Roof Edge를 나타낸다.
이러한 Edge를 검출하는 가장 기본적인 방법은 영상을 (x, y) 변수의 함수로 간주하고, 이를 미분하여 밝기(intensity)의 변화율을 확인하는 것이다. 이때 변화율은 intensity가 변하는 방향과 그 정도를 나타내는 지표로, 값이 급격하게 바뀌는 부분을 의미하기 때문에 이를 통해 Edge를 검출할 수 있다.
Edge를 검출하는 다양한 방법들이 있는데, 이건 Edge Detection의 종류에 대해 알아볼 때 더 자세히 살펴보도록 할 것이다.
필터의 종류
필터의 종류에 대해 알아보기에 앞서, 컨볼루션(Convolution)이 무엇인지 개념을 먼저 알아보자.
컨볼루션이란, 이미지를 필터와 연산하여 새로운 이미지를 생성하는 연산 방법으로, 필터를 통해 정한 특정 범위의 연산을 일정 간격으로 이동해 가며 입력 이미지에 적용하도록 연산하는 것을 의미한다. 따라서 필터를 사용해 원본 이미지에 컨볼루션을 취하면 필터의 특성에 맞게 강조된 이미지를 얻을 수 있다.
사실 이 개념을 알아가면서 너무 깊게 생각하려고 든 부분이 있었던 것 같은데, 쉽게 말해 원본 이미지 위를 이동해 가면서 원본 이미지와 필터의 연산으로 새로운 이미지를 만들어내는 것이 컨볼루션이다.
Spatial Filtering (공간 필터링)
Spatial Filtering은 n*n의 Spatial filter를 만들어 이미지 위를 돌아다니며 연산한 뒤 픽셀 값을 변경해 주는 필터링 방식이다.
그림으로 표현하면 아래의 사진과 같다. 이와 같이 이미지 위를 이동하면서 컨볼루션 연산을 하는 것이 Spatial Filtering이다.
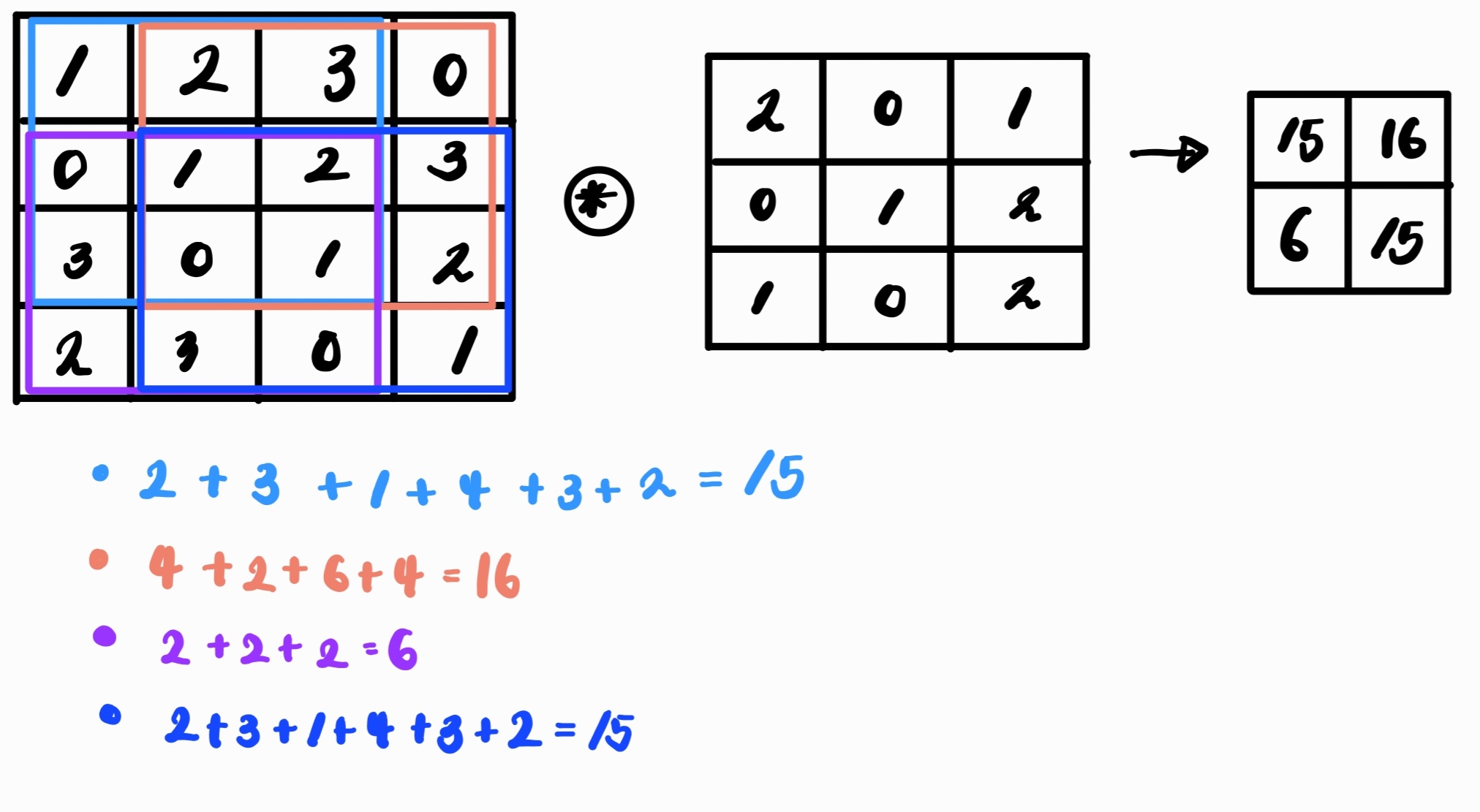
** Spatial Filters = spatial masks, kernels, templates, windows
이들은 이미지 처리에 사용되는 작은 행렬을 의미하며, 각 요소는 가중치를 나타낸다. 모두 같은 의미이니 헷갈리지 않도록 하자.
1) Average Filter
Average Filter는 주어진 픽셀과 그 주변 픽셀의 평균값을 계산하여 해당 픽셀의 값을 변경하는 방식의 필터이다. 이는 특정 픽셀의 값에 주변 픽셀의 값을 포함하게 되기 때문에, 노이즈와 같은 고주파 성분이 분산된다는 성질이 있어 low pass filter 라고도 부른다.
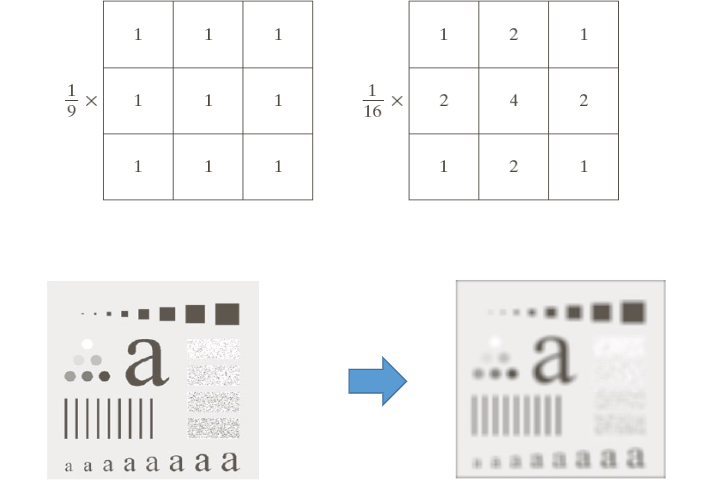
위의 사진을 살펴보자. 첫 번째 필터는 특정 픽셀에 가중치를 두지 않는 방식으로 Average Filter를 수행하고, 두 번째 필터는 가중치 평균을 이용해 Average Filter를 수행한다. 따라서 주변 픽셀보다 중앙 픽셀의 값이 더 강조되는 과정에서 주변의 세부 사항이 더 부드럽게 처리되는 경향이 생기며, 이때 블러링이 발생한다.
- 저주파 성분 : 이미지에서 부드럽고 연속적인 변화가 있는 부분.
즉, 주변 영역과 색 차이가 적은 부분을 의미한다.- 고주파 성분 : 이미지에서 픽셀 값이 급격하게 변하는 부분 (ex) 경계, 선
그렇다면, Averaging Filter를 실제 코드로 표현해 보자.
필자는 말하는 감자 짤을 사용했는데, 실제 실습을 할 땐 본인이 원하는 사진을 사용하면 된다!
import cv2
from google.colab.patches import cv2_imshow
# Mask Size 지정하는데, 이때 크기카 클수록 적용 범위가 커지기 때문에 블러링이 심해진다. 두 가지 서로 다른 크기의 필터를 통해 결과를 확인해 보자!
image = cv2.imread('/content/drive/MyDrive/다운로드.jpg')
filter1 = (5, 5)
filter2 = (30, 30)
averaged_image = cv2.blur(image, filter1)
averaged_image2 = cv2.blur(image, filter2)
cv2_imshow(image)
cv2_imshow(averaged_image)
cv2_imshow(averaged_image2) 결과는 다음과 같다. 픽셀 크기가 커질수록 평균값이 커지고, 이미지도 더 부드러워지기 때문에 블러링 현상이 심해지는 것 또한 확인할 수 있다.
이처럼 Averaging Filter는 노이즈를 효과적으로 줄일 수 있다는 장점이 있지만, 이미지가 부드러워지는 과정에서 세부 정보가 손실되어 블러링이 발생할 수 있다는 단점이 존재한다.
2) Gaussian Filter
Gaussian Filter는 가우시안 분포(Gaussian Distribution)에 근거하여 생성한 가우시안 필터를 사용하는 필터링 기법으로, 중심에 가까운 픽셀에 더 높은 가중치를 준다. 그렇기에 가우시안 분포를 사진 위에 두고 그 위에서 보는 것과 같은 흐릿한 효과를 주는데, 이 때문에 이미지가 더 부드러워지고, Average filter보다 자연스러운 블러링 결과를 생성한다. 이것의 예시를 확인하고 싶다면, 위에서 가중치 평균을 이용해 Average Filter를 수행한 것을 보면 된다.

Gaussian Filter에서 블러링의 정도는 보통 표준편차(σ) 값에 따라 결정되는데, 이 값이 크면 클수록 흩어짐의 정도가 커지기 때문에 이미지의 블러링 정도도 커지게 된다. 따라서 보다 더 선명한 이미지를 얻고 싶다면, 표준편차를 작게 설정해야 한다.
이러한 Gaussian Filter는 주로 이미지를 흐리게 처리할 때나 데이터의 변동성을 줄이기 위한 Smoothing에 사용된다.
그렇다면, 이제 Gaussian Filter를 코드로 한 번 살펴보자.
여기서 중요하게 살펴봐야 할 것은, 표준편차에 따른 블러링 정도 변화이므로 필터 크기는 (5, 5)로 동일하게 두고, 표준편차가 1인 이미지와 5인 이미지로 나누어 살펴보았다.
import cv2
from google.colab.patches import cv2_imshow
image = cv2.imread('/content/drive/MyDrive/다운로드.jpg')
# (이미지, 필터 크기, 표준 편차)
gaussian_filtered_image1 = cv2.GaussianBlur(image, (5, 5), 1)
gaussian_filtered_image2 = cv2.GaussianBlur(image, (5, 5), 5)
cv2_imshow(gaussian_filtered_image1)
cv2_imshow(gaussian_filtered_image2) 코드의 결과를 확인해 보면, 다음과 같이 블러링 정도 차이를 확인할 수 있다.
3) Median Filter
Median Filter는 이름에서도 볼 수 있듯, 필터에서 중앙값을 찾고 픽셀 값을 중앙값으로 대치하는 필터이며, 0과 255와 같이 끝 단에 있는 값을 빼주기 때문에 Salt-and-Pepper noise와 같은 값을 완화해 주는 데 가장 효과적이다.
아래의 사진은 차례대로 Salt-and-Pepper noise가 존재하는 Input, Gaussian Filter를 적용한 이미지, Median Filter를 적용한 이미지이다. Median Filter가 Gaussian Filter보다도 더 효과적인 것을 확인할 수 있다.

이를 코드로 살펴보면 다음과 같다.
커널 크기가 5인 Median Filter를 사용해 이미지를 처리했다.
import cv2
from google.colab.patches import cv2_imshow
image = cv2.imread('/content/drive/MyDrive/Pepper-Noise.png')
median_filtered_image = cv2.medianBlur(image, 5)
cv2_imshow(image)
cv2_imshow(median_filtered_image) 코드 실행 결과 Salt-and-Pepper noise가 효과적으로 제거된 것도도 확인할 수 있다.
추가로, Gaussian Filter를 통해 노이즈를 제거했을 때의 결과는 다음과 같다. 확실히 원본 이미지보다 Salt-and-Pepper noise가 개선된 것을 볼 수 있긴 하나, Median Filter만큼 효과적으로 제거하지 못한다.
이처럼 Median Filter는 Salt-and-Pepper noise와 같이 극단적인 값의 노이즈를 제거하는 데 효과적이라는 장점이 있다. 하지만, 효과가 있는 노이즈 유형이 제한적이라는 단점이 존재한다.
4) Sharpening
Sharpening의 궁극적인 목적은 intensity 값의 변화를 살펴보고, 극적으로 강조하는 것이다. 이렇게 하면 이미지의 Edge나 주요 부분에 포커스를 잡아 이미지를 뚜렷하고 선명하게 나타낼 수 있다.
Sharpening의 방법은 Unsharp Masking을 이용하는 방법과, 2차 미분을 기반으로 하는 방법 이렇게 두 가지로 분류할 수 있는데 일단 더 간단한 Unsharp Masking을 이용하는 방법부터 살펴보자.
이는 원본 이미지에서 블러링된 이미지를 빼서 경계선의 부드러움이 제거된 Unsharp Mask를 만들고, 이를 원본 이미지에 더하여 Edge를 강조하는 방식이다.
각 단계를 표로 표현하면 다음과 같다.
| 단계 | 설명 | 과정 |
|---|---|---|
| Original Signal | 원본 이미지 상태 | 원본 |
| Blurred Signal | 원본 이미지에 블러링 적용 | original + blurring |
| Unsharp Mask | 원본 이미지에서 블러링된 이미지를 뺌으로써 Edge 강조 | original - blurring |
| Sharpened Signal | 원본 이미지에 언샤프 마스크를 더해 선명도를 높인 결과물 | original + unsharp mask |
그리고 이걸 그림으로 확인하면 다음과 같다.
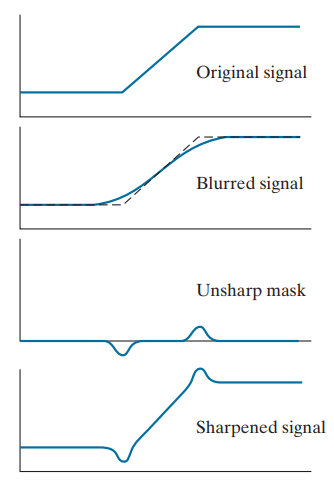
이미지가 블러링되면, 경계 부분이 Smoothing한 결과가 되는데, 원본 이미지에서 이걸 빼게 되면, 이미지의 경계 부분만 남는다. 이를 Unsharp Mask라고 부른다.
이렇게 나온 결과를 원본 이미지에 더해줌으로써 이미지의 경계나 Edge와 같은 주요 부분을 강조하고, 이미지를 선명하게 보여줄 수 있다.
그렇다면, 이제 Unsharp Masking을 이용한 방법을 코드로 살펴보자.
아래의 코드는 위에서 이야기한 과정을 모두 코드로 구현한 것이다.
import cv2
from google.colab.patches import cv2_imshow
image = cv2.imread('/content/drive/MyDrive/다운로드.jpg')
# Blurred Signal = Original Image + blurring
blur = cv2.GaussianBlur(image, (5, 5), 0)
# Unsharp Mask = Original Image - blurring
unsharp = cv2.subtract(image, blur)
# Sharpened Signal = Original Image + Unsharp Mask
Sharpened = cv2.add(image, unsharp)
cv2_imshow(image)
cv2_imshow(Sharpened) 결과를 살펴보면 원본 이미지보다 더 Edge가 강조된 이미지를 확인할 수 있다.
다음으로 미분을 기반으로 하는 Sharpening 방법을 살펴보자. 이는 이미지 경계선에서의 픽셀 변화량(기울기)을 계산하는 방식으로, intensity 변화를 더 잘 보이게 하기 위해 2차 미분을 사용한다.
이해를 위해 Sharpening에서 사용하는 2차 미분을 조금 더 살펴보자.
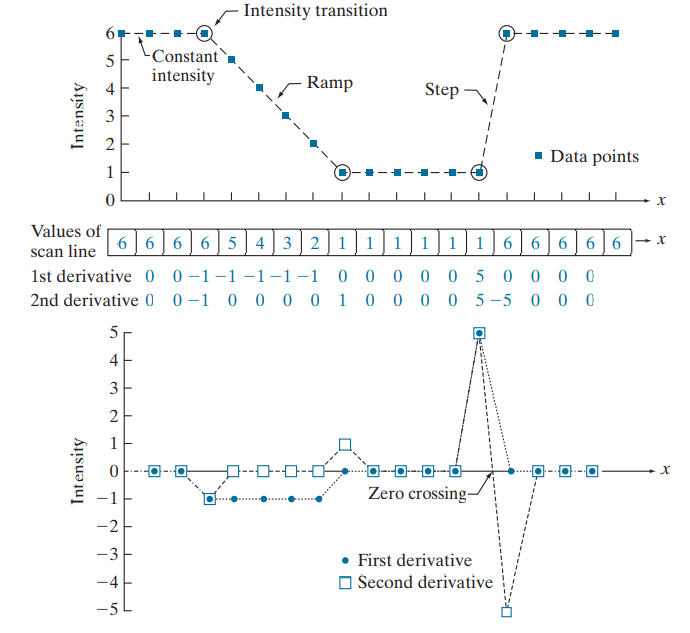
각각의 값들을 표시해둔 것을 Scan line이라 치고, 먼저 1차 미분을 진행한다. 미분이라는 것은 Δy/Δx이기 때문에, Δx=1로, Scan line을 y로 둔 뒤 계산하면 된다.
위 예시로 살펴본다면, (6-6)=0, (6-6)=0, (6-6)=0, (5-6)=-1 이런 순서로 순차적으로 계산해 나가며 값을 결정해 주면 된다.
- peak : 이미지 처리에서 1차 미분은 이미지의 밝기 변화(기울기)를 나타내며, 이때 기울기가 극대값에 도달하는 지점(밝기 변화가 큰 지점, 즉 Edge)을 peak라고 한다.
- zero crossing : 2차 미분은 이미지의 곡률을 나타내며, 이때 미분값이 양수 <-> 음수로 변화하는 구간을 zero crossing라고 한다. zero crossing이 발생하는 구간 사이 0이 되는 지점이 Edge이므로, 이를 통해 Edge의 위치를 식별할 수 있다.
이러한 방식으로 입력 이미지에 대한 2차 미분을 얻고, 입력 이미지에 2차 미분을 더해 주는 것을 2차 미분을 이용한 Sharpening이라고 한다.
그렇다면, 이제 2차 미분이 적용된 마스크를 활용해 Sharpening을 진행하는 과정을 코드로 살펴보자. 이때, 대표적인 2차 미분 필터인 라플라시안 필터를 활용했다.
import cv2
import numpy as np
from google.colab.patches import cv2_imshow
image = cv2.imread('/content/drive/MyDrive/다운로드.jpg')
# 변화를 더 명확히 확인하기 위해 그레이스케일 이미지로 변경했다.
# cv2.cvtColor(img, 색상 공간)을 활용하면 이미지의 색상 공간을 지정할 수 있다.
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
# 2차 미분을 활용한 샤프닝에서는 가중치를 통해 샤프닝 강도를 세밀하게 조절할 수 있다!
# 이 차이가 궁금하다면 alpha 값을 자유롭게 조절해 보면 된다.
alpha = 1.5
# 1. 이미지의 2차 미분 값 구하기
# 라플라시안을 활용할 땐 이미지 픽셀값이 0보다 작거나 255보다 클 수 있기 때문에 출력 이미지의 데이터 타입을 64비트 부동소수점 형식으로 설정해주는 것이 좋다.
laplacian = cv2.Laplacian(gray_image, cv2.CV_64F)
# 2. 2차 미분 값을 원본 이미지에 더하기
# 이때도 마찬가지로 계산 시 이미지의 데이터 타입을 64비트 부동소수점 형식으로 바꾼 뒤 계산해 준다.
sharpened = cv2.add(gray_image.astype(np.float64), alpha * laplacian)
# 최종적으로, 부동소수점 형식으로 계산된 이미지의 픽셀 값을 0~255 범위로 조정한 뒤, 8비트 부호 없는 정수형으로 변환해 준다.
sharpened = np.clip(sharpened, 0, 255).astype(np.uint8)
cv2_imshow(sharpened)코드 실행 결과를 보면 Unsharp Masking을 이용한 방식보다 Edge가 더 강조되는 것을 알 수 있다. 하지만, 이 방식은 Unsharp Masking에 비해 노이즈에 대한 민감도가 크며, 의도하지 않은 이중 에지 효과가 발생할 수도 있다는 단점이 있다.
이때, 이중 에지가 발생하는 이유는 2차 미분을 사용하면 Edge의 시작과 끝에서 부호가 반대인 두 개의 값이 생성되기 때문이다. 이렇게 되면 하나의 Edge에 대해 두 개의 반응(양/음)이 나타나고, 시작점에서의 반응과 끝점에서의 반응이 서로 인접해 있어 마치 두 개의 Edge가 존재하는 것처럼 보인다.
이외에도 Edge Detection에 사용되는 Sobel Filter, Laplacian Filter 등도 Spatial Filtering에 속하는데, 이는 Edge Detection 종류에 대해 다룰 때 더 자세히 살펴보도록 할 것이다.






