버블 정렬

서로 인접한 두 원소를 검사하여 정렬하는 알고리즘

동작 방식

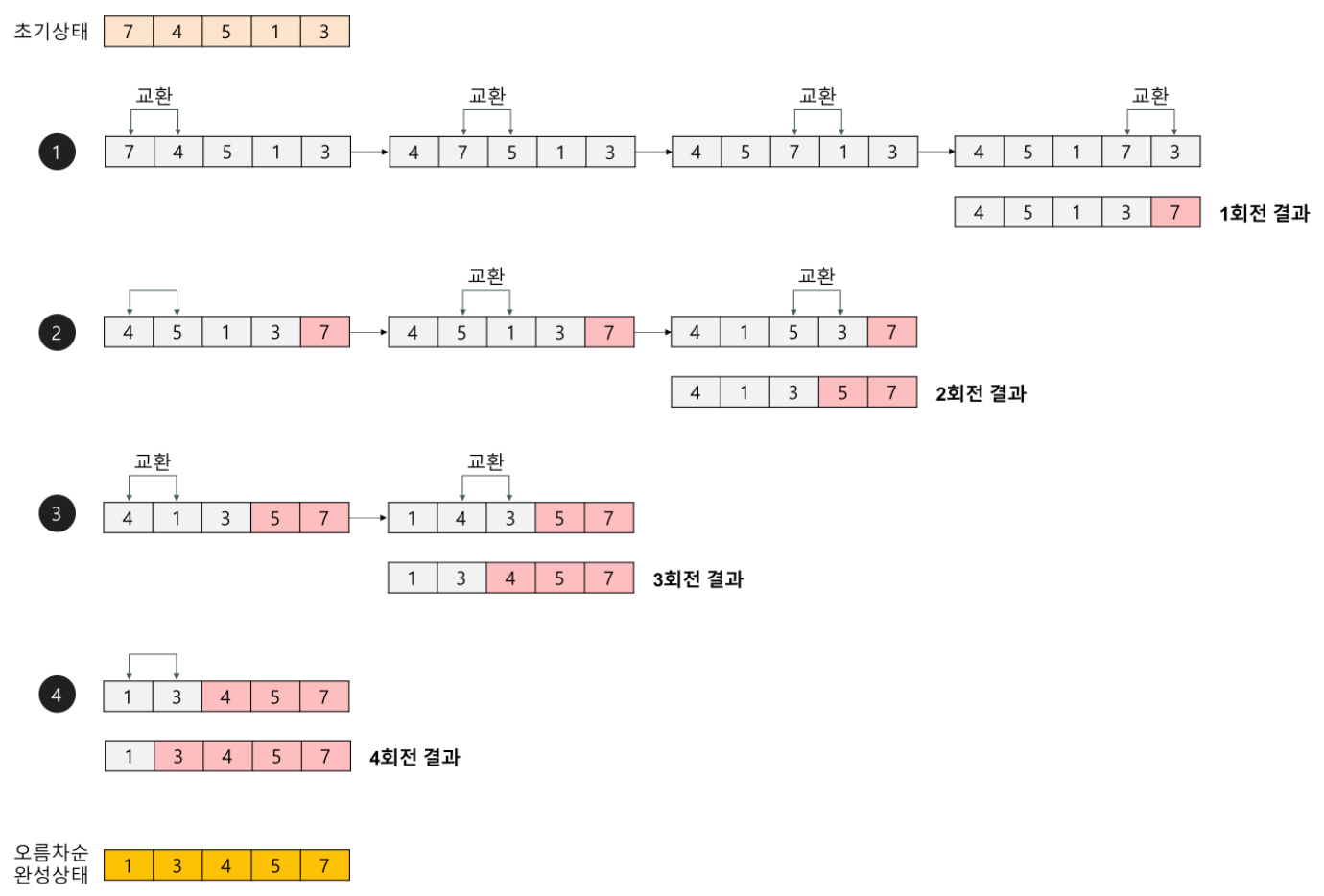
코드

public static void bubbleSort(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        for (int j = 0; j < arr.length - i - 1; j++) {
            if (arr[j] > arr[j+1]) {
                int tmp = arr[j+1];
                arr[j+1] = arr[j];
                arr[j] = tmp;
            }
        }
    }
}

시간 복잡도

O(N^2)

삽입 정렬

이미 정렬된 부분과 비교하여, 자신의 위치를 찾아 삽입하는 방식의 정렬

동작 방식

코드

void insertionSort(int[] list) {
    // 인덱스 0은 이미 정렬된 것으로 본다
    for (int i = 1; i < list.length; i++) {
        key = list[i]; //현재 삽입될 숫자인 i번째 정수를 key 변수로 복사
        
        int j = i - 1;
        
        while (j >= 0 && key < a[j]) {
            a[j+1] = a[j] //이전 원소를 한 칸씩 뒤로 민다.
            j--;
        }
        
        // 반복문 탈출하는 경우 앞으 원소가 타겟보다 작다는 의미다. 
        // 타겟 원소는 j 번째 원소 뒤에 와야 한다. 
        a[j+1] = key;
    }
}
            

시간 복잡도

O(N^2)

병합 정렬

동작 이해

나누는 과정과 합치는 과정으로 이루어져 있다
실제로 정렬이 이루어지는 시점은 2개의 리스트를 합병(merge)하는 단계이다

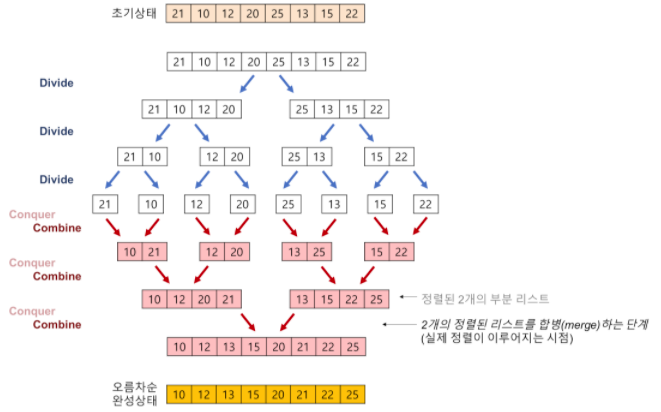
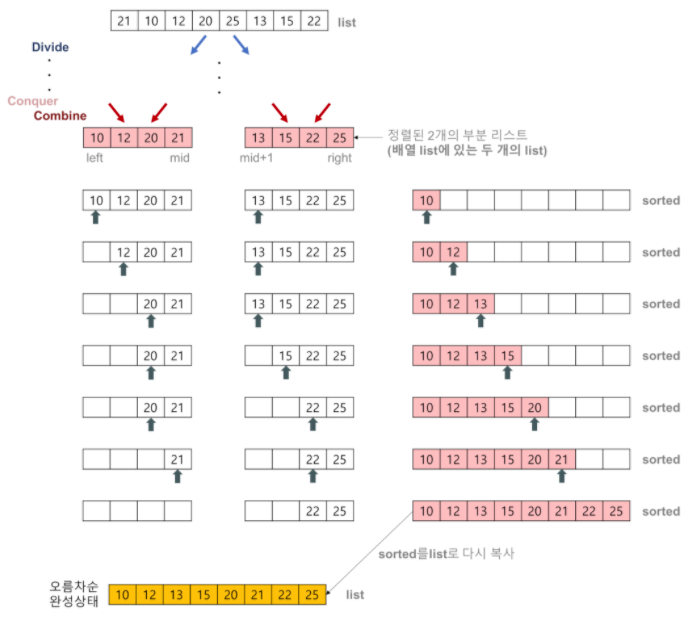
코드

public class test_2 {

    public static void main(String[] args) throws Exception {

        int[] arr = new int[] {1, 3, 5, 7, 9, 2, 4, 6, 8, 10};
        int[] answerArr = new int[arr.length];
        mergeSort(arr, 0, arr.length - 1, answerArr);
        Arrays.stream(arr).forEach(e -> System.out.print(e + " "));
    }

    private static void mergeSort(int[] arr, int l, int r, int[] answerArr) {
        if (l == r)
            return;

        int mid = (l + r) / 2;
        mergeSort(arr, l, mid, answerArr);
        mergeSort(arr, mid + 1, r, answerArr);
        merge(arr, l, mid, r, answerArr);
    }

    private static void merge(int[] arr, int l, int mid, int r, int[] answerArr) {
        int first = l;
        int second = mid + 1;
        int index = l;

        while (first <= mid && second <= r) {
            if (arr[first] < arr[second]) {
                answerArr[index++] = arr[first++];
            } else {
                answerArr[index++] = arr[second++];
            }
        }

        while (first <= mid) {
            answerArr[index++] = arr[first++];
        }

        while (second <= r) {
            answerArr[index++] = arr[second++];
        }

        for (int i = l; i <= r; i++) {
            arr[i] = answerArr[i];
        }
    }
}

성능 분석

병합정렬은 추가적인 메모리를 필요로 한다.

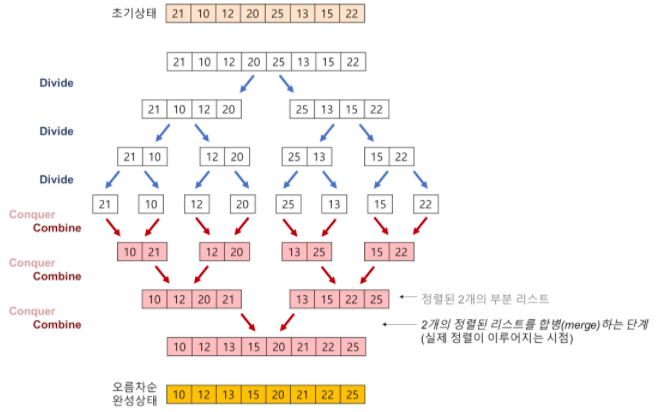
코드를 통해 확인할 수 있다. 데이터를 합치는 부분에서 합치는 크기에 해당하는 임시배열이 필요하다. 즉 위 그림에서 한 행에서 추가적으로 사용하는 메모리들의 합은, 전체 데이터크기에 해당하는 N이다.

시간복잡도는 O(NlogN)이다

• 순환호출 깊이 → $log_2N$

N개의 데이터가 1개가 될 때까지 2등분 하게 된다.

k번 이등분 한다고 생각한다면, 순환 호출의 높이에 해당한다

수식으로 표현하면 아래와 같다

$N \times{\frac12}^k = 1$

$N = 2^k$

$log_2N = k$

• 각 합병단계에서 비교연산 횟수 → N

합병하는 데이터를 모두 옮기는 과정을 거치기 때문에,

한 행에서의 모든 연산횟수를 합하면 N이다.

• 전체 시간복잡도 = 순환호출깊이 x 각 합병단계에서 이동연산 = $nlog_2n$

퀵소트

리스트 안에서 한 요소를 pivot으로 잡고, 피벗을 기준으로 작은 요소들은 왼쪽으로, 큰 요소들은 오른쪽으로 이동 시킨다. 피봇을 기준으로 나뉜 두 부분에 대해 똑같이 반복한다. (재귀)

동작 이해

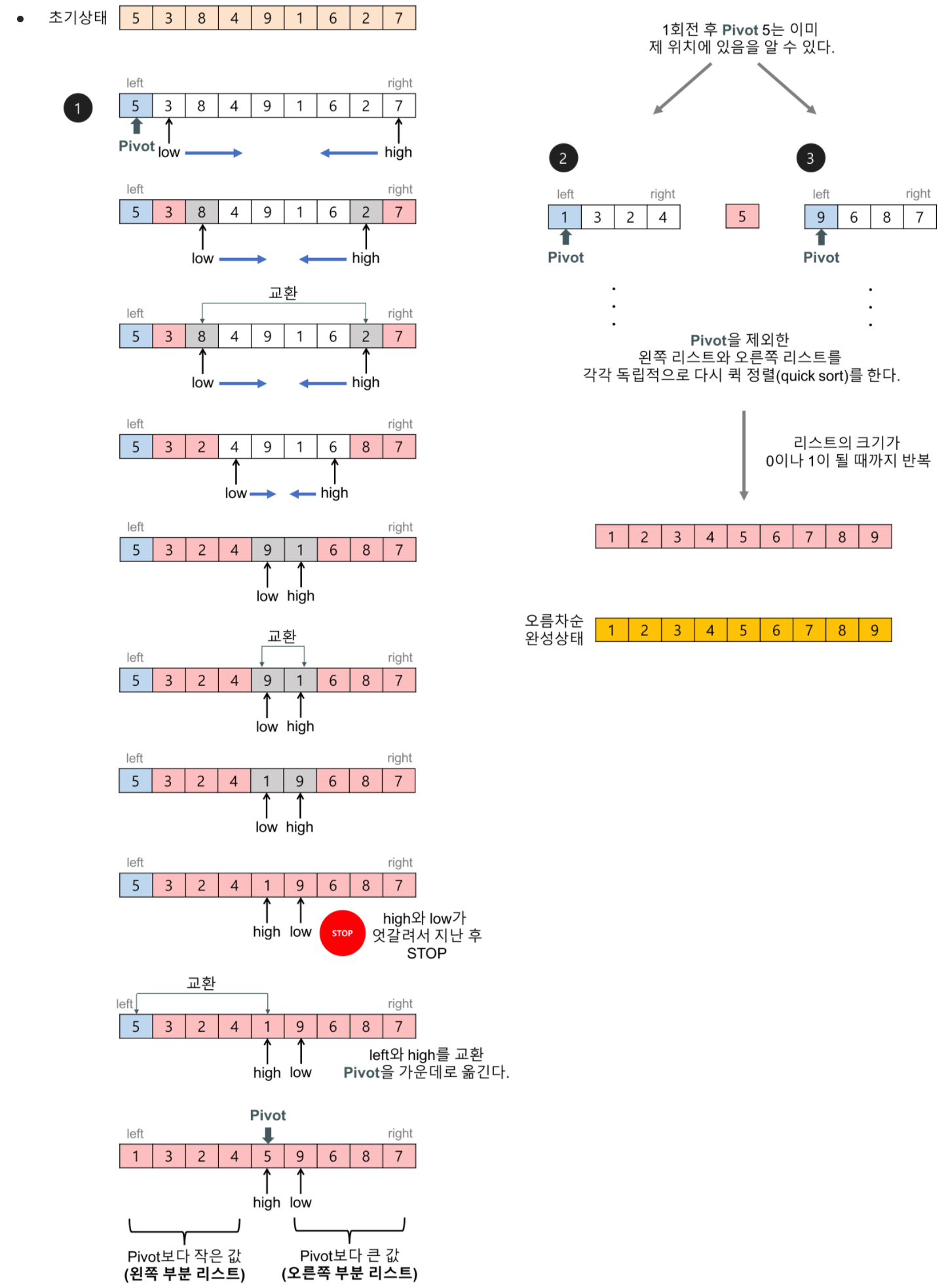
코드

public class QuickSorter {
    public static void quickSort(int[] arr) {
        sort(arr, 0, arr.length - 1);
    }
    
    private static void sort(int[] arr, int low, int high) {
        if (low >= high)
            return;
        
        int pivot = partition(arr, low, high);
        sort(arr, low, pivot - 1);
        sort(arr, pivot + 1, high);
    }
    
    private static int partition(int[] arr, int low, int high) {
        int pivot = arr[left];
        while (low <= high) {
            while (arr[low] < pivot)
                low ++;
            while (arr[high] > privot)
                high --;
            
            if (low <= high) {
                swap(arr, low, high);
                low++;
                high--;
            }
        }
        swap(arr, left, high);
        return high;
    }
    
    private static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        int[i] = arr[j];
        arr[j] = tmp;
    }
}

성능 분석

피벗을 데이터의 중심값으로 계속 정한다면,

정확하게 데이터가 이등분 되면서 재귀호출의 깊이가 $log_2N$ 으로 나올 수 있게 된다.

그러나, 피벗을 계속 한쪽으로 치우친 값으로 정한다면,

순환호출이 깊어질 때 마다 데이터가 1개씩 빠지면서 결국 N깊이가 나오게 된다.

### 시간복잡도 이해: 최선의 경우 → $O(nlogn)$

시간복잡도 이해: 최선의 경우 → O(nlogn)

시간복잡도 이해: 최악의 경우 → O(n^2)

피벗을 계속해서 한쪽으로 쏠린 값을 정한다면 최악의 경우가 된다.
퀵소트의 최악의 경우는 보통 이미 정렬된 배열을 정렬하려 할 때 발생한다

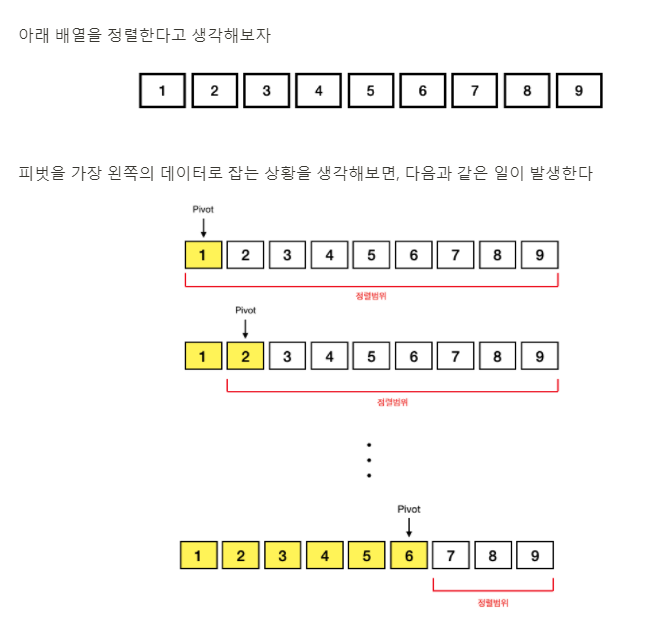
https://www.youtube.com/watch?v=7BDzle2n47c

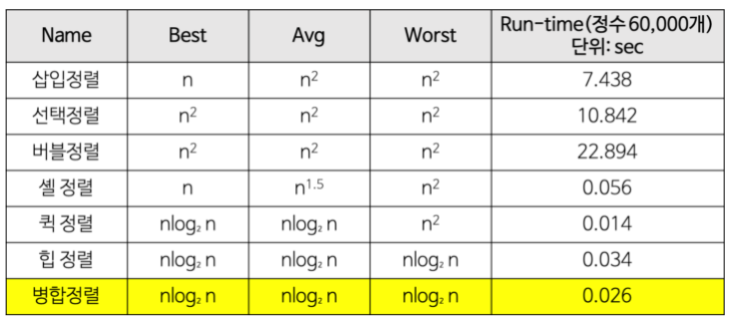
지금까지 정렬 알고리즘 분석

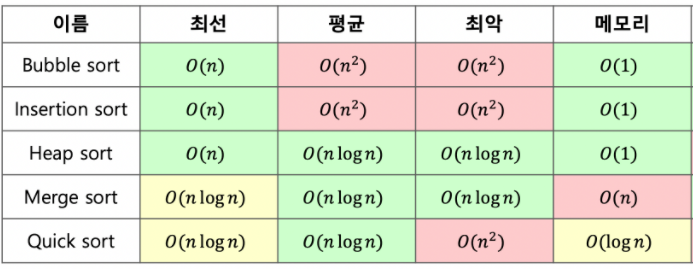
quick sort

시간복잡도가, 왜 최악의 경우 $O(N^2)$ 일까?

Pivot 을 계속해서 치우친 값으로 잡게 되면,
재귀호출의 깊이가 N으로 깊어지게 된다.
동일한 재귀호출 깊이에서의 모든 연산은 O(N)이고
이것을 N번 반복하므로, 결과적으로 $O(N^2)$이다.

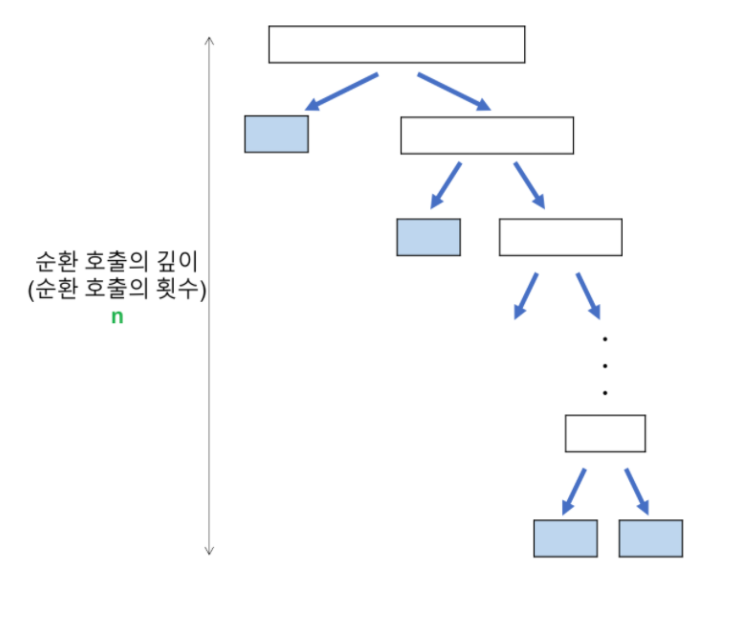
공간복잡도가 $O(logn)$일까?

→ 재귀호출의 깊이가 logn 이기 때문에, logn에 해당하는 스택메모리가 추가로 필요하다
quick sort는 데이터를 이등분 하면서 재귀적으로 실행된다.
이때 재귀호출의 깊이는 "데이터 갯수가 1이 될 때까지 2등분하는 횟수" 이다.
따라서, $log_2n$번의 순환호출을 하게 된다.
즉, 스택을 통해 $log_2n$ 개의 메모리공간을 할당해야한다는 의미이므로, $O(log_2N)$ 이 된다.

merge sort

왜 공간복잡도가 $O(N)$일까?

merge 하는 과정에서 임시적으로 데이터를 담아둘 공간이 필요하다.
동일한 재귀호출 깊이에서 필요한 모든 데이터공간은 N이기 때문에,
필요한 추가메모리가 O(N)이 된다.

Heap Sort

heap sort는 왜 quick sort, merge sort에 비해서 조금 느릴까?

→ https://d2.naver.com/helloworld/0315536 참고

팀소트

분할을 해서 작은 부분에 대해서는 insertion sort를 사용하고 전체적으로 mergesort 방식을 채택한 것이다. insertion sort를 사용하는 이유는 지역 참조성이 좋기 때문이다.

https://d2.naver.com/helloworld/0315536

기타

자바에서 sort

Arrays.sort()

먼저 배열을 정렬하는 Arrays.sort에 대해서 알아보도록 하겠습니다. Arrays.sort의 코드를 확인했을 때 아래와 같이 주석과 코드가 나왔습니다. 이를 통해서 보면 듀얼피봇 퀵정렬(Dual-Pivot QuickSort)를 사용한다고 명시되어있는 것을 확인할 수 있었습니다. 듀얼피봇 퀵정렬은 일반적인 퀵정렬과는 다르게 피봇을 2개를 두고 3개의 구간을 만들어 퀵정렬을 진행한다고 합니다. 이 정렬방식은 랜덤 데이터에 대해서 평균적으로 퀵소트 보다 좋은 성능을 낸다고 알려져있습니다.
https://sabarada.tistory.com/138

Collections.sort

레거시로 합병정렬과 Tim 정렬을 사용하고 있다는 사실을 알 수 있었습니다. Tim 정렬은 삽입(Insertion) 정렬과 합병(Merge) 정렬을 결합하여 만든 정렬이라고 합니다. 그리고 Java 7부터 Tim 정렬을 채택하여 사용하고 있다고 합니다.

Arrays.sort() VS Collections.sort()

그렇다면 Arrays를 정렬했을때와 Collections를 정렬했을때 왜 사용하는 알고리즘이 다른걸까요 ? 그 이유는 바로 참조 지역성 원리(Local of Reference)에 있습니다. 참조 지역성의 원리란 동일한 값 또는 해당 값의 근처에 있는 스토리지 위치가 자주 액세스되는 특성을 말합니다. 이 참조 지역성의 원리는 CPU의 캐싱 전략에 영항을 미칩니다. 즉, CPU가 데이터를 엑세스하며 해당 데이터만이 아니라 인접한 메모리에 있는 데이터 또한 캐시 메모리에 함께 올려둡니다.

정렬의 실제 동작 시간은 C * 시간복잡도 + a라고 합니다. 시간복잡도는 다 아시는 내용일 것이고 a 상대적으로 무시할 수 있습니다. 하지만 곱해지는 C의 영향도는 고려를 해야합니다. 생각하지 않을 수 없습니다. 이 C라는 값이 바로 참조 지역성 원리가 영향을 미칩니다.

Array는 메모리적으로 각 값들이 연속적인 주소를 가지고 있기 때문에 C의 값이 낮습니다. 그래서 참조 지역성이 좋은 퀵 정렬을 이용하면 충분한 성능을 제공할 수 있다고 합니다. 하지만 Collection은 List를 기준으로 봤을때 메모리간 인접한 ArrayList 뿐만 아니라 메모리적으로 산발적인 LinkedList도 함께 존재합니다. 따라서 참조 인접성이 좋지 않고 C의 값이 상대적으로 높다고 합니다. 이럴 때는 퀵 정렬 보다는 합병정렬과 삽입정렬을 병합한 Tim 정렬을 이용하는게 평균적으로 더 좋은 성능을 기대할 수 있다고합니다.

머지소트와 퀵소트를 비교해주세요

퀵소트

퀵소트는 2 단계로 이루어져 있다.
첫번째로, 정렬범위에서 피벗을 정해서 피벗 왼쪽엔 피벗보다 작은 숫자들을, 오른쪽엔 큰 숫자들을 배치시킨다. 이때의 총 연산횟수는 N번이다.
두번째로, 각각의 범위에 재귀적으로 다시 첫번째 단계를 적용한다.
이때, 동일한 순환호출단계의 모든 데이터범위에 첫번째 단계를 적용할때, 모든 비교연산횟수를 더하더라도 N번이다.
따라서 피벗을 통해 최대한 정렬범위를 반씩 나눠 순환호출의 깊이를 작게 하는것이 중요하다.
피벗을 계속해서 정렬범위의 중앙데이터로 정한다면, logN번만에 모든 정렬범위를 1로 만들 수 있고, 각각의 순환호출 단계의 총연산이 N이기 때문에, 정렬성능은 NlogN이다.

머지소트

머지소트는 데이터의 중앙을 기준으로 데이터를 반으로 나눈다.
범위가 1이 될 때까지 재귀적으로 반복된다.
그리고 나눠진 각각의 범위를 합치면서 정렬하게 되는데, 이때 동일한 순환호출단계의 모든연산횟수는 O(N)이다.
머지소트는 데이터를 정확히 반으로 나누기 때문에, 순환호출의 깊이는 logN이 보장되며, 따라서 전체 성능은 NlogN이다.

비교

퀵소트는 정렬하는데 있어 추가적인 공간을 거의 필요로 하지 않는다. 그러나 머지소트는 데이터범위를 합칠때 임시배열에 해당 데이터를 담아야 하기 때문에 O(N)의 추가데이터가 필요하다.
퀵소트는 또한 캐시지역성을 최대한 활용한다고 알려져 있다.

캐시 로컬리티 측면에서 비교

https://medium.com/pocs/locality%EC%9D%98-%EA%B4%80%EC%A0%90%EC%97%90%EC%84%9C-quick-sort%EA%B0%80-merge-sort%EB%B3%B4%EB%8B%A4-%EB%B9%A0%EB%A5%B8-%EC%9D%B4%EC%9C%A0-824798181693
결론: 퀵소트는 메모리 조회가 넓은 범위로 이루어지지 않는다. 재귀적으로 정렬을 실행하지만, 순차적인 범위를 정렬한다. 하지만 머지소트는 메모리조회가 처음과 끝을 계속해서 반복하며 오간다. 따라서 캐시지역성을 활용하는 것이 퀵소트보다 힘들다. 이는 빅오노테이션에서 상수 (A*NlogN + B) 에서 A와 B 부분등의 상수값을 증가시키는 요인으로 작용하고, 따라서 평균적으로 퀵소트보다 성능이 좋지 않다고 알려져 있다.