Day 1
Performance Measures
For
now, we shall measure the amount of effort to solve a linear programming problem by counting the number of iterations, i.e., pivots, needed to solve it.

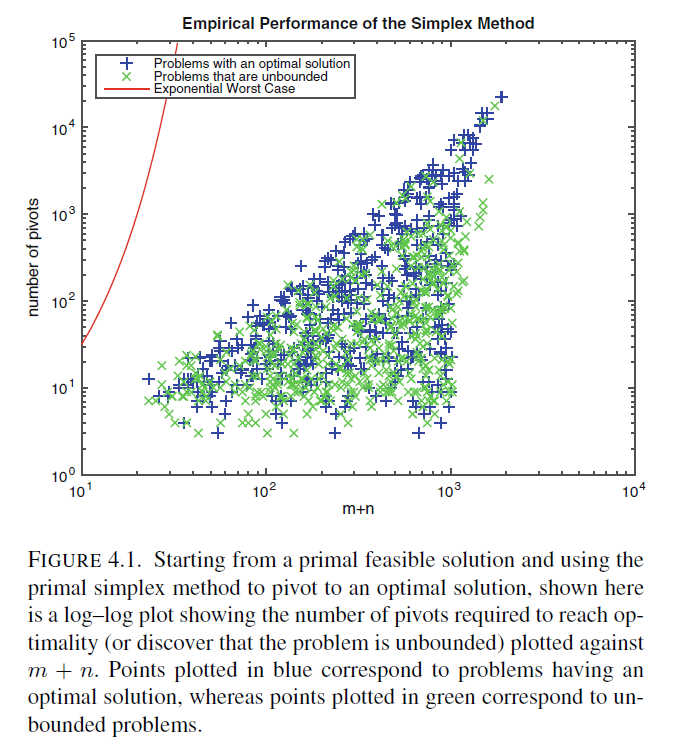
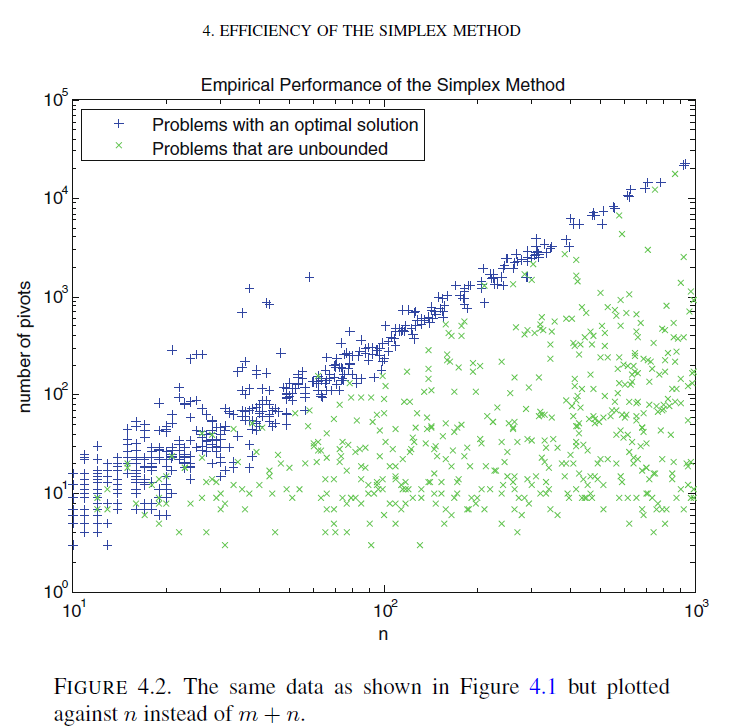
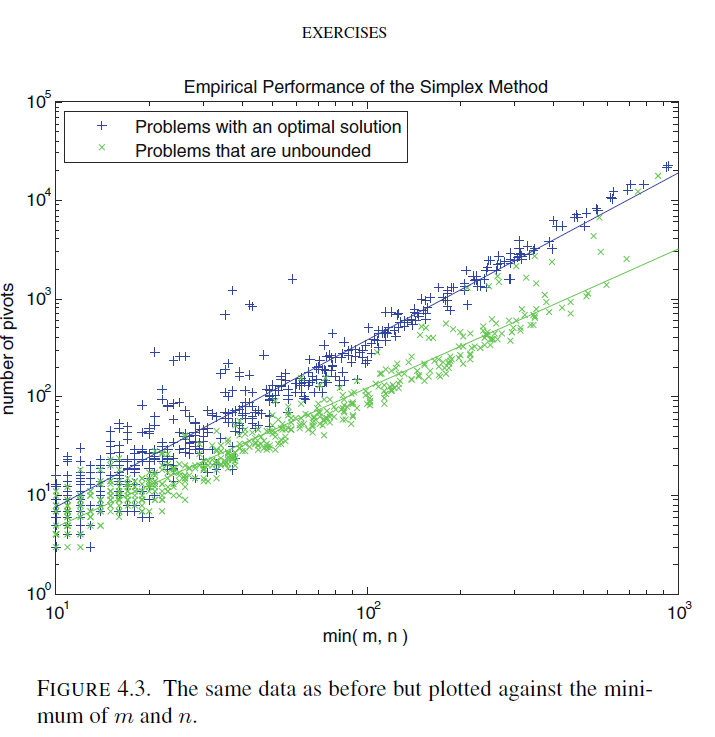
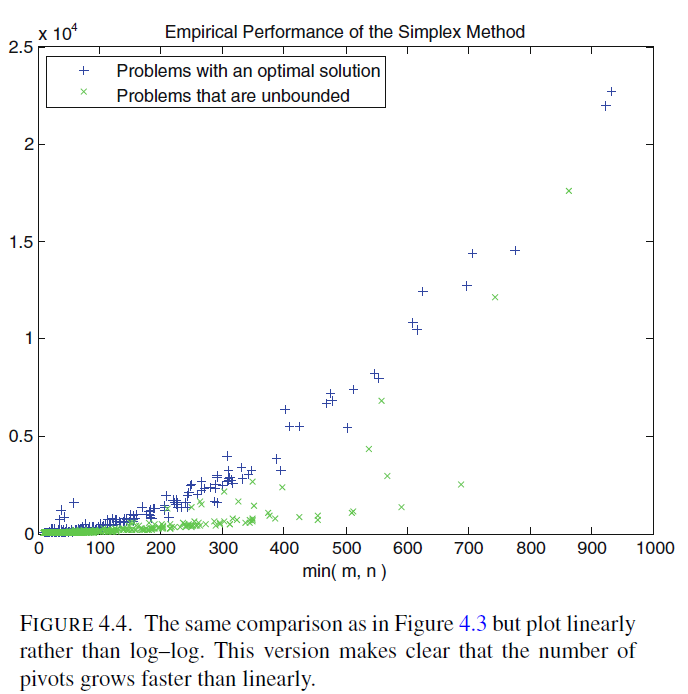
Day 2
p.59
Duality Theory
It turns out that every feasible solution for one of these two linear programs gives a bound on the optimal objective function value for the other.
Associated with every linaer programming is another called its dual.
We begin with an example,
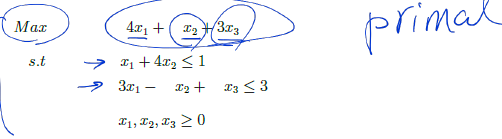
Every faseible solution provides a lower bound on the optimal objective function.
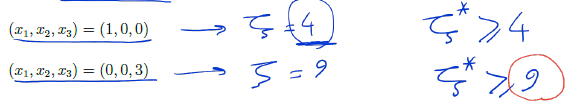
Let's multiply the first constraint by 2 and add that to the 3 times the second constraint,
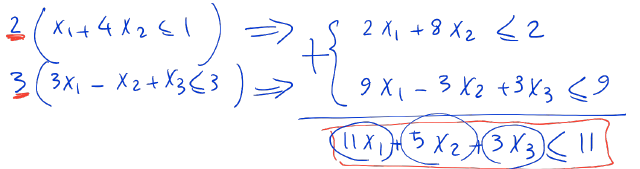
Since every variable is nonnegative, we can compare the sum against the objective function and notice that,
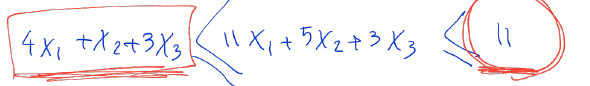
To get a better upper bound, we apply the same boundig technique, but we start by multiplying the constraints by nonnegative variables y1 and y2, respectively.
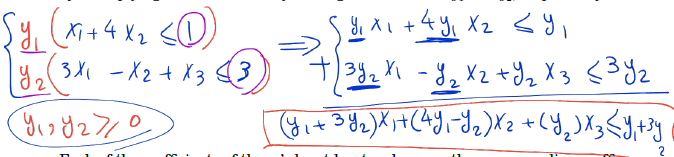
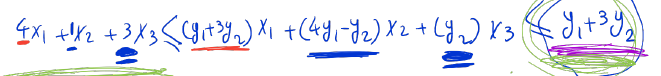
If we stipulate that each of the coefficients of the xi’s be at least as large as the corresponding coefficient in the objective function,v
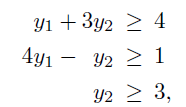
Then we compare the objective function against the sum,
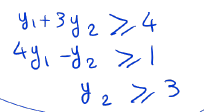
We now have an upper bound which should be minimized to obtain the best upper bound. We are led to the following opmization problem which is called the dual linear programming problem associated with the original linaer programming problem.
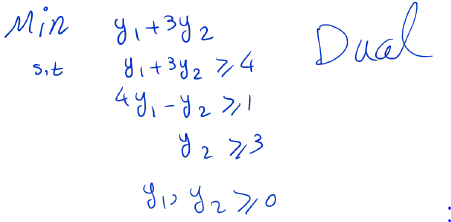
This problem is called the dual linear programming problem associated with the given linear programming problem. In the next section, we will define the dual linear programming problem in general.
The Dual Problem
Given a linear programming problem in standard form,
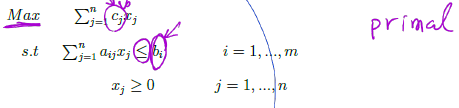
the associated dual linear program is given by
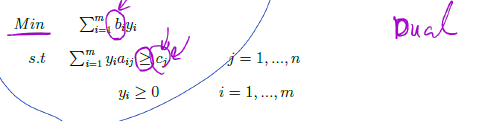
Our first order of business is to show that taking the dual of the dual returns us to the primal. To see this, we first must write the dual problem in standard form. That is, we must change the minimization into a maximization and we must change the first set of greater-than-orequal-to constraints into less-than-or-equal-to. Of course, we must make these changes
without altering the problem. To change a minimization into a maximization, we note that to minimize something it is equivalent to maximize its negative and then negate the answer:
Example

In order to get the standard form of the dual problem we need to change the minimization to maximization and the direction of the inequality.

The standard form of the dual problem is

Day 3
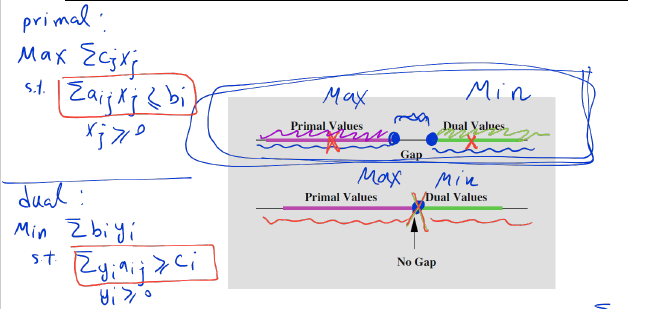
The weak Duality Theorem
p.60
As we saw in our example, the dual problem provides upper bounds for the primal objective function value. This result is true in general and is referred to as the weak duality theorem:
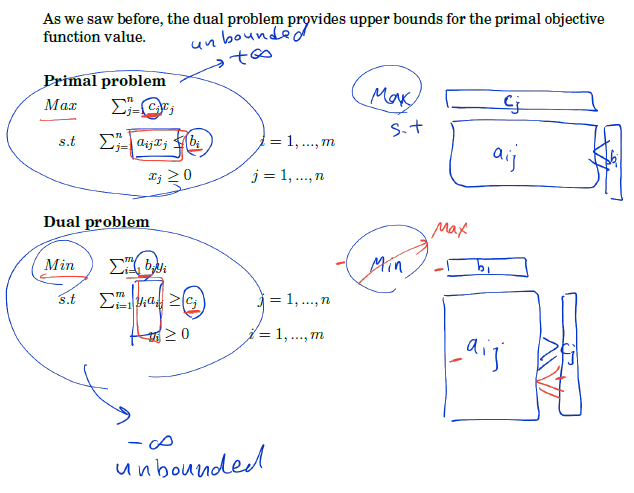
Theorem 5.1: THEOREM 5.1. If (x1, x2, . . . , xn) is feasible for the primal and (y1, y2, . . . , ym) is feasible for the dual, then

바로 위에 보면 bi가 aij xj sum 보다 큰 것이 나와있다.

The Strong Duality Theorem
The fact that for linear programming there is never a gap between the primal and the dual optimal objective values is usually referred to as the strong duality theorem:
Theroem 5.2
"an"을 집중해서 봐야한다.
Example (Lecture Note)
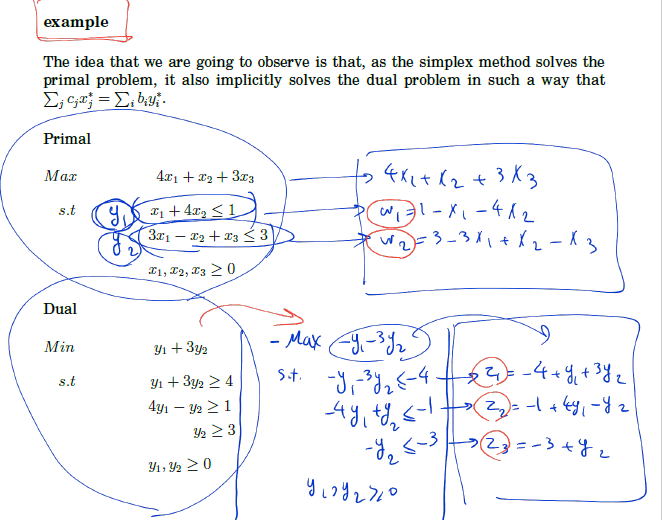
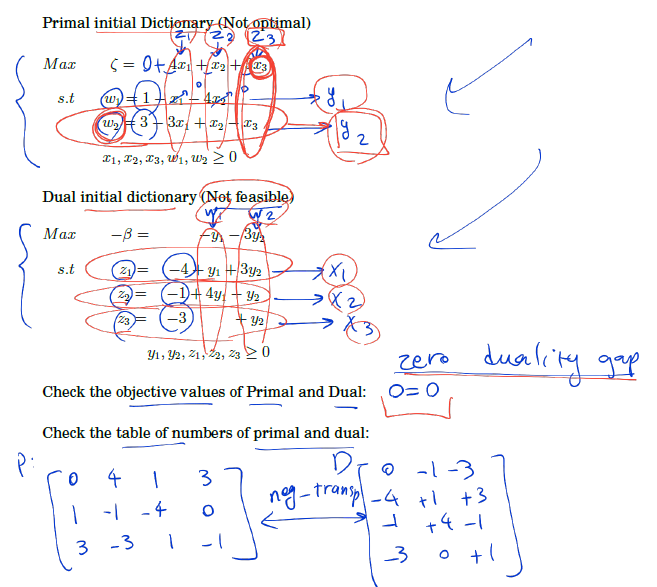

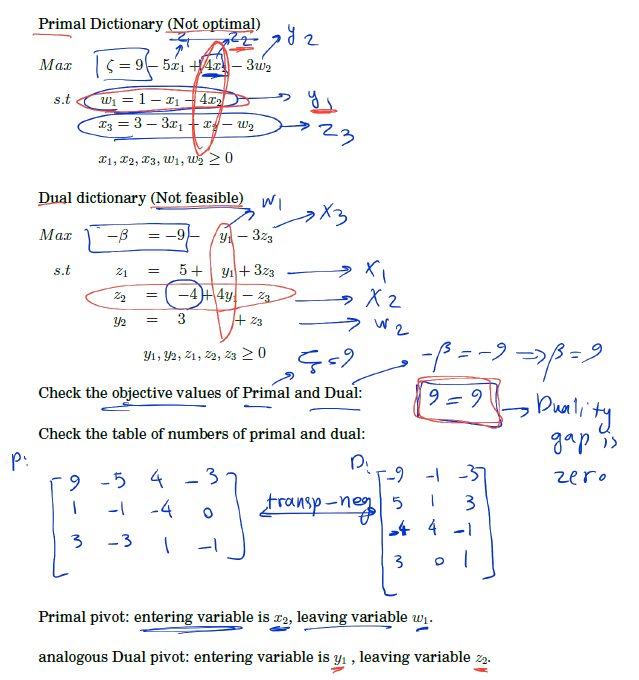

Example (Textbook)

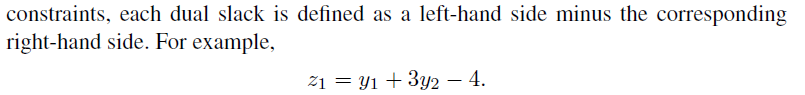

negatigve transpose



entering variable로 x1이 아닌 x3를 골라도 문제가 안되는가? 안된다. 어짜피 increase 한다.
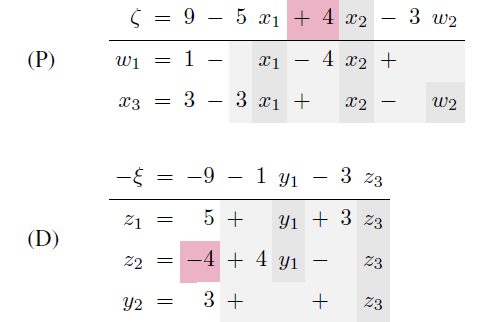


Different possibilities:







