[알고리즘] 과반수 엘리멘트

분할 정복 수도 코드

function F(x):
    if F(x)가 간단 then:
        return F(x)를 계산한 값 
               --------------
                정복 1
    
    else:
        x 를 x1, x2로 분할
        F(x1)과 F(x2)를 호출
        return F(x1), F(x2)로 F(x)를 구한 값 
        -----  -------------
        조합 2     분할 3

• 분할: 문제를 동일한 유형의 여러 하위 문제로 나눈다.
• 정복: 가장 작은 단위의 하위 문제를 해결하여 정복한다.
• 조합: 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합한다.

과반수 엘리멘트

내 풀이

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        return Counter(nums).most_common(1)[0][0]

책 풀이 1

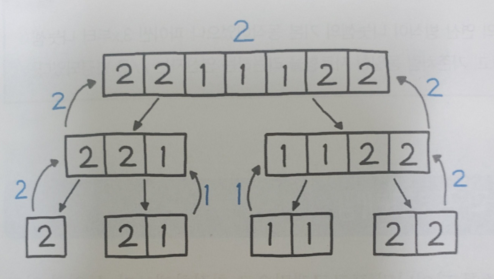
쪼갠 다음 과반수 후보군에 해당하는 엘리먼트만 리턴하면서 위로 올려준다.

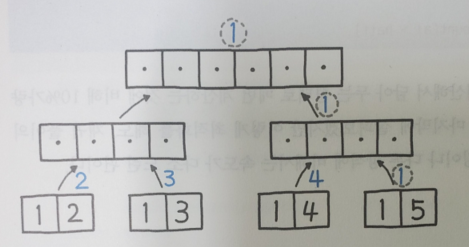
지금은 정답이 2가 루트까지 잘 올라왔지만, 만약 [1,2,1,3,1,4,1,1] 같은 입력값은 공교롭게도 2,3,4만 리턴되어서 정답을 찾을 수 없는 경우가 존재하지 않을까? 그렇지 않다. 이 문제는 과반수를 차지하는 엘리먼트를 찾는 문제이므로, 이 경우 비둘기집 원리에 따라 반드시 [1,1]이 함께 위치하는 분할이 존재한다. 따라서 1은 최소 한번 이상 반드시 리턴될 것이고, 계속 상위 분할에서 과반수를 넘어갈 것이므로 끝까지 살아남을 것이다.

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        if not nums:
            return None
        if len(nums) == 1:
            return nums[0]

        half = len(nums) // 2
        a = self.majorityElement(nums[:half])
        b = self.majorityElement(nums[half:])

        return [b,a][nums.count(a) > half] # a가 만약 현재 분할된 리스트 nums에서 과반수를 차지한다면 해당 인덱스는 1이 될 것이고,
                                            # [b,a][1]이 되어 a를 리턴할 것이다. 즉 과반수인 엘리먼트를 리턴한다. 이외에는 b를 리턴한다.                                   

책 풀이 2

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        return sorted(nums)[len(nums) // 2]

정렬하여 가운데를 지정하면 반드시 과반수 이상인 엘리먼트 일 것이다.