내 풀이
import sys
N, M = list(map(int, input().split()))
nums = list(map(int, sys.stdin.readline().split()))
acc_num = [0] * (len(nums) + 1)
for i in range(1, len(nums) + 1):
acc_num[i] = acc_num[i-1] + nums[i -1]
for m in range(M):
start_idx, end_idx = list(map(int, sys.stdin.readline().split()))
print(acc_num[end_idx] - acc_num[start_idx - 1])개념
구간합 관련 알고리즘에 대해 이야기 해보자.
구간합을 구하는 것은 원래 O(N)의 시간으로 해결할 수 밖에 없다.
효율성문제들에서 구간합 문제는 종종 등장한다. 그리고 O(N)으로 구간합을 구하려 한다면 효율성문제들을 통과할 수 없다. 적어도 O(logN)으로 구간합을 구해야 효율성 문제를 통과할 수 있다.
앞으로 알려줄 간단한 방법을 모른다면, 세그먼트 트리와 같은 조금 까다로운 방법으로 구간합을 O(logN)으로 구해야 할 것이나, 지금 알려주는 방법을 통한다면 매우 쉽게 O(1)으로 구간합을 구할 수 있다.
그 방법은 "누적합"을 구해놓는 것이다
다음과 같은 코드로 행렬의 누적합을 구해놓는다고 생각해 보자
// 누적합을 구하는 코드
for(int i = 1; i<nums.length; i++){
nums[i] += nums[i-1];
}아래와 같은 과정으로 손쉽게 누적합 배열을 완성할 수 있다
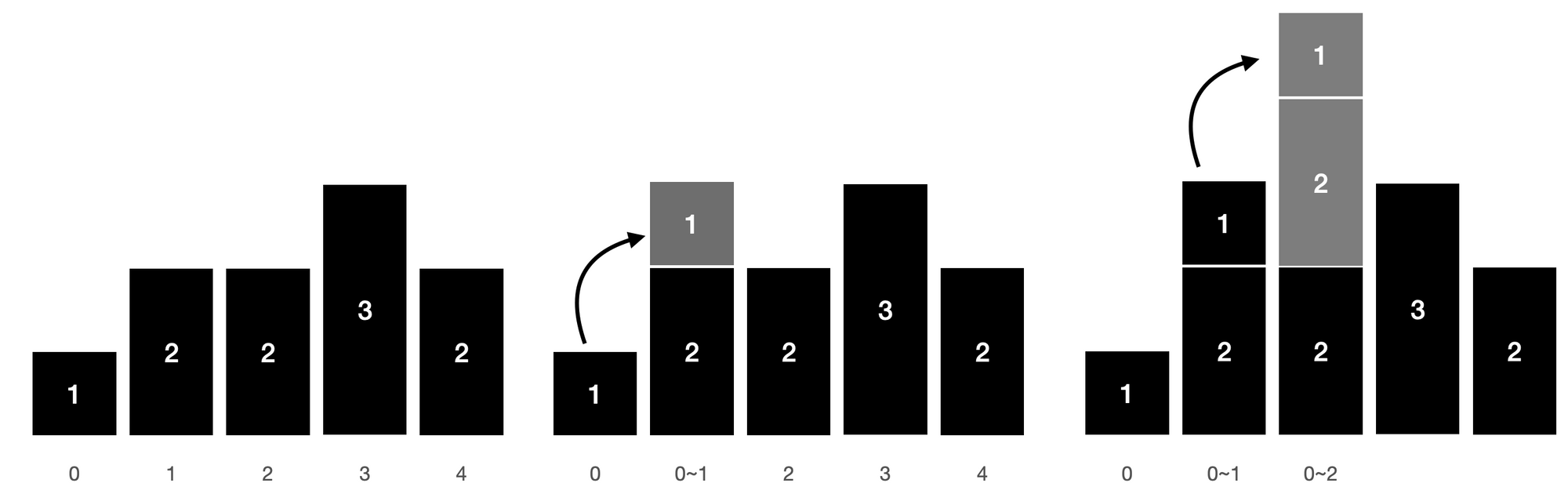
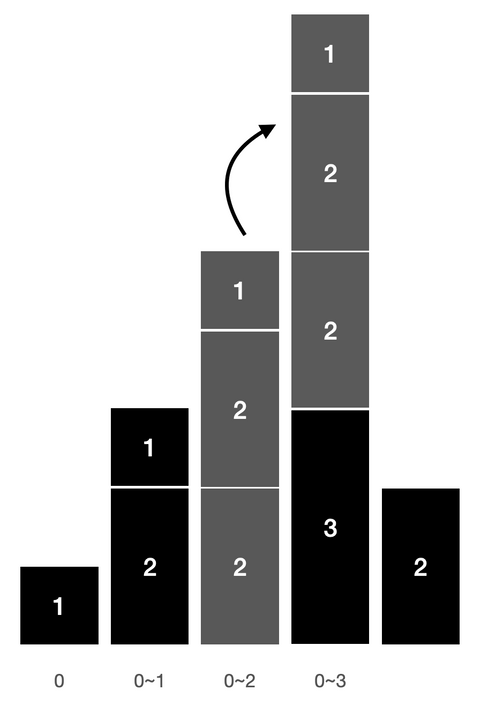
누적합을 구했다면, 이제 구간합을 O(1)에 구할 수 있다.
3~10의 구간합을 구한다고 생각해 보면, 그것은 누적합 10에서 누적합 2를 빼면 구해지는 값이다.
nums[10] - nums[2] // 기존의 3 ~ 10의 합을 구한 것이다그러나, 이 방법은 데이터가 중간중간 바뀐다면 사용할 수 없는 방법이다. 왜냐하면 데이터가 바뀔때마다 구해놓은 누적합 행렬이 선형적으로 바뀌어야 하기 때문이다.
