해시 테이블 또는 해시 맵은 키를 값에 매핑할 수 있는 구조인, 연관 배열 추상 자료형(ADT)을 구현하는 자료구조이다
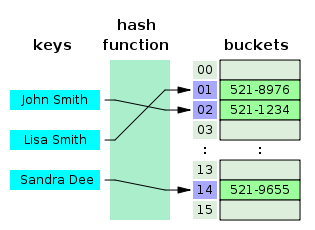
해시 함수란 임의 크기 데이터를 고정 크기 값으로 매핑하는데 사용할 수 있는 함수를 말한다.
로드 팩터(Load factor)란 해시 테이블에 저장된 데이터 개수 n을 버킷의 개수 k로 나눈 것이다.
- 로트 팩터 비율에 따라서 해시 함수를 재작성해야 될지 또는 해시 테이블의 크기를 조정해야 할지를 결정한다. 또한 이 값은 해시 함수가 키들을 잘 분산해 주는지를 말하는 효율성 측정에도 사용된다.
다양한 해싱 알고리즘이 있지만 가장 간단한 것은 모듈로 연산을 이용한 나눗셈 방식이다.h(x) = x mod m
m은 해시테이블의 크기로 일반적으로 2의 멱수에 가깝지 않은 소수를 택하는 것이 좋다.
충돌
아무리 좋은 해시 함수라도 충돌은 발생하게 된다.
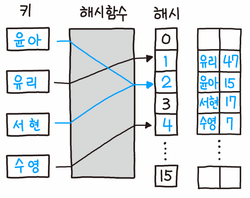
개별 체이닝 (Separate Chaining)
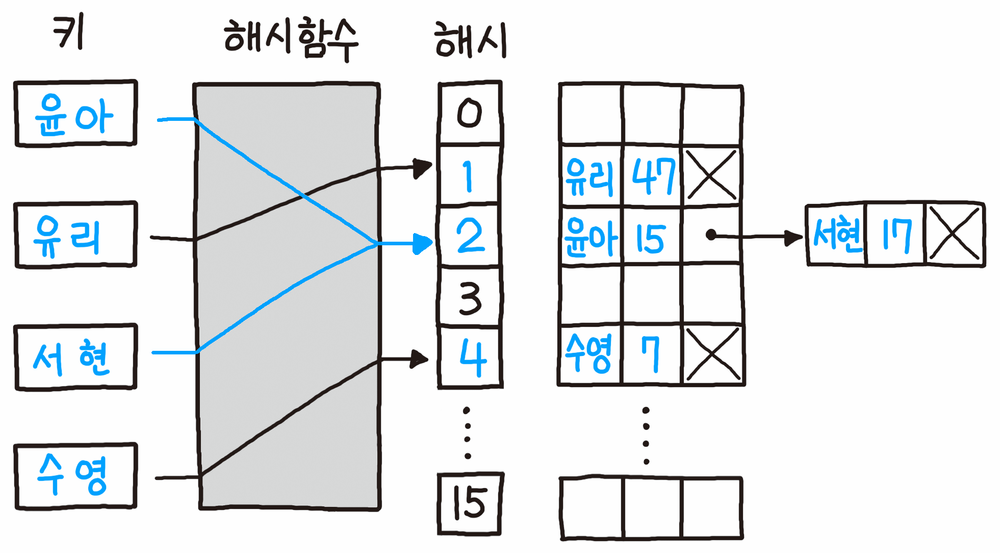
해시 테이블의 기본 방식이기도 한 개별 체이닝은 충돌 발생 시 이 그림과 같이 연결리스트로 연결하는 방식이다.
- 키의 해시 값을 계산한다
- 해시 값을 이용해 배열의 인덱스를 구한다
- 같은 인덱스가 있다면 연결 리스트로 연결한다.
잘 구현한 경우 대부분의 탐색은 O(1)이지만 최악의 경우, 즉 모든 해시 충돌이 발생했다고 가정할 경우에는 O(n)이 된다.
오픈 어드레싱 (Oepn Addressing)
오픈 어드레싱 방식은 충돌 발생 시 탐사를 통해 빈 공간을 찾아나서는 방식이다. 사실상 무한정 저장할 수 있는 체이닝 방식과 달리, 오픈 어드레싱 방식은 전체 슬롯의 개수 이상은 저장할 수 없다. 충돌이 일어나면 테이블 공간 내에서 탐사를 통해 빈 공간을 찾아 해결하며, 이 때문에 모든 원소가 반드시 자신의 해시값과 일치하는 주소에 저장된다는 보장은 없다.
선형 탐사의 한 가지 문제점은 해시 테이블에 저장되는 데이터들이 고르게 분포되지 않고 뭉치는 경향이 있다는 점이다. 해시 테이블 여기저기에 연속된 데이터 그룹들이 생기는 현상을 클러스터링이라 한다.
오픈 어드레싱 방식은 버킷 사이즈보다 큰 경우에는 삽입할 수 없다. 따라서 일정 이상 채워지면, 즉 기준이 되는 로드 팩터 비율을 넘어서게 되면, 그로스 팩터의 비율에 따라 더 큰 크기의 또 다른 버킷을 생성한 후 여기에 새롭게 복사하는 리해싱 작업이 일어난다.
파이썬의 딕셔너리는 해시 테이블로 구현되어 있으며, 오픈 어드레싱 방식으로 구현되어 있다. 오픈 어드레싱의 한 방식인 선형 탐사 방식은 일반적으로 체이닝에 비해 성능이 더 좋다. 그러나 슬롯의 80% 이상이 차게 되면, 급격한 성능 저하가 일어나며, 체이닝과 달리 전체 슬롯의 전체 개수 이상, 즉 로드 팩터 1 이상은 저장할 수 없다. 따라서 최근의 루비나 파이썬 같은 모던 언어들은 오픈 어드레싱 방식을 택해 성능을 높이는 대신, 로드 팩터를 작게 잡아 성능 저하 문제를 해결한다.
해시맵 디자인
class ListNode:
def __init__(self, key = None, value = None):
self.key = key
self.value = value
self.next = None
class MyHashMap:
def __init__(self):
self.size = 1000
self.table = collections.defaultdict(ListNode)
def put(self, key: int, value: int) -> None:
index = key % self.size
# 인덱스에 노드가 없다면 삽입 후 종료
if self.table[index].value is None:
self.table[index] = ListNode(key, value)
return
# 인덱스에 노드가 존재하는 경우 연결리스트 처리
p = self.table[index]
while p:
# 이미 존재하는 경우 업데이트하고 빠져나간다
if p.key == key:
p.value = value
return
if p.next is None:
break
p = p.next
p.next = ListNode(key, value)
def get(self, key: int) -> int:
index = key % self.size
if self.table[index].value is None:
return -1
# 노드가 존재할 때까지 일치하는 키 탐색
p = self.table[index]
while p:
if p.key == key:
return p.value
p = p.next
return -1
def remove(self, key: int) -> None:
index = key % self.size
if self.table[index].value is None:
return
# 인덱스의 첫 번째 노드일 때 삭제 처리
p = self.table[index]
if p.key == key:
self.table[index] = ListNode() if p.next is None else p.next
return
# 연결 리스트 노드 삭제
prev = p
while p:
if p.key == key:
prev.next = p.next
return
prev, p = p, p.next