👀 'Do it! 알고리즘 코딩테스트 with Python(김종관 저)'을 공부하고 정리한 내용입니다.
1. 개념
다익스트라 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘입니다.
특징으로는 에지는 모두 양수로 나타나는 것이 있습니다.
2. 원리 이해하기
2-1. 인접리스트로 그래프 구현하기
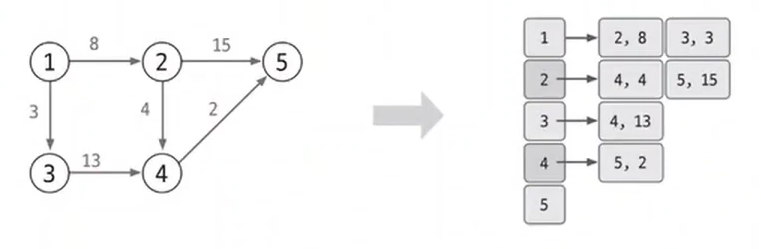
다익스트라 알고리즘을 위해서는, 가장 먼저 주어진 그래프를 인접 리스트로 구현합니다.
인접 행렬로 구해도 좋지만, 시간 복잡도 측면을 고려한다면, 인접 리스트로 구현하는 것이 좋습니다.
아래 이미지를 참고하여, 노드와 가중치가 각각 어떻게 구현되었는지 확인해봅시다.
2-2. 최단 거리 배열 초기화하기
최단 거리 배열을 만들고, 출발 노드는 0, 이외의 노드는 무한(∞)으로 초기화 합니다.
이때 실제로 구현한다고 하면, 무한이 어디 있습니까. 무한은 그냥 적당히 큰 값을 사용하면 됩니다.
실제로 구현시 99,999,999정도면 어떨까요.

2-3. 값이 가장 작은 노드 고르기
최단 거리 배열에서 현재 값이 가장 작은 노드를 고릅니다.
시작시에는 당연하게도 출발 노드가 가장 작은 노드입니다.
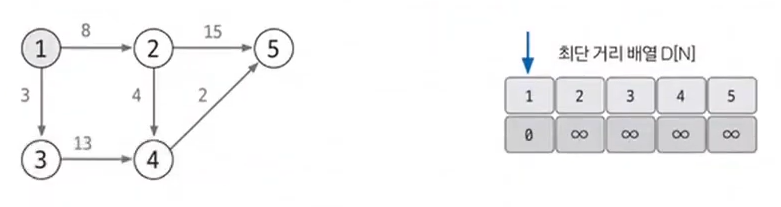
2-4. 최단 거리 배열 업데이트하기
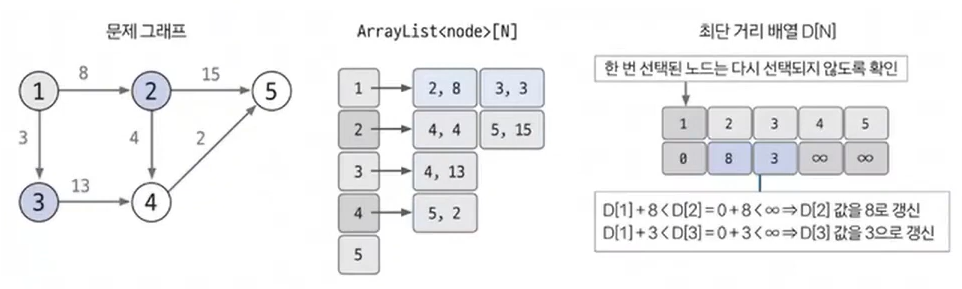
선택된 노드에 연결된 에지의 값을 바탕으로 다른 노드의 값을 업데이트 합니다. 2-1에서 저장해 놓은 연결 리스트를 이용해 현재 선택된 노드의 에지들을 탐색하고 업데이트 하면 됩니다. 연결 노드의 최단 거리는 다음과 같이 두 값 중 더 작은 값으로 업데이트합니다.
업데이트 방법
- Min(선택 노드의 최단 거리 배열의 값 + 에지 가중치, 연결 노드의 최단 거리 배열의 값)
2-5. 과정 3~4를 반복해 최단 거리 배열 완성하기
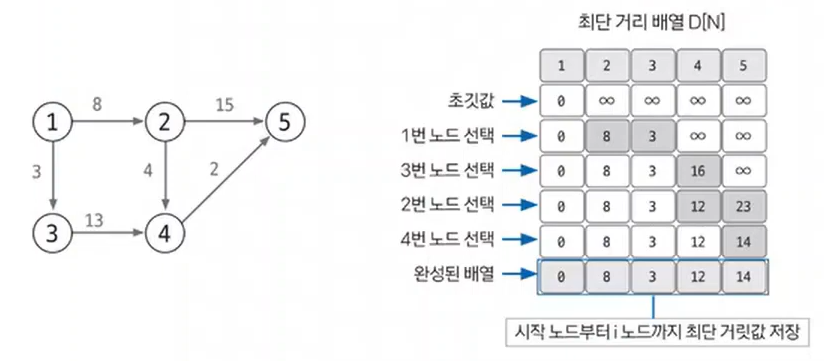
모든 노드가 처리될 때까지 과정 3~4를 반복합니다. 과정 4에서 선택 노드가 될 때마다 다시 선택되지 않도록 방문 배열을 만들어 처리하고 모든 노드가 선택될 때까지 반복하면 최단거리 배열이 완성됩니다.
BOJ 1753 최단 경로 구하기
문제
방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오. 단, 모든 간선의 가중치는 10 이하의 자연수이다.
입력
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가 주어진다. 셋째 줄부터 E개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수 (u, v, w)가 순서대로 주어진다. 이는 u에서 v로 가는 가중치 w인 간선이 존재한다는 뜻이다. u와 v는 서로 다르며 w는 10 이하의 자연수이다. 서로 다른 두 정점 사이에 여러 개의 간선이 존재할 수도 있음에 유의한다.
출력
첫째 줄부터 V개의 줄에 걸쳐, i번째 줄에 i번 정점으로의 최단 경로의 경로값을 출력한다. 시작점 자신은 0으로 출력하고, 경로가 존재하지 않는 경우에는 INF를 출력하면 된다.
입출력 예
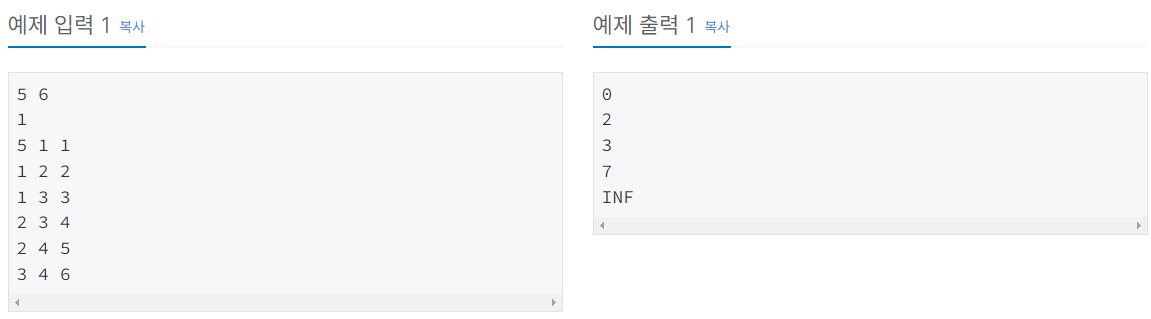
강의 내 풀이
import sys
from queue import PriorityQueue
V, E = map(int, sys.stdin.readline().split()) # 노드개수, 에지개
K = int(input()) # 시작 노드
distance = [sys.maxsize]*(V+1)
visited = [False] * (V+1)
myList = [[] for _ in range(V+1)]
q = PriorityQueue()
for _ in range(E):
u, v, w = map(int, sys.stdin.readline().split())
myList[u].append((v, w))
q.put((0,K))
distance[K] = 0
while q.qsize() > 0:
current = q.get()
c_v = current[1]
if visited[c_v]:
continue
visited[c_v] = True
for tmp in myList[c_v]:
next = tmp[0]
value = tmp[1]
if distance[next] > distance[c_v] + value:
distance[next] = distance[c_v] + value
q.put((distance[next], next))
for i in range(1, V+1):
if distance[i] != sys.maxsize:
print(distance[i])
else:
print('INF')지피티는 이렇게 풀더라
import heapq
import sys
# 다익스트라 알고리즘을 사용하여 최단 경로를 찾는 함수
def dijkstra(graph, start):
distances = {node: float('inf') for node in graph} # 시작 정점으로부터의 거리를 저장하는 딕셔너리
distances[start] = 0 # 시작 정점의 거리는 0
queue = [(0, start)] # 우선순위 큐를 사용하여 방문할 정점과 거리를 저장하는 리스트
while queue:
current_distance, current_node = heapq.heappop(queue) # 가장 가까운 정점과 그 거리를 가져옴
if current_distance > distances[current_node]:
continue # 이미 처리된 정점이라면 스킵
for neighbor, weight in graph[current_node].items():
distance = current_distance + weight
if distance < distances[neighbor]: # 현재 경로가 더 짧다면 갱신
distances[neighbor] = distance
heapq.heappush(queue, (distance, neighbor)) # 다음 정점을 위해 큐에 추가
return distances
# 정점 개수(V), 간선 개수(E) 입력
V, E = map(int, input().split())
start = int(input()) # 시작 정점 번호 입력
graph = {i: {} for i in range(1, V + 1)} # 각 정점마다 인접한 정점과 가중치를 저장하는 그래프
# 간선 정보 입력 및 그래프 구성
for _ in range(E):
u, v, w = map(int, input().split()) # u에서 v로 가는 가중치 w의 간선
if v in graph[u]:
graph[u][v] = min(graph[u][v], w) # 이미 저장된 간선이 있다면 더 작은 가중치로 업데이트
else:
graph[u][v] = w # 처음 보는 간선이라면 가중치 저장
# 다익스트라 알고리즘을 통해 최단 경로 계산
distances = dijkstra(graph, start)
# 결과 출력
for i in range(1, V + 1):
if distances[i] == float('inf'):
print("INF") # 시작 정점으로부터 도달할 수 없는 경우
else:
print(distances[i]) # 최단 거리 출력
