그래프에서 최단거리를 구하는 알고리즘은 여러개가 있습니다.
BFS, 다익스트라, 벨만-포드, 플로이드-워셜... 그 중에서 오늘은 플로이드-워셜에 대해 알아봅시다.

👀 'Do it! 알고리즘 코딩테스트 with Python(김종관 저)'을 공부하고 정리한 내용입니다.

1. 개념

플로이드 워셜은 모든 노드간에 최단 경로를 탐색합니다. 음수 가중치 에지가 있어도 수행이 가능합니다. 또한, 동적 계획법의 원리를 이용하여 알고리즘에 접근한다는 특징이 있습니다.

2. 원리 이해하기

플로이드 워셜 알고리즘을 도출하는 가장 핵심적인 원리는 A 노드에서 B 노드까지 최단 경로를 구했다고 가정했을 때 최단 경로 위에 K 노드가 존재한다면 그것을 이루는 부분 경로 역시 최단경로라는 겁니다.

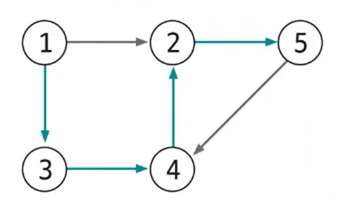
색칠된 에지 경로가 1 → 5 최단 경로라면 1 → 4 최단 경로와 4 → 5 최단경로 역시 색칠된 에지로 이뤄질 수 밖에 없습니다. 즉, 전체 경로의 최단 경로는 부분 경로의 최단 경로의 조합으로 이워진다는 의미가 됩니다. 이 원리로 다음과 같은 점화식을 도출할 수 있습니다.

도출한 플로이드 워셜 점화식
D[S][E] = Math.min(D[S][E], D[S][K] + D[K][E])

2-1. 리스트를 선언하고 초기화하기

D[S][E]는 노드 S에서 노드 E까지의 최단 거리를 저장하는 리스트라 정의합니다. S와 E의 값이 같은 같은 0, 다른 칸은 ∞로 초기화합니다. 여기에서 S == E는 자기 자신에게 가는 데 걸리는 최단 경로 값을 의미하기 때문입니다.

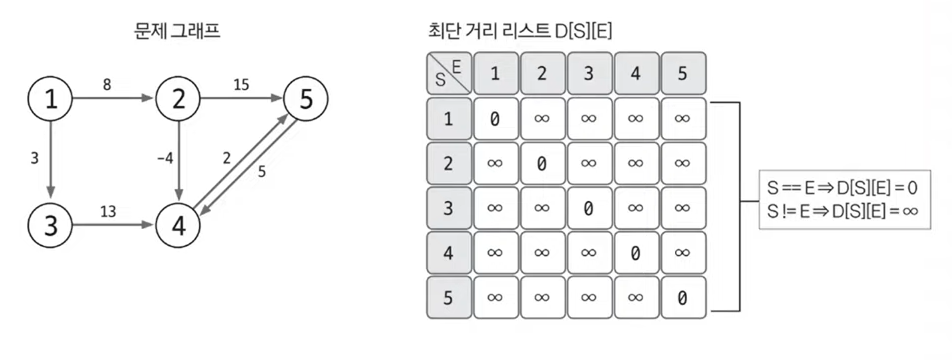
2-2. 최단 거리 리스트에 그래프 데이터 저장하기

출발 노드는 S, 도착 노드는 E, 이 에지의 가중치가 W라고 했을 때 D[S][E] = W로 에지의 정보를 리스트에 입력합니다. 이로써 플로이드-워셜 알고리즘은 그래프를 인접 행렬로 표현한다는 것을 알 수 있습니다.

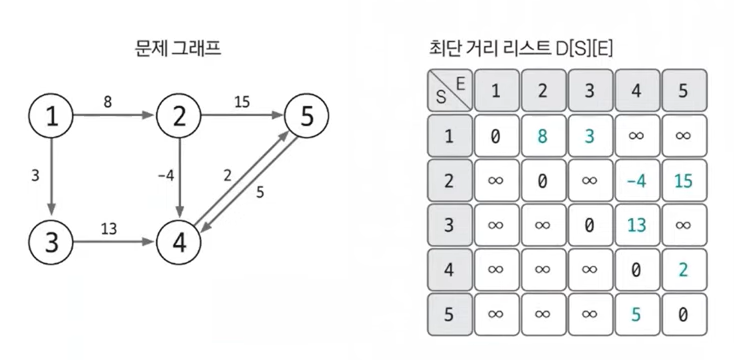
2-3. 점화식으로 리스트 업데이트하기

기존에 구했던 점화식을 3중 for 문의 형태로 반복하면서 리스트의 값을 업데이트 합니다.

# 플로이드 워셜 알고리즘 로직
for 경유 K에 관해 (1 ~ N)    # N: 노드 개수
	for 출발 노드 S에 관해 (1 ~ N)
    	for 도착 노드 E에 관해 (1 ~ N)
        	D[S][E] = Math.min(D[S][E], D[S][K] + D[K][E])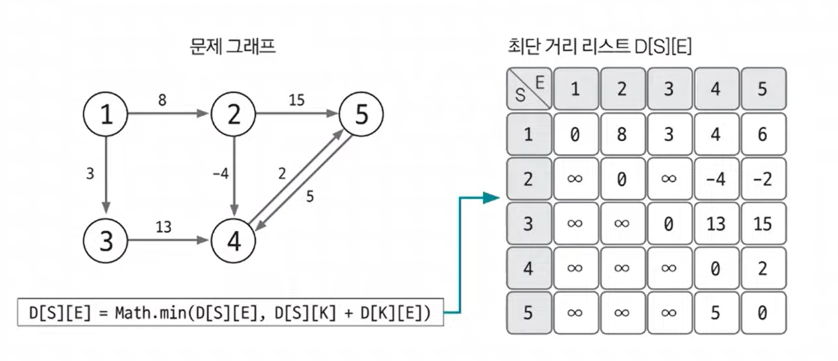

완성된 리스트는 모든 노드 간의 최단 거리를 알려줍니다. 예를 들어 1번 노드에서 5번 노드까지 가는 최단 거리는 D[1][5] = 6으로 나타난다는 것을 알 수 있습니다.

플로이드-워셜 알고리즘은 모든 노드 간의 최단 거리를 확인해주기 때문에 시간 복잡도가 O(V**3)으로 빠르지 않은 편입니다. 이에 따라 플로이드-워셜 알고리즘을 사용해야하는 문제가 나오면 일반적으로 노드 개수의 범위가 다른 그래프에 비해 적게 나타난다는 것을 알 수 있습니다.

BOJ 11404 플로이드

문제

n(2 ≤ n ≤ 100)개의 도시가 있다. 그리고 한 도시에서 출발하여 다른 도시에 도착하는 m(1 ≤ m ≤ 100,000)개의 버스가 있다. 각 버스는 한 번 사용할 때 필요한 비용이 있다.

모든 도시의 쌍 (A, B)에 대해서 도시 A에서 B로 가는데 필요한 비용의 최솟값을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가 주어진다. 버스의 정보는 버스의 시작 도시 a, 도착 도시 b, 한 번 타는데 필요한 비용 c로 이루어져 있다. 시작 도시와 도착 도시가 같은 경우는 없다. 비용은 100,000보다 작거나 같은 자연수이다.

시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있다.

출력

n개의 줄을 출력해야 한다. i번째 줄에 출력하는 j번째 숫자는 도시 i에서 j로 가는데 필요한 최소 비용이다. 만약, i에서 j로 갈 수 없는 경우에는 그 자리에 0을 출력한다.

입출력예

풀이

import sys

# 입력을 빠르게 받기 위해 sys.stdin.readline 사용
input = sys.stdin.readline

# 도시의 개수 N과 버스 노선의 개수 M 입력
N = int(input())
M = int(input())
distance = [[sys.maxsize for j in range(N+1)] for i in range(N+1)]

# 자기 자신으로 가는 경로의 거리는 0으로 초기화
for i in range(1, N+1):
    distance[i][i] = 0

# 버스 정보 입력받아 그래프에 거리 저장
for _ in range(M):
    s, e, w = map(int, input().split())
    if distance[s][e] > w:  # 최소 거리를 저장
        distance[s][e] = w

# 플로이드 워셜 알고리즘 수행
for k in range(1, N + 1):
    for i in range(1, N + 1):
        for j in range(1, N + 1):
            # 더 작은 거리로 갱신할 수 있다면 갱신
            if distance[i][j] > distance[i][k] + distance[k][j]:
                distance[i][j] = distance[i][k] + distance[k][j]

# 결과 출력
for i in range(1, N + 1):
    for j in range(1, N + 1):
        if distance[i][j] == sys.maxsize:
            print(0, end=' ')
        else:
            print(distance[i][j], end=' ')
    print()  # 줄 바꿈