최소 비용으로 최단 거리 구하기

이러한 알고리즘에는 다익스트라, 벨만 포드, 플로이드 워샬 등 다양한 알고리즘이 있지만 오늘은 벨만 포드 알고리즘에 대해 알아보도록 합시당

벨만-포드 알고리즘이란?

일단 벨만 포드가 누군데 ㅇㅅㅇ
해당 알고리즘을 만든 학자들의 성을 따서 만들었다고 합니다 아하 해결

다익스트라 알고리즘과 같이 그래프가 가중치를 가지는 간선으로 이루어져 있을 때 한 정점에서 나머지 다른 점까지의 최단 거리를 찾는 것이 목적이다.
해당 알고리즘의 시간 복잡도는 O(VE)로 O((V+E)lgV)인 다익스트라 알고리즘보다 느리다.

그렇다면 왜 벨만 포드 알고리즘을 사용하는 것일까?
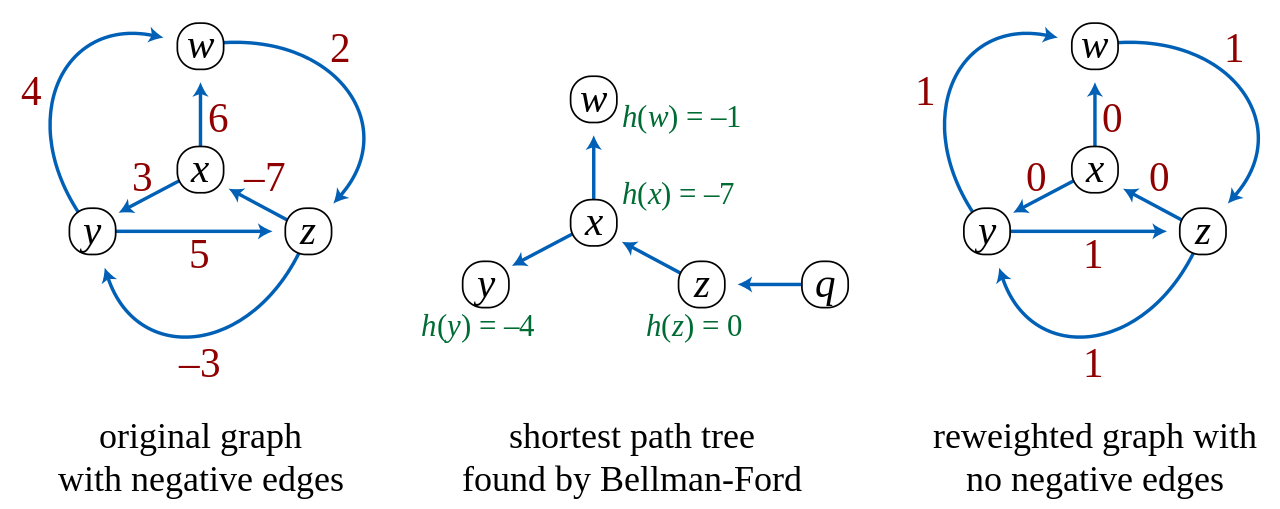
왜냐하면 벨만 포드 알고리즘은 가중치가 음수라도 쓸 수 있기 때문이다.
그러나 음수 사이클이 그래프에 있으면 정확한 값을 구할 수 없을 것이다. 계속 무한으로 -를 해주면 최소 값이 계속해서 줄어들면서 끝나지 않을 테니까...

이 개념을 가지고 풀어봐야할 문제가 있다

💡 문제 1
V개의 마을와 E개의 도로로 구성되어 있는 도시가 있다. 도로는 마을과 마을 사이에 놓여 있으며, 일방 통행 도로이다. 마을에는 편의상 1번부터 V번까지 번호가 매겨져 있다고 하자.
당신은 도로를 따라 운동을 하기 위한 경로를 찾으려고 한다. 운동을 한 후에는 다시 시작점으로 돌아오는 것이 좋기 때문에, 우리는 사이클을 찾기를 원한다. 단, 당신은 운동을 매우 귀찮아하므로, 사이클을 이루는 도로의 길이의 합이 최소가 되도록 찾으려고 한다.
도로의 정보가 주어졌을 때, 도로의 길이의 합이 가장 작은 사이클을 찾는 프로그램을 작성하시오. 두 마을을 왕복하는 경우도 사이클에 포함됨에 주의한다.

💡 입력
첫째 줄에 V와 E가 빈칸을 사이에 두고 주어진다. (2 ≤ V ≤ 400, 0 ≤ E ≤ V(V-1)) 다음 E개의 줄에는 각각 세 개의 정수 a, b, c가 주어진다. a번 마을에서 b번 마을로 가는 거리가 c인 도로가 있다는 의미이다. (a → b임에 주의) 거리는 10,000 이하의 자연수이다. (a, b) 쌍이 같은 도로가 여러 번 주어지지 않는다.

💡 출력
첫째 줄에 최소 사이클의 도로 길이의 합을 출력한다. 운동 경로를 찾는 것이 불가능한 경우에는 -1을 출력한다.

#include <iostream>
#include <vector>
#include <limits> // for numeric_limits
using namespace std;

int dist[401]; // 각 노드의 거리 10000 이하임
struct Edge
{
    int s, e, val; // 시작노드, 끝노드, 비용
    Edge(int a, int b, int c)
    {
        s = a;
        e = b;
        val = c;
    }
};

int main()
{
    vector<Edge> Ed; // 노드와 노드 사이 간선들의 배열
    int n, m, a, b, c, s, e;
    cin >> n >> m; // n : 노드의 수 m : 간선의 수 

    for (int i = 1; i <= m; i++)
    {
        cin >> a >> b >> c; // 간선과 간선, 그 비용 입력
        Ed.push_back(Edge(a, b, c));
    }

    for (int i = 1; i <= n; i++)
    {
        dist[i] = numeric_limits<int>::max(); // 모든 초기 비용(거리)을 아주 큰 값으로 초기화
    }

    cin >> s >> e;
    dist[s] = 0; // 시작 노드는 비용(거리)가 0

    for (int i = 0; i < n - 1; i++) // 순회는 n-1만큼 돌아야함
    {
        for (int j = 0; j < Ed.size(); j++) // push_back된 Ed만큼 
        {
            int u = Ed[j].s;
            int v = Ed[j].e;
            int w = Ed[j].val;

            if (dist[u] != numeric_limits<int>::max() && dist[u] + w < dist[v])
            {
                dist[v] = dist[u] + w;
            }
        }
    }

    // 음의 싸이클 체크
    for (int j = 0; j < Ed.size(); j++) {
        int u = Ed[j].s;
        int v = Ed[j].e;
        int w = Ed[j].val;
        if (dist[u] != numeric_limits<int>::max() && dist[u] + w < dist[v]) { // 음의 싸이클
            cout << "-1" << endl;
            return 0;
        }
    }

    cout << dist[e] << endl;
    return 0;
}

이렇게 풀었는데요 하나씩 알아봅시다.

int dist[401]; // 각 노드의 거리 10000 이하임
struct Edge
{
	int s, e, val; // 시작노드, 끝노드, 비용
	Edge(int a, int b, int c)
	{
		// 사용자가 인자들을 입력해줄 예정
		s = a;
		e = b;
		val = c;
	}
};

우선 정점의 수가 2 ≤ V ≤ 400이므로 배열을 넉넉히 401로 잡아주고
각 간선이 공통으로 가질 정보들을 담는 구조체를 만들었다.

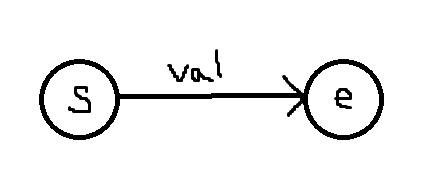
  vector<Edge> Ed; // 노드와 노드 사이 간선들의 배열
  int n, m, a, b, c, s, e;
  cin >> n >> m; // n : 노드의 수 m : 간선의 수 

간선의 배열을 vector 컨테이너에 담고,
노드와 간선의 수를 cin으로 입력받는다.

 for (int i = 1; i <= m; i++)
    {
        cin >> a >> b >> c; // 간선과 간선, 그 비용 입력
        Ed.push_back(Edge(a, b, c));
    }

for문으로 간선의 수만큼 간선 정보들을 입력해줄 것이다.
그리고 아까만든 벡터 배열에 하나씩 push_back해준다.

  for (int i = 1; i <= n; i++)
    {
        dist[i] = numeric_limits<int>::max();
        // 모든 초기 비용(거리)을 아주 큰 값으로 초기화
    }
 	cin >> s >> e;
    dist[s] = 0; // 시작 노드는 비용(거리)가 0

각 노드의 비용을 대충 큰 값으로 초기화 해놓고 변경해준다.

for (int i = 0; i < n - 1; i++) // 순회는 n-1만큼 돌아야함
    {
        for (int j = 0; j < Ed.size(); j++) // push_back된 Ed만큼 
        {
            int u = Ed[j].s;
            int v = Ed[j].e;
            int w = Ed[j].val;

            if (dist[u]
            != numeric_limits<int>::max()
            && dist[u] + w // 시작노드 비용 + 노드 간 비용
            < dist[v]) // 끝 노드 비용
            {
                dist[v] = dist[u] + w;
                // 끝 노드 비용에 시작노드 + 노드 간 비용을 대입
            }
        }
    }

노드 간 비용을 확인해 끝 노드 값을 구해주고

 // 음의 싸이클 체크
    for (int j = 0; j < Ed.size(); j++) {
        int u = Ed[j].s;
        int v = Ed[j].e;
        int w = Ed[j].val;
        if (dist[u]
        != numeric_limits<int>::max()
        && dist[u] + w
        < dist[v])
        { // 음의 싸이클
            cout << "-1" << endl;
            return 0;
        }

음의 사이클이 나오면 -1을 출력해준다. -> 운동 경로를 찾을 수 없음

    cout << dist[e] << endl;
    return 0;

이로써 최소 사이클 길이를 알 수 있게 되었다. 야호!

추가적으로 이를 그림으로 알아보고자 하면,

-> 다시 풀어보기
https://www.acmicpc.net/problem/11657