큐(Queues)

---

• 자료(data element)를 보관할 수 있는 (선형)구조

• 단, 넣을 때에는 한 쪽 끝에서 밀어 넣어야 함

  → 인큐(enqueue) 연산

• 꺼낼 때에는 반대 쪽에서 뽑아 꺼내야 함

  → 디큐(dequeue) 연산

• 선입선출(FIFO, First-In-First-Out)

• 선형 자료구조

큐의 동작

---

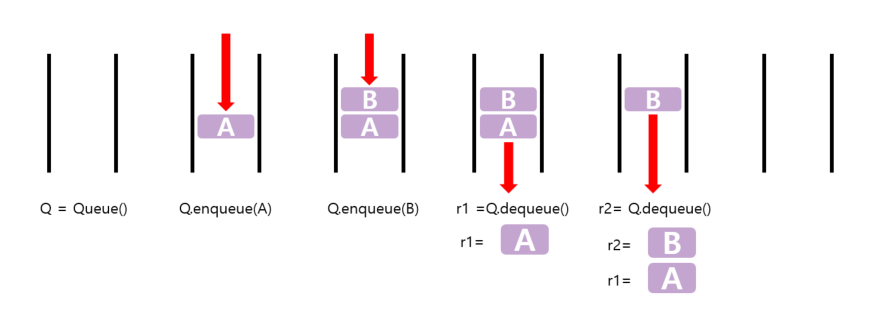
큐의 추상적 자료구조 구현

---

1. 배열(Array)를 이용하여 구현

• python 리스트의 메소드들을 이용

2. 연결 리스트(Linked List)를 이용하여 구현

• 이전에 구현한 양방향 연결 리스트 이용

연산의 정의

---

• size() : 현재 큐에 들어있는 데이터 원소의 수를 구함
• isEmpty() : 현재 큐가 비어 있는지를 판단
• enqueue(x) : 데이터 원소 x를 큐에 추가
• dequeue() : 큐의 맨 앞에 저장된 데이터 원소를 제거(또는 반환)
• peek() : 큐의 맨 앞에 저장된 데이터 원소를 반환(제거하지 않음)

배열로 구현한 큐

---

# 배열로 구현한 큐
class ArrayQueue:
    # 빈 큐를 초기화
    def __init__(self):
        self.data = []
        
    # 큐의 크기를 리턴
    def size(self):
        return len(self.data)

    # 큐가 비어있는지 판단
    def isEmpty(self):
        return self.size() == 0
    
    # 데이터 원소 추가 연산
    def enqueue(self, item):
        self.data.append(item)
        
    # 데이터 원소 삭제 연산
    def dequeue(self):
        return self.data.pop(0)
    
    # 큐의 맨 앞 원소 반환
    def peek(self):
        return self.data[0]

배열로 구현한 큐의 연산 복잡도

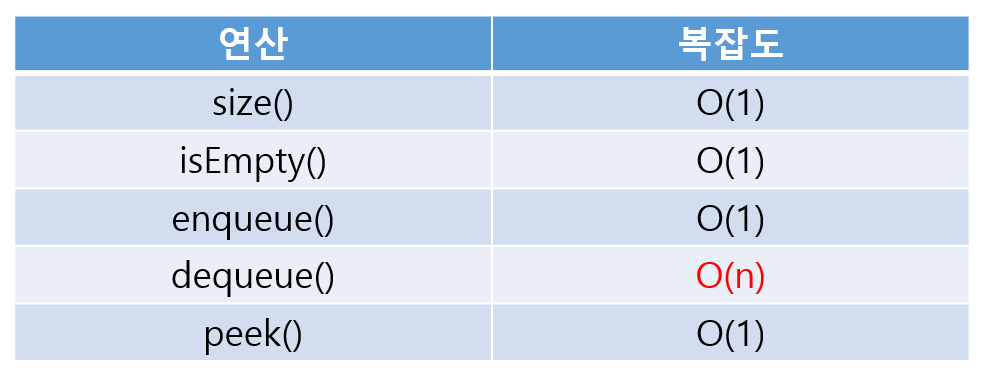
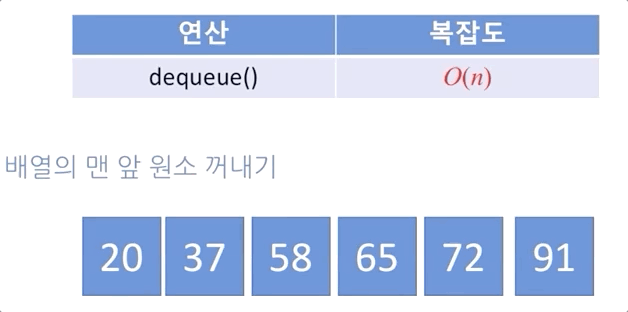
• 데이터 삭제 연산(dequeue)은 큐의 길이가 길어질수록 그 만큼 오래걸린다
• 큐의 길이에 비례하는 복잡도를 가진다
• e.g. 맨 앞의 원소가 삭제가 되면, 그 뒤에 있는 데이터들이 하나씩 앞으로 당겨서 와야함으로 큐의 길이만큼 연산이 일어남

이중 연결 리스트로 큐를 구현

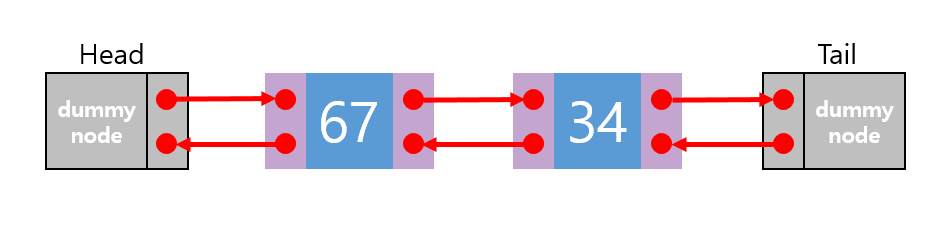
class Node:

    def __init__(self, item):
        self.data = item
        self.prev = None
        self.next = None

class DoublyLinkedList:

    def __init__(self):
        self.nodeCount = 0
        self.head = Node(None)
        self.tail = Node(None)
        self.head.prev = None
        self.head.next = self.tail
        self.tail.prev = self.head
        self.tail.next = None

    def __repr__(self):
        if self.nodeCount == 0:
            return 'LinkedList: empty'

        s = ''
        curr = self.head
        while curr.next.next:
            curr = curr.next
            s += repr(curr.data)
            if curr.next.next is not None:
                s += ' -> '
        return s

    def getLength(self):
        return self.nodeCount

    def traverse(self):
        result = []
        curr = self.head
        while curr.next.next:
            curr = curr.next
            result.append(curr.data)
        return result

    def reverse(self):
        result = []
        curr = self.tail
        while curr.prev.prev:
            curr = curr.prev
            result.append(curr.data)
        return result

    def getAt(self, pos):
        if pos < 0 or pos > self.nodeCount:
            return None

        if pos > self.nodeCount // 2:
            i = 0
            curr = self.tail
            while i < self.nodeCount - pos + 1:
                curr = curr.prev
                i += 1
        else:
            i = 0
            curr = self.head
            while i < pos:
                curr = curr.next
                i += 1

        return curr

    def insertAfter(self, prev, newNode):
        next = prev.next
        newNode.prev = prev
        newNode.next = next
        prev.next = newNode
        next.prev = newNode
        self.nodeCount += 1
        return True

    def insertAt(self, pos, newNode):
        if pos < 1 or pos > self.nodeCount + 1:
            return False

        prev = self.getAt(pos - 1)
        return self.insertAfter(prev, newNode)

    def popAfter(self, prev):
        curr = prev.next
        next = curr.next
        prev.next = next
        next.prev = prev
        self.nodeCount -= 1
        return curr.data

    def popAt(self, pos):
        if pos < 1 or pos > self.nodeCount:
            raise IndexError('Index out of range')

        prev = self.getAt(pos - 1)
        return self.popAfter(prev)

    def concat(self, L):
        self.tail.prev.next = L.head.next
        L.head.next.prev = self.tail.prev
        self.tail = L.tail

        self.nodeCount += L.nodeCount

#################################################
class LinkedListQueue:

    def __init__(self):
        self.data = DoublyLinkedList()

    def size(self):
        return self.data.nodeCount

    def isEmpty(self):
        return self.data.nodeCount==0

    def enqueue(self, item):
        node = Node(item)
        self.data.insertAt(self.size()+1,node)

    def dequeue(self):
        return self.data.popAt(1)

    def peek(self):
        return self.data.head.next.data
#################################################

def solution(x):
    return 0

참고 - 큐 라이브러리

from pythonds.basic.queue import Queue

Q = Queue()
dir(Q)

[실습] 양방향 연결 리스트로 구현하는 큐

문제

어서와! 자료구조와 알고리즘은 처음이지? 14강 실습: 양방향 연결 리스트로 구현하는 큐

문제 설명

양방향 연결 리스트를 활용하여 큐 (queue) 의 추상적 자료구조 (abstract data structure) 구현을 완성하세요.

정의하고자 하는 큐의 추상적 자료구조는 class LinkedListQueue 로 구현됩니다. 이 문제는 해당 클래스의 메서드들의 구현을 빈칸 채우기 형태로 완성하는 것으로 되어 있으며, 이 클래스의 구현은 L120 부터 시작합니다.

그 위에는 (LL1-117) 이 추상적 자료구조를 구현하기 위해서 이용할 class DoublyLinkedList 와, 또한 여기서 이용하는 class Node 의 구현이 정의되어 있습니다. 이 코드는 이전의 양방향 연결 리스트 강의에서 다루어진 것과 완전히 동일합니다.

정확성 테스트는 class LinkedListQueue 의 각 메서드가 올바르게 구현되어 있는지를 검사합니다. 코드 실행 을 눌렀을 때 예시 테스트 케이스를 통과하는 것은 아무런 의미가 없습니다.

---

나의 풀이

solution.py

class Node:

    def __init__(self, item):
        self.data = item
        self.prev = None
        self.next = None

class DoublyLinkedList:

    def __init__(self):
        self.nodeCount = 0
        self.head = Node(None)
        self.tail = Node(None)
        self.head.prev = None
        self.head.next = self.tail
        self.tail.prev = self.head
        self.tail.next = None

    def __repr__(self):
        if self.nodeCount == 0:
            return 'LinkedList: empty'

        s = ''
        curr = self.head
        while curr.next.next:
            curr = curr.next
            s += repr(curr.data)
            if curr.next.next is not None:
                s += ' -> '
        return s

    def getLength(self):
        return self.nodeCount

    def traverse(self):
        result = []
        curr = self.head
        while curr.next.next:
            curr = curr.next
            result.append(curr.data)
        return result

    def reverse(self):
        result = []
        curr = self.tail
        while curr.prev.prev:
            curr = curr.prev
            result.append(curr.data)
        return result

    def getAt(self, pos):
        if pos < 0 or pos > self.nodeCount:
            return None

        if pos > self.nodeCount // 2:
            i = 0
            curr = self.tail
            while i < self.nodeCount - pos + 1:
                curr = curr.prev
                i += 1
        else:
            i = 0
            curr = self.head
            while i < pos:
                curr = curr.next
                i += 1

        return curr

    def insertAfter(self, prev, newNode):
        next = prev.next
        newNode.prev = prev
        newNode.next = next
        prev.next = newNode
        next.prev = newNode
        self.nodeCount += 1
        return True

    def insertAt(self, pos, newNode):
        if pos < 1 or pos > self.nodeCount + 1:
            return False

        prev = self.getAt(pos - 1)
        return self.insertAfter(prev, newNode)

    def popAfter(self, prev):
        curr = prev.next
        next = curr.next
        prev.next = next
        next.prev = prev
        self.nodeCount -= 1
        return curr.data

    def popAt(self, pos):
        if pos < 1 or pos > self.nodeCount:
            raise IndexError('Index out of range')

        prev = self.getAt(pos - 1)
        return self.popAfter(prev)

    def concat(self, L):
        self.tail.prev.next = L.head.next
        L.head.next.prev = self.tail.prev
        self.tail = L.tail

        self.nodeCount += L.nodeCount

class LinkedListQueue:

    def __init__(self):
        self.data = DoublyLinkedList()

    def size(self):
        return self.data.nodeCount

    def isEmpty(self):
        return self.data.nodeCount==0

    def enqueue(self, item):
        node = Node(item)
        self.data.insertAt(self.size()+1,node)

    def dequeue(self):
        return self.data.popAt(1)

    def peek(self):
        return self.data.head.next.data

def solution(x):
    return 0