이진 트리의 추상적 자료구조

연산의 정의

• size() : 현재 트리에 포함되어 있는 노드의 수를 구함
• depth() : 현재 트리의 깊이(또는 높이;height)를 구함
• 순회(traversal)

노드(Node)

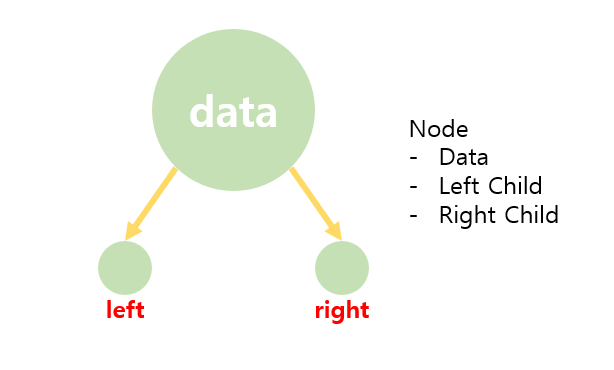
# 이진트리의 구현 - 노드(node)
class Node:
    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None

트리 클래스

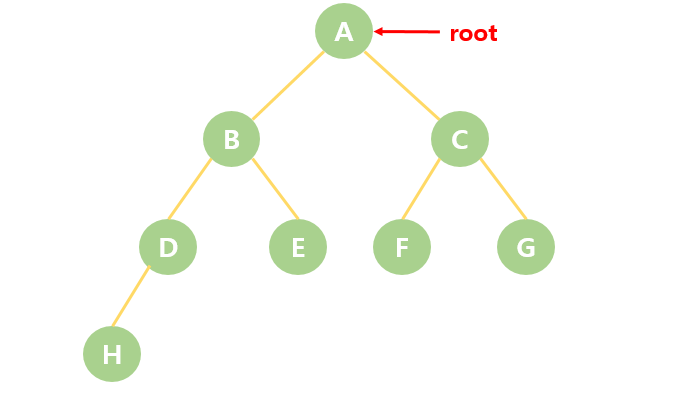
# 이진 트리의 구현 - 트리(tree)
class BinaryTree:
    def __init__(self, r):
        self.root = r

size()

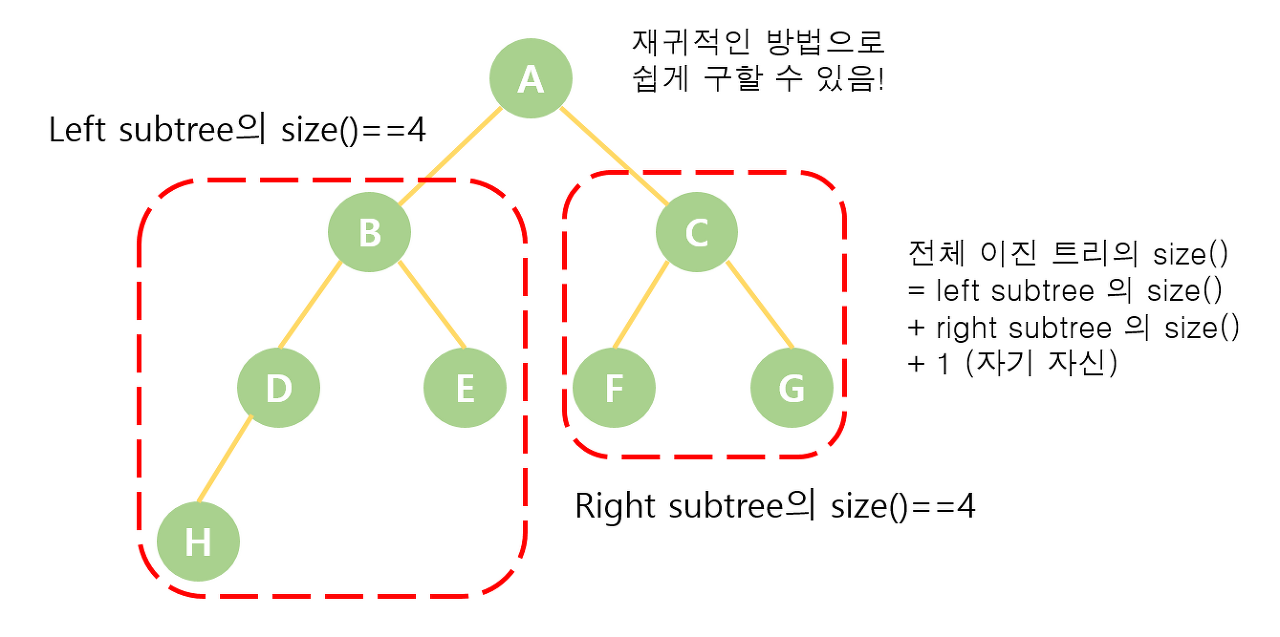
class Node:

	# 이진 트리의 크기 - 재귀함수 이용
    def size(self):
        l = self.left.size() if self.left else 0 # 왼쪽 서브트리
        r = self.right.size() if self.right else 0 # 오른쪽 서브트리
        return l + r + 1 # 왼쪽 + 오른쪽 + 자기자신(+1)
 

class BinaryTree:
	
    # 크기 구하기
    def size(self):
        if self.root:
            return self.root.size()
        else:
            return 0

depth()

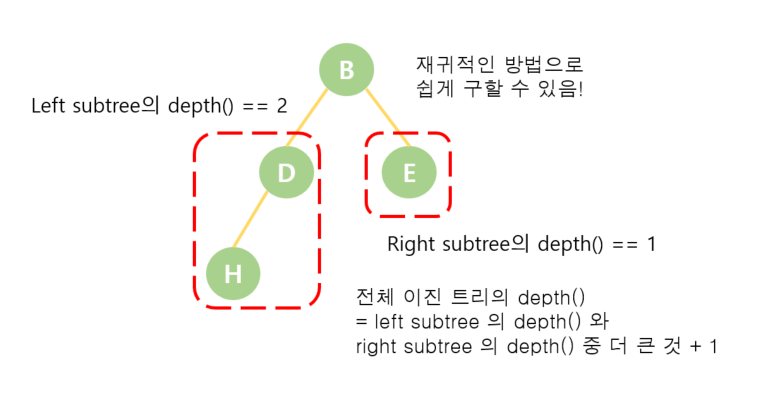
# 이진트리의 구현 - 노드(node)
class Node:
    # 생성자
    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None
        
    # 노드의 갯수 구하는 함수 - 재귀함수 이용
    def size(self):
        l = self.left.size() if self.left else 0
        r = self.right.size() if self.right else 0
        return l + r + 1
    
    # depth
    def depth(self):
        l = self.left.depth() if self.left else 0
        r = self.right.depth() if self.right else 0
        return max(l,r) + 1
    
    # 중위 순회
    def inorder(self):
        traversal = []
        
        # 왼쪽 서브트리가 존재한다면
        if self.left:
            traversal += self.left.inorder()
        
        traversal.append(self.data)
        
        # 오른쪽 서브트리가 있다면
        if self.right:
            traversal += self.right.inorder()
            
        return traversal
        

# 이진 트리의 구현 - 트리(tree)
class BinaryTree:
    # 생성자
    def __init__(self, r):
        self.root = r
        
    # 크기 구하기
    def size(self):
        # 루트가 존재하면 리턴
        if self.root:
            return self.root.size()
        else:
            return 0
        
    # depth
    def depth(self):
        if self.root:
            return self.root.depth()
        else:
            return 0
            
        
    # 중위 순회
    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []

이진 트리의 순회(Traversal)

• 깊이 우선 순회(depth first traversal)

  • 중위 순회(in-order traversal)
  • 전위 순회(pre-order traversal)
  • 후위 순회(post-order traversal)

• 넓이 우선 순회(breadth first traversal)

중위 순회(in-order traversal)

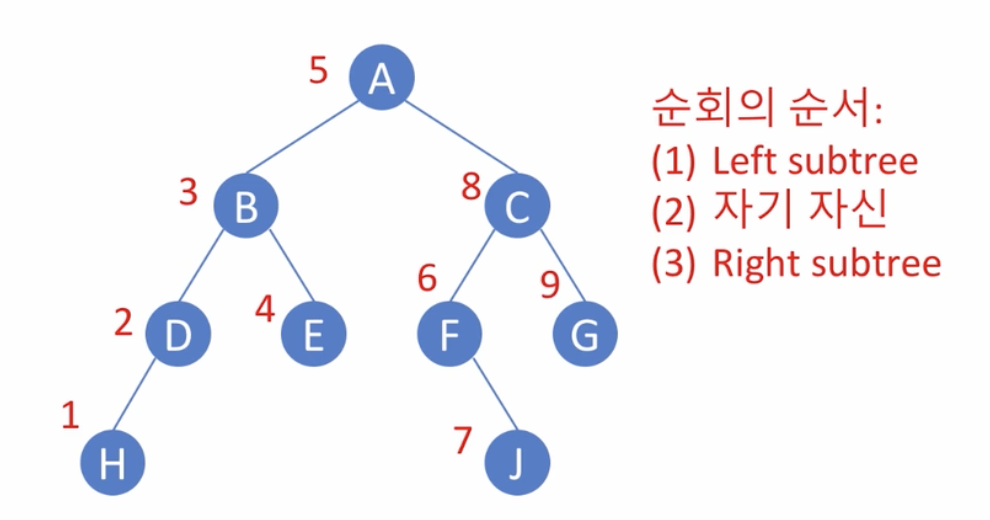
• 방문순서 : H → D → B → E → A → F → J → C → G

# 중위 순회
def inorder(self):
    traversal = []
    
    # 왼쪽 서브트리가 존재한다면
    if self.left:
        traversal += self.left.inorder()
    
    traversal.append(self.data) # 자기 자신을 넣음
    
    # 오른쪽 서브트리가 있다면
    if self.right:
        traversal += self.right.inorder()
        
    return traversal

# 이진 트리의 구현 - 트리(tree)
class BinaryTree:
    # 생성자
    def __init__(self, r):
        self.root = r
        
    # 크기 구하기
    def size(self):
        # 루트가 존재하면 리턴
        if self.root:
            return self.root.size()
        else:
            return 0
        
    # depth
    def depth(self):
        if self.root:
            return self.root.depth()
        else:
            return 0
            
        
    # 중위 순회
    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []

전위 순회(Pre-order Traversal)

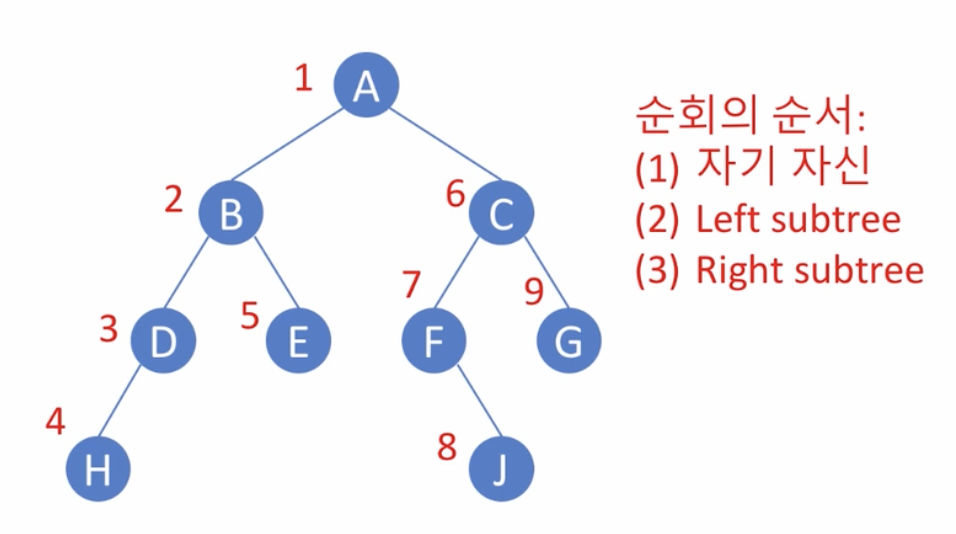
• 방문순서 : A → B → D → H → E → C → F → J → G

후위 순회(Post-order Traversal)

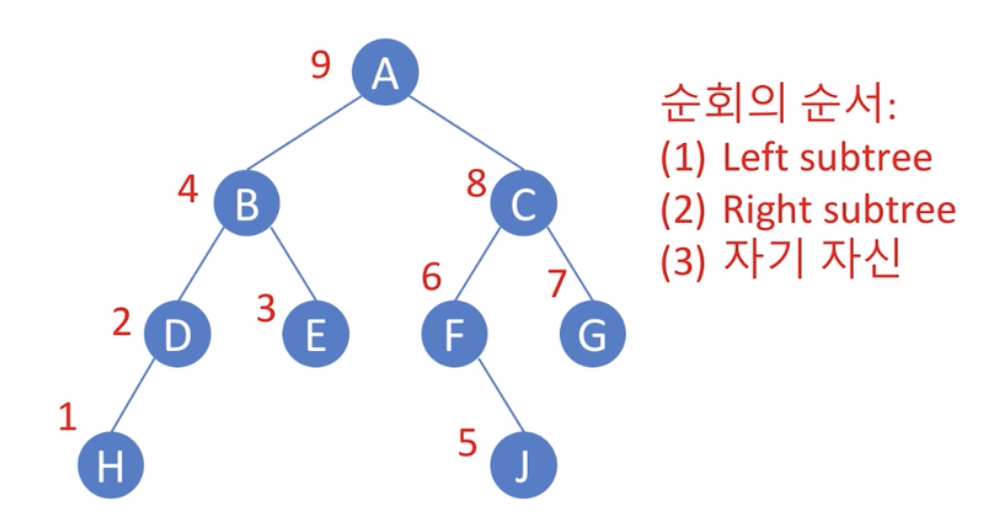
• 방문순서 : H → D → E → B → J → F → G → C → A

[실습_1] 이진트리의 depth() 연산 구현

문제

어서와! 자료구조와 알고리즘은 처음이지? 18강 실습:(1)이진트리의 depth() 연산 구현

문제 설명

이미 주어진 코드 (class Node 와 class BinaryTree 에 의하여) 의 구조를 따르는 이진 트리 (binary tree) 에 대하여, 트리의 깊이 (depth) 를 구하는 연산의 구현을 완성하세요.

초기 코드에 pass 로만 되어 있는 class Node 의 depth() 메서드와 class BinaryTree 의 depth() 메서드를 구현합니다. 코드의 다른 부분은 수정할 필요가 없습니다.

참고로 할 수 있도록, 강의에서 소개한 size() 메서드들 (class Node 와 class BinaryTree 에 대해서) 을 그대로 두었습니다. 문제로 주어진 depth() 연산도 매우 비슷한 식으로 구현할 수 있으니 참고로 삼으세요.

[참고] 실행 을 눌렀을 때 통과하는 것은 아무 의미 없습니다.또한, solution() 함수는 테스트에 영향을 미치므로 수정하지 말고 그대로 두세요.

---

나의 풀이

solution.py

class Node:

    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None

    def size(self):
        l = self.left.size() if self.left else 0
        r = self.right.size() if self.right else 0
        return l + r + 1

    def depth(self):
        l = self.left.depth() if self.left else 0
        r = self.right.depth() if self.right else 0
        return max(l,r) + 1

class BinaryTree:

    def __init__(self, r):
        self.root = r

    def size(self):
        if self.root:
            return self.root.size()
        else:
            return 0

    def depth(self):
        if self.root:
            return self.root.depth()
        else:
            return 0

def solution(x):
    return 0

[실습_2] 이진트리의 전위순회 연산 구현

문제

어서와! 자료구조와 알고리즘은 처음이지? 18강 실습: (2)이진트리의 전위순회 연산 구현

문제 설명

이미 주어진 코드 (class Node 와 class BinaryTree 에 의하여) 의 구조를 따르는 이진 트리 (binary tree) 에 대하여, 트리를 전위 순회 (preorder traversal) 하는 연산의 구현을 완성하세요.

초기 코드에 pass 로만 되어 있는 class Node 의 preorder() 메서드와 class BinaryTree 의 preorder() 메서드를 구현합니다. 코드의 다른 부분은 수정할 필요가 없습니다.

참고로 할 수 있도록, 강의에서 소개한 inorder() 메서드들 (class Node 와 class BinaryTree 에 대해서) 을 그대로 두었습니다. 문제로 주어진 preorder() 연산도 매우 비슷한 식으로 구현할 수 있으니 참고로 삼으세요.

[참고] 실행 을 눌렀을 때 통과하는 것은 아무 의미 없습니다.또한, solution() 함수는 테스트에 영향을 미치므로 수정하지 말고 그대로 두세요.

---

나의 풀이

solution.py

class Node:

    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None

    def inorder(self):
        traversal = []
        if self.left:
            traversal += self.left.inorder()
        traversal.append(self.data)
        if self.right:
            traversal += self.right.inorder()
        return traversal

    def preorder(self):
        traversal = []
        traversal.append(self.data)
        if self.left:
            traversal += self.left.preorder()
        if self.right:
            traversal += self.right.preorder()
        return traversal

class BinaryTree:

    def __init__(self, r):
        self.root = r

    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []

    def preorder(self):
        if self.root:
            return self.root.preorder()
        else:
            return []

def solution(x):
    return 0

[실습_3] 이진트리의 후위순회 연산 구현

문제

어서와! 자료구조와 알고리즘은 처음이지?18강 실습: (3)이진트리의 후위순회 연산 구현

문제 설명

이미 주어진 코드 (class Node 와 class BinaryTree 에 의하여) 의 구조를 따르는 이진 트리 (binary tree) 에 대하여, 트리를 후위 순회 (postorder traversal) 하는 연산의 구현을 완성하세요.

초기 코드에 pass 로만 되어 있는 class Node 의 postorder() 메서드와 class BinaryTree 의 postorder() 메서드를 구현합니다. 코드의 다른 부분은 수정할 필요가 없습니다.

참고로 할 수 있도록, 강의에서 소개한 inorder() 메서드들 (class Node 와 class BinaryTree 에 대해서) 을 그대로 두었습니다. 문제로 주어진 postorder() 연산도 매우 비슷한 식으로 구현할 수 있으니 참고로 삼으세요.

[참고] 실행 을 눌렀을 때 통과하는 것은 아무 의미 없습니다.또한, solution() 함수는 테스트에 영향을 미치므로 수정하지 말고 그대로 두세요.

---

나의 풀이

solution.py

class Node:

    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None

    def inorder(self):
        traversal = []
        if self.left:
            traversal += self.left.inorder()
        traversal.append(self.data)
        if self.right:
            traversal += self.right.inorder()
        return traversal

    def postorder(self):
        traversal = []
        if self.left:
            traversal += self.left.postorder()
        if self.right:
            traversal += self.right.postorder()
        traversal.append(self.data)
        return traversal

class BinaryTree:

    def __init__(self, r):
        self.root = r

    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []

    def postorder(self):
        if self.root:
            return self.root.postorder()
        else:
            return []

def solution(x):
    return 0