이진 탐색 트리에서 원소 삭제

• 키(key)를 이용해서 노드를 찾는다
• 만약 해당 키의 노드가 없으면 삭제할 것이 없음
• 노드가 있으면 찾은 노드의 부모 노드도 알고 있어야 함
• 찾은 노드를 제거하고도 이진 탐색 트리 성질을 만족하도록 트리의 구조를 정리

원소 삭제의 인터페이스 설계

• 입력 : 키(key)
• 리턴(출력)
• 삭제한 경우 : True
• 해당 키의 노드가 없는 경우 False

이진 탐색 트리 구조의 유지

• 삭제된 노드 대상
  
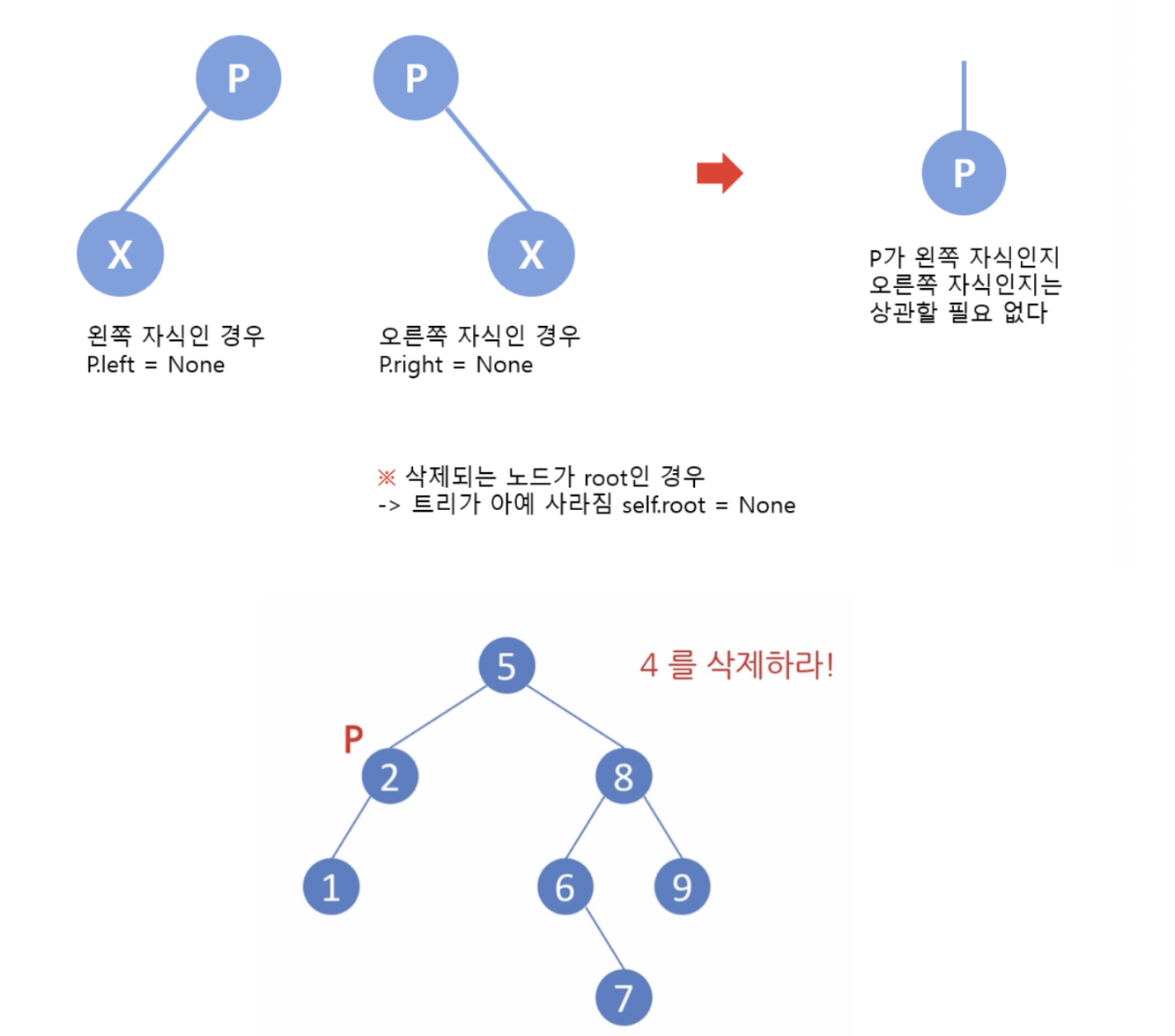
• 원소 삭제의 경우 1 - 말단(leaf)노드인 경우
  • 해당 노드만 삭제
  • 부모 노드의 링크 조정(왼쪽 또는 오른쪽)

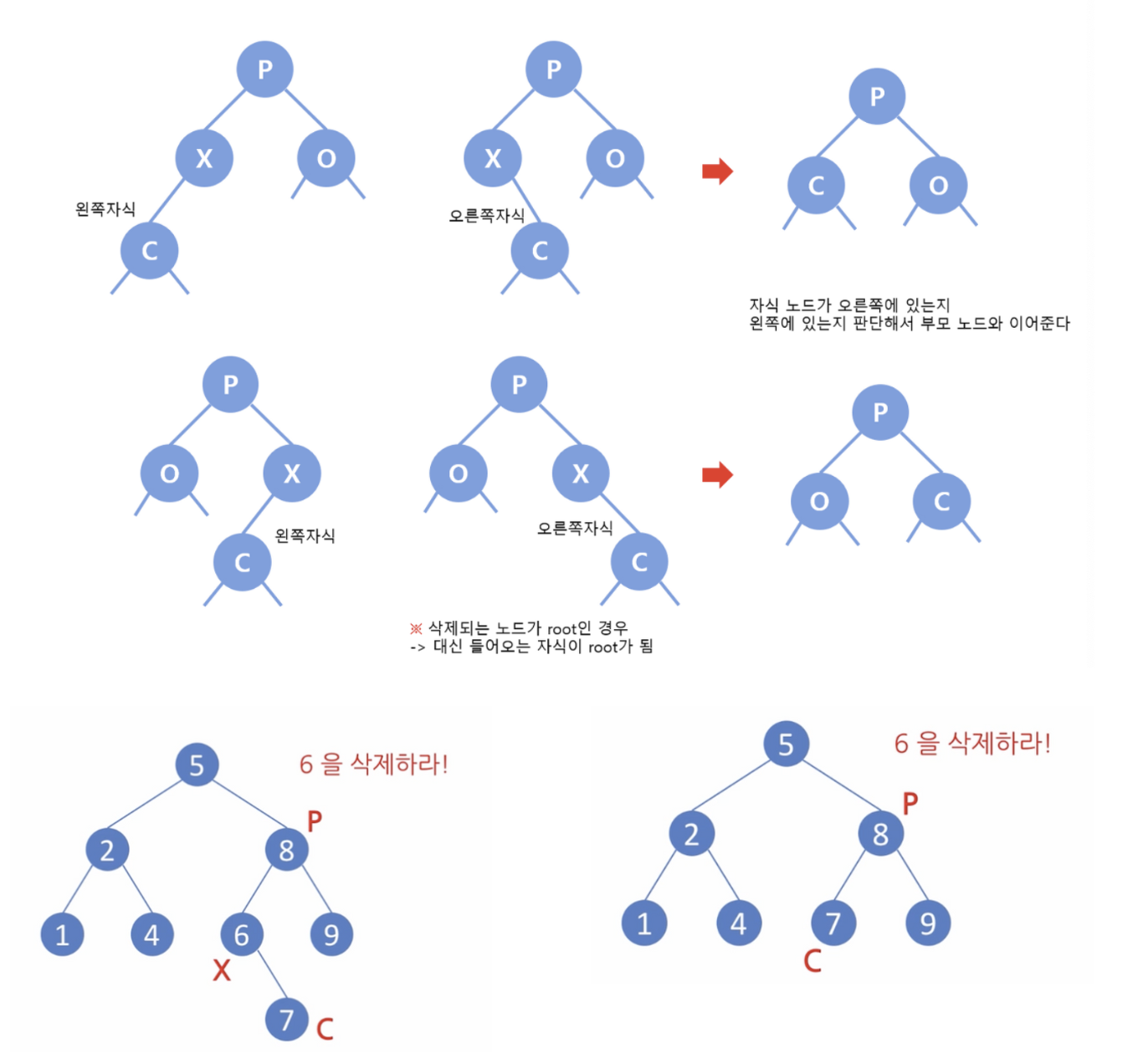
• 원소 삭제의 경우 2 - 자식을 하나 가지고 있는 경우

  • 삭제되는 노드 자리에 그 자식을 대신 배치

  • 자식이 왼쪽인지 오른쪽인지

  • 부모 노드의 링크를 조정(왼쪽 또는 오른쪽)

  • 삭제되는 노드가 root인 경우

    → 대신 들어오는 자식노드가 root가 됨

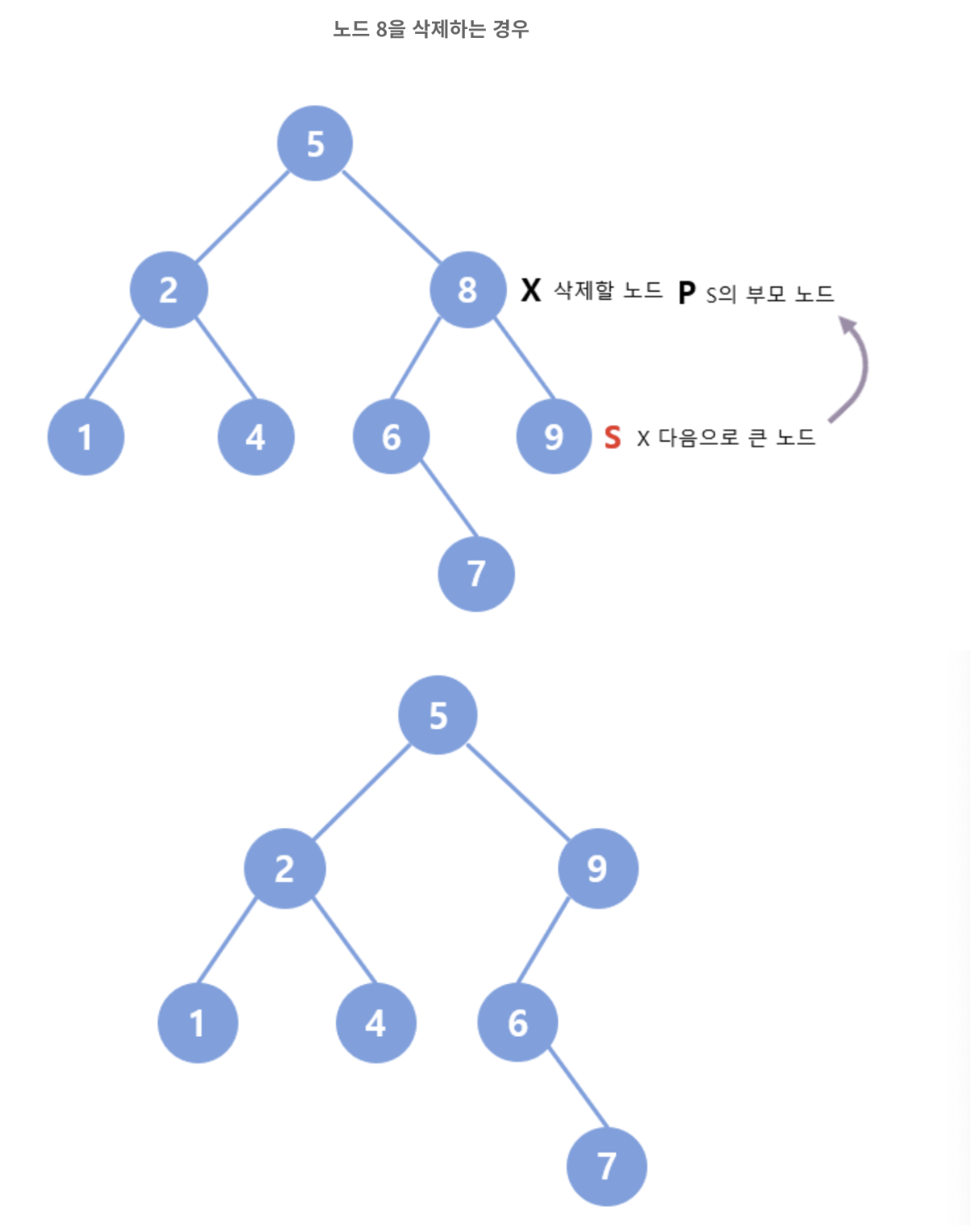
• 원소 삭제의 경우 3 - 자식을 둘을 가지고 있는 경우
  • 삭제되는 노드보다 바로 다음 큰 키를 가지는 노드를 찾아 그 노드를 삭제되는 노드 자리에 대신 배치 그리고 해당 노드를 삭제

코드 구현

class Node:
    # 자식을 세어보자
    def countChildren(self):
        count = 0
        if self.left:
            count += 1
        if self.right:
            count += 1
        return count
        
        
class BinSearchTree:
    # 노드 삭제
    def remove(self, key):
        # 삭제하려는 노드와 p를 검색
        node, parent = self.lookup(key)

        # 삭제하려는 노드가 존재하면
        if node:
            # 자식노드의 개수가 몇개 있는지 확인
            nChildren = node.countChildren()

            # The simplest case of no children
            if nChildren == 0:
                # 만약 parent 가 있으면 (루트노드가 아니란소리)
                # node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
                # parent.left 또는 parent.right 를 None 으로 하여
                # leaf node 였던 자식을 트리에서 끊어내어 없앱니다.
                if parent:
                    if parent.left == node:
                        parent.left = None
                    if parent.right == node:
                        parent.right = None

                # 만약 parent 가 없으면 (node 는 root 인 경우)
                # self.root 를 None 으로 하여 빈 트리로 만듭니다.
                else:
                    self.root = None

            # When the node has only one child
            elif nChildren == 1:
                # 하나 있는 자식이 왼쪽인지 오른쪽인지를 판단하여
                # 그 자식을 어떤 변수가 가리키도록 합니다.
                if node.left:
                    temp = node.left
                else:
                    temp = node.right

                # 만약 parent 가 있으면
                # node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
                # 위에서 가리킨 자식을 대신 node 의 자리에 넣습니다.
                if parent:
                    if parent.left == node:
                        parent.left = temp
                    else:
                        parent.right = temp
                
                # 만약 parent 가 없으면 (node 는 root 인 경우)
                # self.root 에 위에서 가리킨 자식을 대신 넣습니다.
                else:
                    self.root = temp
            
            # When the node has both left and right children
            else:
                parent = node
                successor = node.right
                # parent 는 node 를 가리키고 있고,
                # successor 는 node 의 오른쪽 자식을 가리키고 있으므로
                # successor 로부터 왼쪽 자식의 링크를 반복하여 따라감으로써
                # 순환문이 종료할 때 successor 는 바로 다음 키를 가진 노드를,
                # 그리고 parent 는 그 노드의 부모 노드를 가리키도록 찾아냅니다.
                while successor.left:
                    parent = successor
                    successor = successor.left
                
                # 삭제하려는 노드인 node 에 successor 의 key 와 data 를 대입합니다.
                node.key = successor.key
                node.data = successor.data

                # 이제, successor 가 parent 의 왼쪽 자식인지 오른쪽 자식인지를 판단하여
                # 그에 따라 parent.left 또는 parent.right 를
                # successor 가 가지고 있던 (없을 수도 있지만) 자식을 가리키도록 합니다.
                if parent.left == successor:
                    parent.left = successor.right
                else:
                    parent.right = successor.right
                    

            return True

        else:
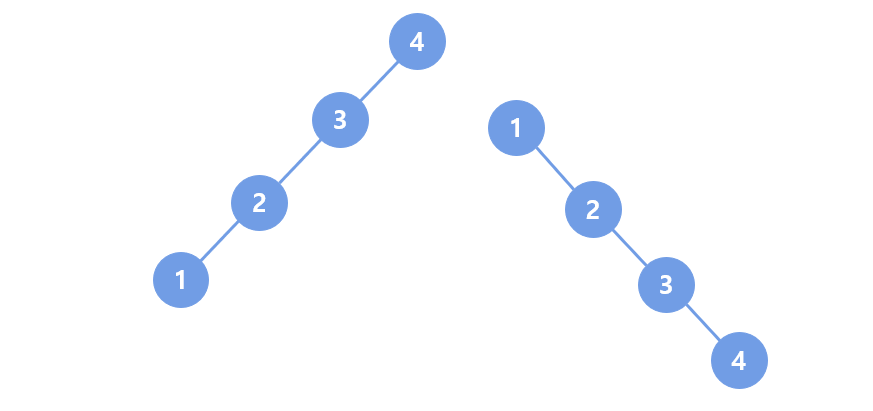
            return False

이진트리가 효육적이지 못한 경우

• 순서대로 삽입하는 경우 효율적이지 못하다
• 한쪽으로 치우치는 모양

참고 - 보다 나은 성능을 보이는 이진 탐색 트리들

• 높이의 균형을 유지함으로써 O(logN)의 탐색 복잡도를 보장
• 삽입, 삭제 연산이 보다 복잡해짐

AVL tree

AVL 트리

Red black tree

레드-블랙 트리

[실습] 이진 탐색 트리에서 노드의 삭제 연산 구현

문제

어서와! 자료구조와 알고리즘은 처음이지? 21강 실습: 이진 탐색 트리에서 노드의 삭제 연산 구현

문제 설명

초기 코드에 주어진 class Node 와 class BinSearchTree 를 기반으로, 이진 탐색 트리 (binary search tree) 에서 지정된 원소를 삭제하는 remove(key) 연산의 구현을 완성하세요.

class Node 와 class BinSearchTree 에 이미 구현되어 있는 코드는 수정하지 마세요. 코드 구현의 정확성 평가에 이용됩니다. 초기 코드에 들어 있는 주석을 참고로 하여, BinSearchTree::remove() 메서드의 안에 들어 있는 pass 를 없애고 그 자리에 올바른 코드를 써 넣으면 됩니다.

[참고 1] solution() 함수의 구현은 그대로 두세요. 이것을 없애면 테스트가 되지 않습니다.

[참고 2] 코드 실행 을 눌렀을 때 통과하는 것은 아무런 의미가 없습니다.

[참고 3] 잘 생각해 보면, 이진 탐색 트리를 구현하지 않고 키 순서대로 정렬된 Python 의 배열을 유지함으로써도 같은 연산을 구현할 수 있습니다. 이 연습문제에서는 효율성 테스트를 하지 않기 때문에 이러한 구현을 오답으로 간주하지 않습니다만, 배열을 이용한 구현과 트리 구조를 이용한 구현은 연산의 복잡도에 큰 차이가 있습니다. 이진 탐색 트리로 구현하여 코드 작성 연습을 하시기 바랍니다.

*** 2020년 2월 3일에 테스트 케이스가 미비했음이 발견되어 하나의 테스트 케이스 (8번) 를 추가했습니다.

---

나의 풀이

solution.py

class Node:

    def __init__(self, key, data):
        self.key = key
        self.data = data
        self.left = None
        self.right = None

    def insert(self, key, data):
        if key < self.key:
            if self.left:
                self.left.insert(key, data)
            else:
                self.left = Node(key, data)
        elif key > self.key:
            if self.right:
                self.right.insert(key, data)
            else:
                self.right = Node(key, data)
        else:
            raise KeyError('Key %s already exists.' % key)

    def lookup(self, key, parent=None):
        if key < self.key:
            if self.left:
                return self.left.lookup(key, self)
            else:
                return None, None
        elif key > self.key:
            if self.right:
                return self.right.lookup(key, self)
            else:
                return None, None
        else:
            return self, parent

    def inorder(self):
        traversal = []
        if self.left:
            traversal += self.left.inorder()
        traversal.append(self)
        if self.right:
            traversal += self.right.inorder()
        return traversal

    def countChildren(self):
        count = 0
        if self.left:
            count += 1
        if self.right:
            count += 1
        return count

class BinSearchTree:

    def __init__(self):
        self.root = None

    def insert(self, key, data):
        if self.root:
            self.root.insert(key, data)
        else:
            self.root = Node(key, data)

    def lookup(self, key):
        if self.root:
            return self.root.lookup(key)
        else:
            return None, None

    def remove(self, key):
        node, parent = self.lookup(key)
        if node:
            nChildren = node.countChildren()
            # The simplest case of no children
            if nChildren == 0:
                # 만약 parent 가 있으면
                # node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
                # parent.left 또는 parent.right 를 None 으로 하여
                # leaf node 였던 자식을 트리에서 끊어내어 없앱니다.
                if parent:
                    if parent.left == node:
                        parent.left = None
                    if parent.right == node:
                        parent.right = None
                # 만약 parent 가 없으면 (node 는 root 인 경우)
                # self.root 를 None 으로 하여 빈 트리로 만듭니다.
                else:
                    self.root = None
            # When the node has only one child
            elif nChildren == 1:
                # 하나 있는 자식이 왼쪽인지 오른쪽인지를 판단하여
                # 그 자식을 어떤 변수가 가리키도록 합니다.
                if node.left:
                    temp = node.left
                else:
                    temp = node.right
                # 만약 parent 가 있으면
                # node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
                # 위에서 가리킨 자식을 대신 node 의 자리에 넣습니다.
                if parent:
                    if parent.left == node:
                        parent.left = temp
                    else:
                        parent.right = temp
                # 만약 parent 가 없으면 (node 는 root 인 경우)
                # self.root 에 위에서 가리킨 자식을 대신 넣습니다.
                else:
                    self.root = temp
            # When the node has both left and right children
            else:
                parent = node
                successor = node.right
                # parent 는 node 를 가리키고 있고,
                # successor 는 node 의 오른쪽 자식을 가리키고 있으므로
                # successor 로부터 왼쪽 자식의 링크를 반복하여 따라감으로써
                # 순환문이 종료할 때 successor 는 바로 다음 키를 가진 노드를,
                # 그리고 parent 는 그 노드의 부모 노드를 가리키도록 찾아냅니다.
                while successor.left:
                    parent = successor
                    successor = successor.left
                # 삭제하려는 노드인 node 에 successor 의 key 와 data 를 대입합니다.
                node.key = successor.key
                node.data = successor.data
                # 이제, successor 가 parent 의 왼쪽 자식인지 오른쪽 자식인지를 판단하여
                # 그에 따라 parent.left 또는 parent.right 를
                # successor 가 가지고 있던 (없을 수도 있지만) 자식을 가리키도록 합니다.
                if parent.left == successor:
                    parent.left = successor.right
                else:
                    parent.right = successor.right

            return True

        else:
            return False

    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []

def solution(x):
    return 0