재귀 함수(Recursive Functions)

• 하나의 함수에서 자신을 다시 호출하여 작업을 수행하는 것
• e.g.
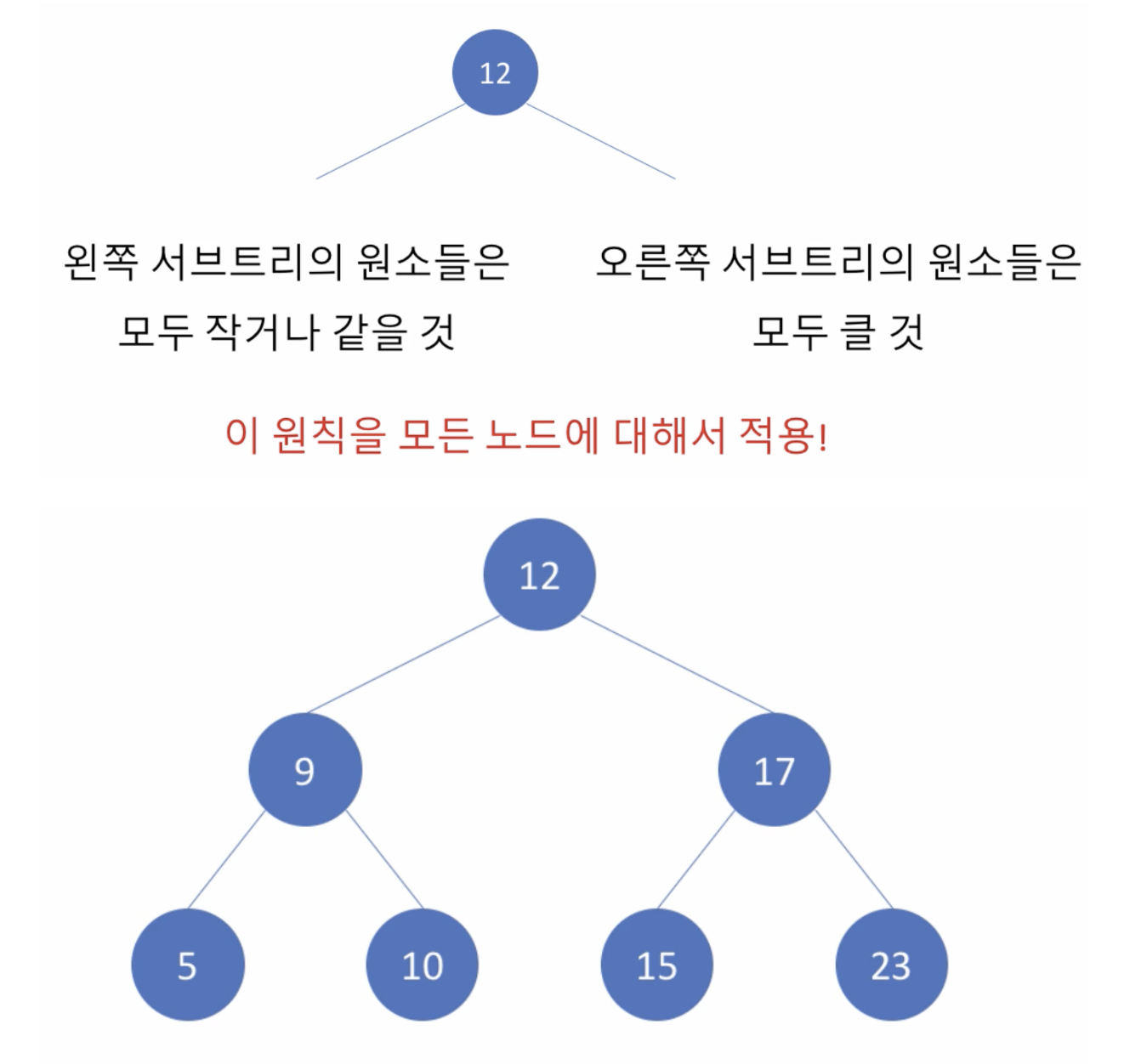
  • 이진 트리(binary trees)

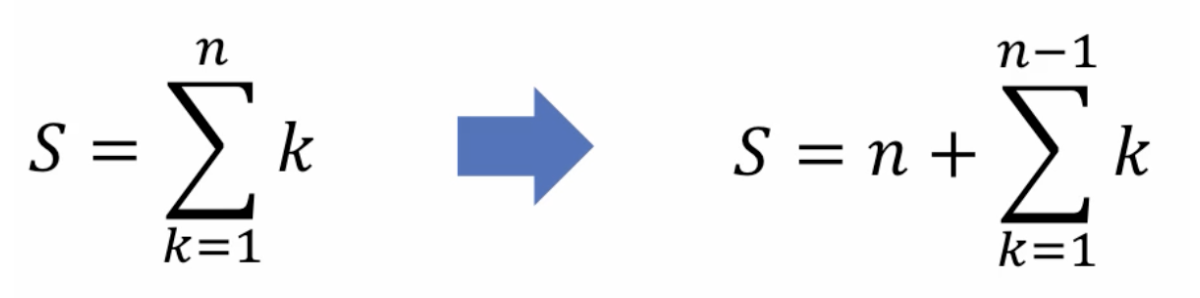
자연수의 합 구하기

• 1부터 n까지의 모든 자연수의 합을 구하기

def sum(n):
# print(n)
	if n <= 1: // 재귀 호출의 종결 조건
    		return n
    	else:
        	return n + sum(n-1)

        a = int(input("Number: "))
        print(sum(a))

• 재귀 호출의 종결 조건
• 알고리즘의 종결조건에 반드시 필요

재귀 알고리즘의 효율

• O(n) 보다 O(1) 더 효율
• 따라서 재귀 함수로 구현 했을 떄와 비교하여 효율을 비교해볼 필요 있음

[실습] 피보나치 순열

참고

Iterative version vs Recursive version

문제

어서와! 자료구조와 알고리즘은 처음이지? 4강 실습: 피보나치 순열

문제 설명

인자로 0 또는 양의 정수인 x 가 주어질 때, Fibonacci 순열의 해당 값을 구하여 반환하는 함수 solution() 을 완성하세요.

Fibonacci 순열은 아래와 같이 정의됩니다.F0 = 0F1 = 1Fn = Fn - 1 + Fn - 2, n >= 2

재귀함수 작성 연습을 의도한 것이므로, 재귀적 방법으로도 프로그래밍해 보고, 반복적 방법으로도 프로그래밍해 보시기 바랍니다.

---

나의 풀이

• F0 = 0 ( n≥2 )
  F1 = 1 ( n≥2 )
  F2 = F1(1) + F0(0) = 1 ( n≥2 )
  F3 = F2(1) + F1(1) = 2 ( n≥2 )
  F4 = F3(2) + F2(1) = 3 ( n≥2 )
  F5 = F4(3) + F3(2) = 5 ( n≥2 )
• 재귀적 방법
  • x = 0 이면,
    • return 0
  • x < 3 이면,
    • return 1
  • x >= 3 이면,
    • return fibo(x-1) + fibo(x-2)

solution.py

def solution(x):
    # answer = 0
    if x == 0:
        return 0
    if x < 3:
        return 1
    else:
        return solution(x-1) + solution(x-2)
    
    return answer

다른 사람의 풀이

• x < 2 이면
  • return x
• else
  • 재귀함수 호출 방식
  • return solution(x-1) + solution(x-2)

solution.py

def solution(x):
    if( x < 2): return x

    answer = solution(x-1) + solution(x-2)
    return answer