[프로그래머스] Lv.1 콜라츠 추측 (JS)

🔎 문제

1937년 Collatz란 사람에 의해 제기된 이 추측은, 주어진 수가 1이 될 때까지 다음 작업을 반복하면, 모든 수를 1로 만들 수 있다는 추측입니다.
작업은 다음과 같습니다.

1-1. 입력된 수가 짝수라면 2로 나눕니다. 
1-2. 입력된 수가 홀수라면 3을 곱하고 1을 더합니다. 
2. 결과로 나온 수에 같은 작업을 1이 될 때까지 반복합니다. 

예를 들어, 주어진 수가 6이라면 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1 이 되어 총 8번 만에 1이 됩니다.
위 작업을 몇 번이나 반복해야 하는지 반환하는 함수, solution을 완성해 주세요.
단, 주어진 수가 1인 경우에는 0을, 작업을 500번 반복할 때까지 1이 되지 않는다면 –1을 반환해 주세요.

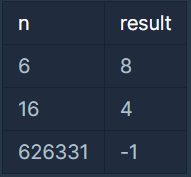
입출력 예

---

🔓 풀이 과정

고민

1) 짝수와 홀수를 구분하여 로직을 짠다
2) 숫자가 1이 되는 시점에 함수를 종료하면서 리턴한다
2) 500번 이상을 돌려주면 -1을 리턴한다
3) 일단 for문 사용해보기

나의 풀이

function solution(num) {
  for (let i = 0; i < 500; i++) {
    if (num % 2 == 0) {
      num = num / 2;
    } else if (num == 1) {
      return i; // 함수 종료 시점 : num이 1이 됐을 때
    } else if (num % 2 == 1) { // 나누었는데 홀수라면 다시 돌리기
      num = num * 3 + 1;
    }
  }
  return -1; // i가 500을 넘어가면 -1 리턴
}
// num이 1인 경우는 따로 설정을 안해도 되는 걸까?

그 밖의 풀이

// 1. 나의 풀이에서 삼항 연산자를 사용함
function solution(num) {
  let answer = 0;
  for (let i = 0; i < 500; i++) {
    if (num != 1) {
      num = num % 2 == 0 ? num / 2 : num * 3 + 1;
    } else {
      return (answer = i);
    }
  }
  return (answer = -1);
}

// 2. while문 사용
function solution(num) {
  let answer = 0;
  while (num != 1 && answer != 500) {
    num % 2 == 0 ? (num = num / 2) : (num = num * 3 + 1);
    answer++;
  }
  return num == 1 ? answer : -1;
}
 // 1이 되면 누적된 answer를, 누적된 answer가 500이 넘으면 -1 리턴