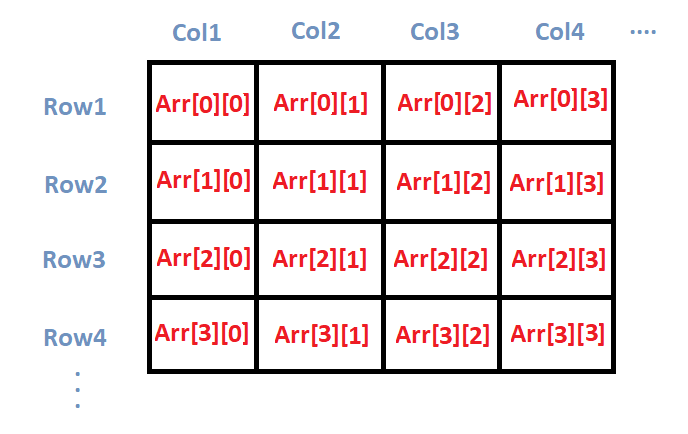
1. 2차원 배열이란?
2차원 배열은 행렬과 같이 2차원으로 구성된 배열을 의미한다.
물론, 실제로 위의 그림과 같은 2차원 메모리 구조를 갖는 것이 아닌, 시스템적으로 2차원 처럼 구현된 구조이다.
1.1 2차원 배열의 구조
java에서는 2차원 혹은 2차원 이상의 다차원 배열을 생성할때 메모리는
배열의 배열형식으로 할당이 된다.
다차원 배열을 생성하면 메모리 상에서 다음과 같이 연속적인 형태로 할당될 것이라 생각하고 있을 것이다.
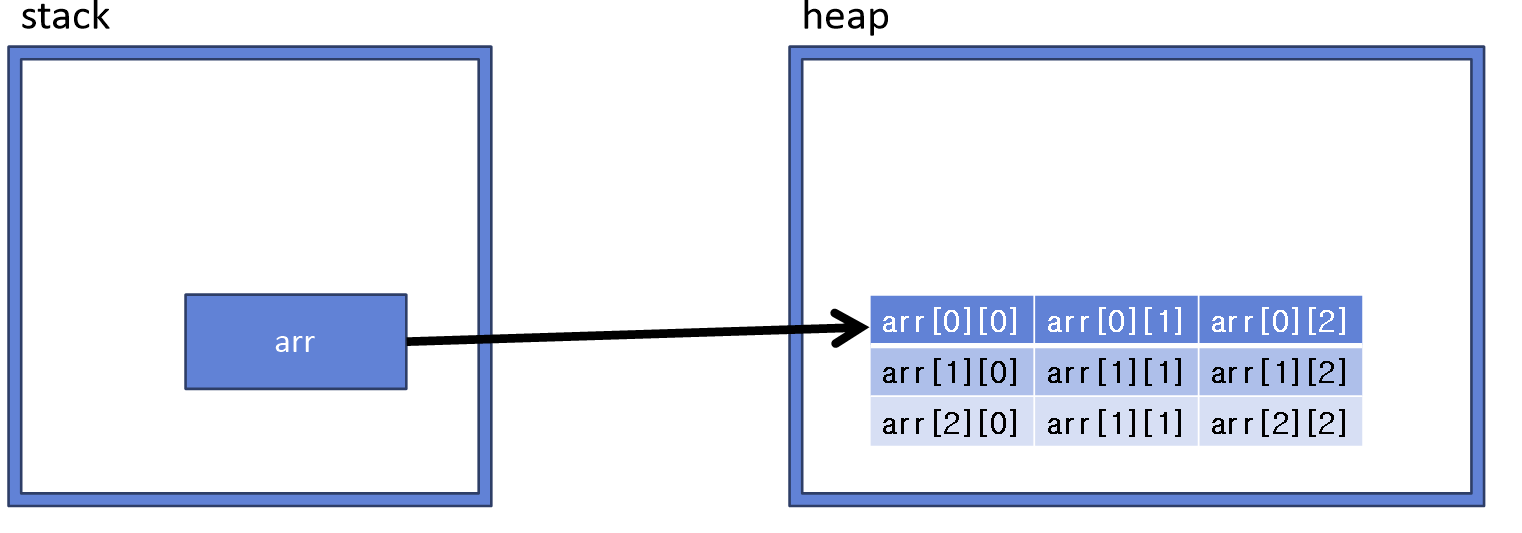
실제로 C언어 등의 많은 언어에서도 이와 같은 방식을 채택하고 있다.
그러나, java의 경우 이와 다른 방식으로 메모리가 할당이 된다.
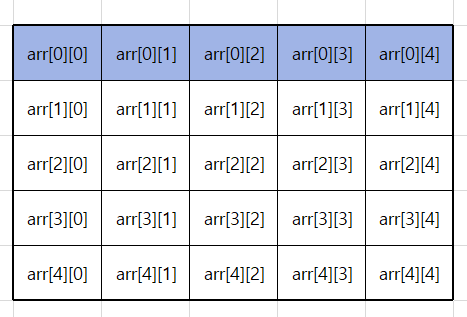
java 의 경우 다차원 배열의 경우 아래 그림과 같은 배열의 배열 형식으로 구성되 있다.
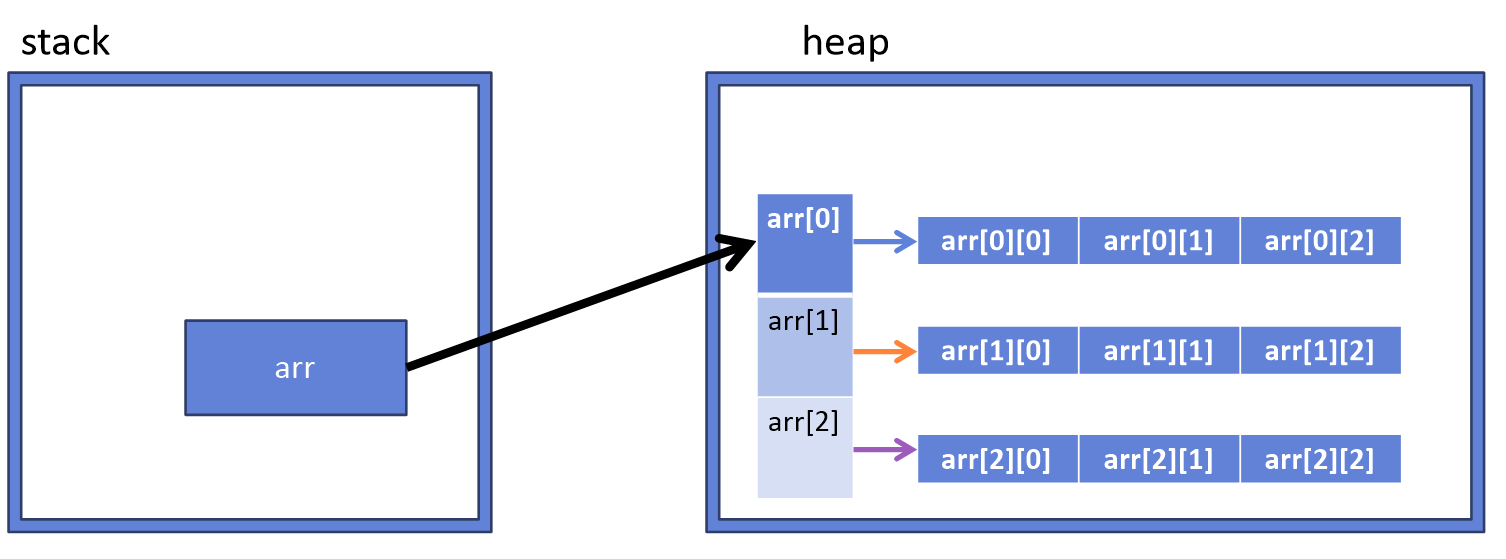
이를 즉, arr[0], arr[1], arr[2]에는 값이 아니라 각 1차원 배열의 주소가 저장되 있다. 이를 조금 더 쉽게 이해하기 위해 코드로 나타내면 다음과 같다.
/*1번*/
int arr[][] = new int[3][3]; //3*3 배열 생성
/*2번*/
int arr[][]= new int[3][];// 3*x 배열 생성
arr[0]=new int[3];
arr[1]=new int[3];
arr[2]=new int[3];위 코드의 1번과 2번은 완전히 동일한 3*3 배열이다.
이와같이 java에서 2차원 이상의 배열에서는 배열의 배열 형태로 메모리가 할당이 된다.
1.2 가변배열
가변배열이란 다차원 배열에서 각 배열의 크기가 다른 배열을 의미한다.
2차원 혹은 다차원 배열의 경우 배열의 배열 이라는 형태로 배열이 생성이 된다. 이러한 배열의 배열특징을 이용하면 아래와 같은 배열 역시 만들 수 있다.
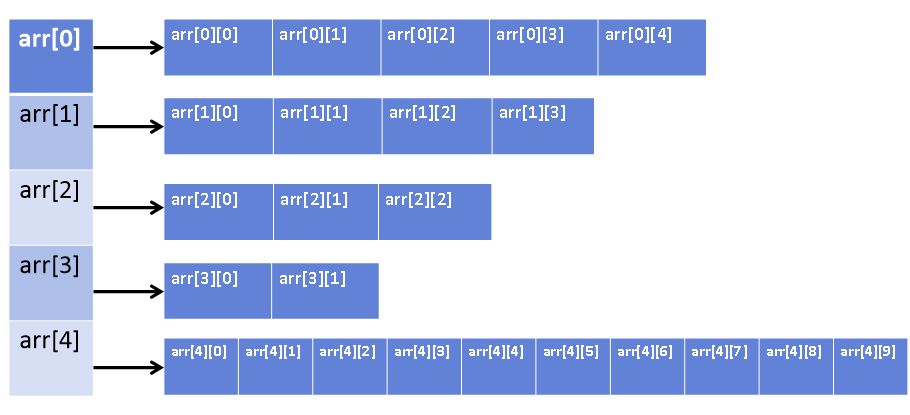
위의 배열 역시 각 배열의 크기가 다르긴 하지만 배열의 배열형태이므로 2차원 배열임은 동일하다.
이렇듯, 각 배열의 크기가 다른 배열을 가변배열 이라고 한다.
2. 2차원 배열의 선언 및 초기화
2.1 2차원 배열의 선언
2차원 배열의 선언은 다음과 같이 2가지 방식으로 선언이 가능하다.
자료형[][] 배열이름;// 선언방법 1 자료형 배열이름[][];// 선언방법 2
또한, 배열을 생성하기 위해서는 1차원 배열과 마찬가지로 new 키워드를 사용해서 생성하면 된다.
예를 들어 int형의 4*3배열을 선언하고자 하면 다음과 같이 코드를 작성하면 된다.
int[][] arr=new int[4][3];혹은
int arr[][]=new int[4][3];이렇게 코드를 작성하면 아래 표와 같은 4*3 배열이 생성이 된다.

2.2 2차원 배열의 초기화
2차원 배열을 초기화는 중괄호를 2개 사용해 초기화를 한다.
2차원 배열의 초기화는 1차원 배열의 초기화아 비슷하게 중괄호를 사용해 초기화를 할 수 있다.
다만, 다음과 같이 중괄호 2개를 사용해 초기화를 한다.
int arr[][]= {
{10, 20, 50},// arr[0][0] ~ arr[0][2] 초기화
{20, 30, 5},// arr[1][0] ~ arr[1][2] 초기화
{50, 7, 100}// arr[2][0] ~ arr[2][2] 초기화
};그 외에도 규칙이 있는 경우 아래와 같이 반복문을 사용해 초기화를 할 수 있다.
import java.util.Arrays;
public class Array2D {
public static void main(String[] args) {
int i, j;
int data=10;
int arr[][]= new int[5][5];
for(i=0; i<arr.length; i++) {
for(j=0; j<arr[i].length; j++) {
arr[i][j]=data;
data+=10;
}
}
for(i=0; i<arr.length; i++) {
System.out.println(Arrays.toString(arr[i]));
}
}
}output
[10, 20, 30, 40, 50]
[60, 70, 80, 90, 100]
[110, 120, 130, 140, 150]
[160, 170, 180, 190, 200]
[210, 220, 230, 240, 250]위의 코드를 보면 조금 이상한 부분이 있을 것이다. 분명 5*5 배열이라 arr.length가 25이 될 것이라 예상했지만 실제로는 5가 됬다.
arr.length는 전체 배열의 길이를 담고 있는 것이 아니다. 정확히 말하면 arr 번지에 있는 1차원 배열의 길이가 담겨있는 것이다.
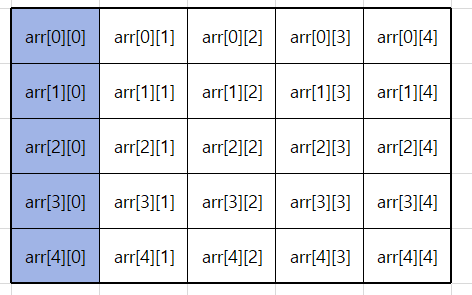
아래는 5*5 배열의 정확한 구조이다.

앞서 설명한 바와 같이 java에서 다차원 배열은 1차원 배열을 이용한 배열의 배열형태이다. 즉, arr.length의 경우 다음과 같은 배열의 크기를 의미한다.
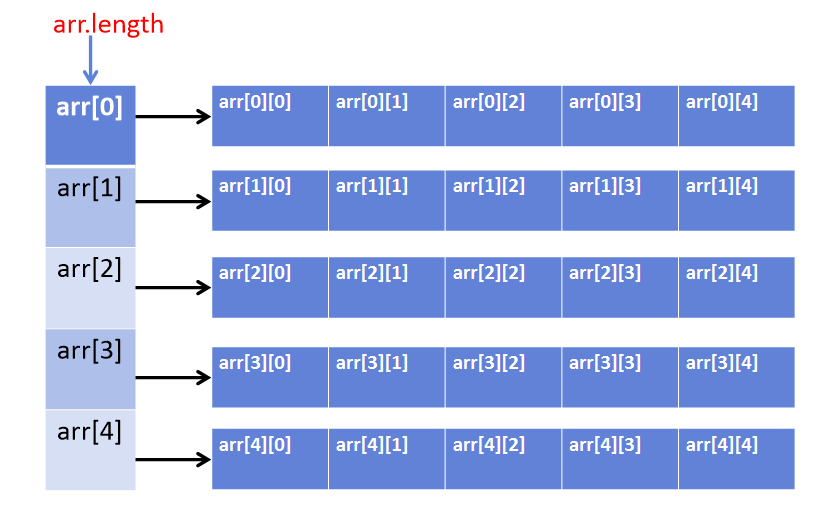
이와 같이 다차원 배열에서 .length를 사용할 경우에는 모든 배열의 크기를 나타내는 것이 아님을 고려해 사용해야 한다.
3. 2차원 배열의 활용
3.1 빙고
2차원 배열을 활용해 빙고게임을 할 수 있다.
다음과 같은 빙고판이 있다고 가정하자.
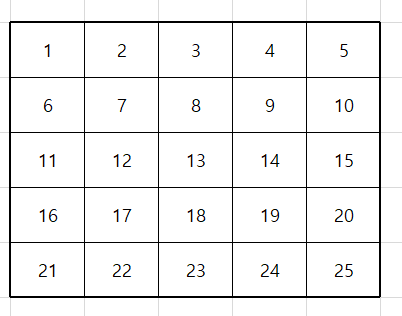
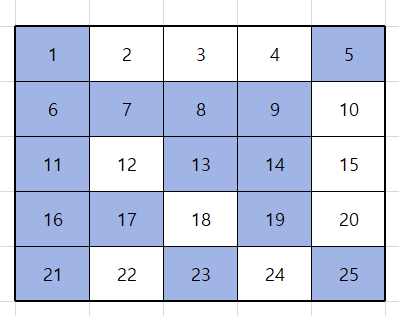
게임을 진행하면서 빙고판에 숫자를 불러 아래와 같이 색칠한 빙고판이 됬다고 가정하자.
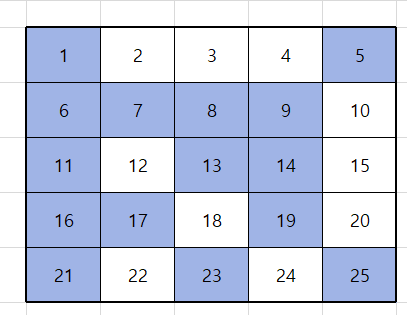
이때, 이 게임에서의 빙고의 갯수를 구하는 방법은 다음과 같다.
- 가로줄 빙고 조건
가로줄이 빙고가 되려면 다음과 같이 가로 한 줄 전부가 색칠이 되 있어야 한다.
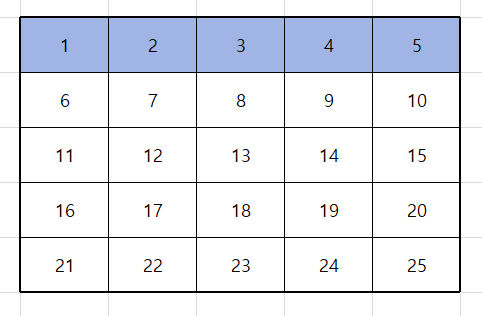
쉬운 해석을 위해 빙고 안에 있는 숫자를 배열의 위치로 나타내면 아래 그림과 같다.
빙고판을 보면 2차원 배열의 가로 부분이 전부 색칠되 있으면 빙고임을 알 수 있다.
이를 기반으로 색칠된 부분은 숫자 0이 채워져 있다는 가정하에 가로줄 빙고 확인 코드를 작성하면 다음과 같다.
for(int i=0; i<5; i++) {// 다음줄
for(int j=0; j<5; j++) {
if(arr[i][j]==0) {// 가로 1칸이 색칠되 있는 경우
colorCnt++;// 색칠된 카운트 증가
}
}
if(colorCnt==5) {// 색칠된 카운트=빙고판 가로칸 갯수
bingoCnt++;// 빙고
}
colorCnt=0;// 색칠된 부분 카운트 초기화
}- 세로줄 빙고 조건
세로줄이 빙고가 되려면 다음과 같이 세로 한 줄 전부가 색칠이 되 있어야 한다.
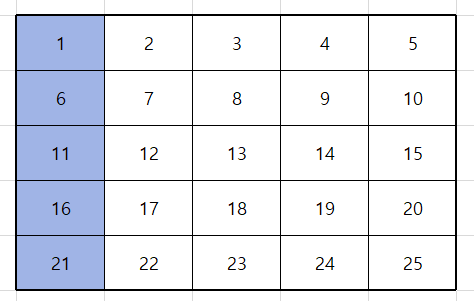
쉬운 해석을 위해 빙고 안에 있는 숫자를 배열의 위치로 나타내면 아래 그림과 같다.
빙고판을 보면 2차원 배열의 세로 부분이 전부 색칠되 있으면 빙고임을 알 수 있다.
이를 기반으로 가로줄 빙고 확인 코드를 작성하면 다음과 같다.
for(int i=0; i<5; i++) {// 다음줄
for(int j=0; j<5; j++) {
if(arr[j][i]==0) {// 세로 1칸이 색칠되 있는 경우
colorCnt++;// 색칠된 카운트 증가
}
}
if(colorCnt==5) {// 색칠된 카운트=빙고판 세로칸 갯수
bingoCnt++;// 빙고
}
colorCnt=0;// 색칠된 부분 카운트 초기화
}가로줄과 코드가 비슷하나, 유의해야 할 부분은 가로줄의 빙고는 arr[i][j]였으나, 세로줄의 빙고는 arr[j][i]이다.
- 대각선 빙고 조건
대각선의 경우, 아래 그림과 같이 왼쪽 위->오른쪽 아래 부분으로 빙고와, 오른쪽 위->왼쪽 아래 부분으로 빙고 이렇게 2가지의 빙고 방법이 있다.
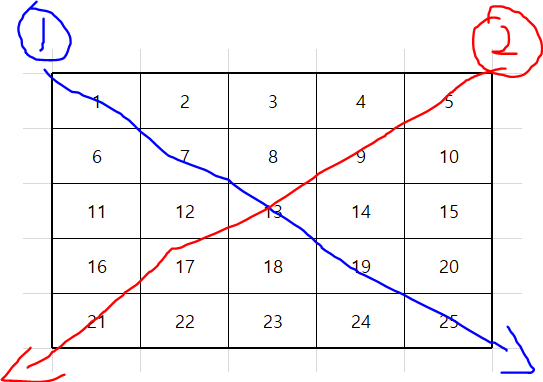
먼저, 왼쪽 위->오른쪽 아래 부분의 빙고를 배열의 위치로 보면 다음과 같다.
배열의 위치를 유심히 살펴보면arr[0][0]부터arr[4][4]까지 배열의 가로와 세로 위치가 각각 1씩 증가하는 위치에 색칠이 칠해진 것을 볼 수 있다.
이를 기반으로 왼쪽위->오른쪽 아래 대각선의 빙고 확인 코드를 작성하면 다음과 같다.
for(int i=0; i<5; i++) {
if(arr[i][i]==0) {// 왼쪽 위->오른쪽 아래 1칸이 색칠되 있는 경우
colorCnt++;// 색칠된 카운트 증가
}
}
if(colorCnt==5) {// 색칠된 카운트=대각선 칸 갯수
bingoCnt++;// 빙고
}
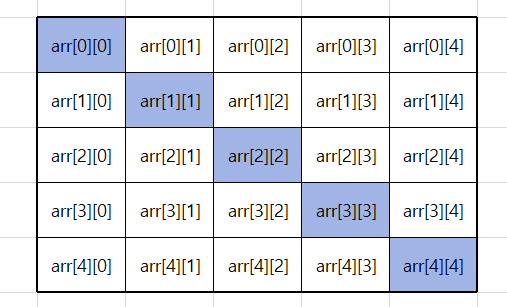
colorCnt=0;// 색칠된 부분 카운트 초기화다음으로 오른쪽 위->왼쪽 아래 부분의 빙고를 배열의 위치로 보면 다음과 같다.
배열의 위치를 유심히 살펴보면 arr[0][4]부터 arr[4][0]까지 배열의 가로의 위치 감소하고, 세로의 위치가 증가하는 부분에 색칠이 칠해진 것을 볼 수 있다.
이를 기반으로 왼쪽위->오른쪽 아래 대각선의 빙고 확인 코드를 작성하면 다음과 같다.
j=4;
for(int i=0; i<5; i++) {
if(arr[i][j]==0) {// 오른쪽 위->왼쪽 아래 1칸이 색칠되 있는 경우
colorCnt++;// 색칠된 카운트 증가
}
j--;
}
if(colorCnt==5) {// 색칠된 카운트=대각선 칸 갯수
bingoCnt++;// 빙고
}
colorCnt=0;// 색칠된 부분 카운트 초기화이러한 내용들을 기반으로 빙고판을 만들어 빙고 갯수를 구하는 코드를 작성하면 다음과 같다.
빙고판:
code
public class Bingo {
public static void main(String[] args) {
int i, j;
int colorCnt=0, bingoCnt=0;
int arr[][]= {
{0, 2, 3, 4, 0},
{0, 0, 0, 0, 10},
{0, 12, 0, 0, 15},
{0, 0, 18, 0, 20},
{0, 22, 0, 24, 0}
};// 빙고판
/*가로*/
for(i=0; i<5; i++) {
for(j=0; j<5; j++) {
if(arr[i][j]==0) {
colorCnt++;
}
}
if(colorCnt==5) {
bingoCnt++;
}
colorCnt=0;// 색칠된 부분 카운트 초기화
}
/*세로*/
for(i=0; i<5; i++) {
for(j=0; j<5; j++) {
if(arr[j][i]==0) {
colorCnt++;
}
}
if(colorCnt==5) {
bingoCnt++;
}
colorCnt=0;// 색칠된 부분 카운트 초기화
}
/*왼쪽 위->오른족 아래*/
for(i=0; i<5; i++) {
if(arr[i][i]==0) {
colorCnt++;
}
}
if(colorCnt==5) {
bingoCnt++;
}
colorCnt=0;// 색칠된 부분 카운트 초기화
/*오른쪽 위->왼쪽 아래*/
j=4;
for(i=0; i<5; i++) {
if(arr[i][j]==0) {
colorCnt++;
}
j--;
}
if(colorCnt==5) {
bingoCnt++;
}
colorCnt=0;// 색칠된 부분 카운트 초기화
System.out.println("bingo: "+bingoCnt);
}
}output
bingo: 33.2 달팽이
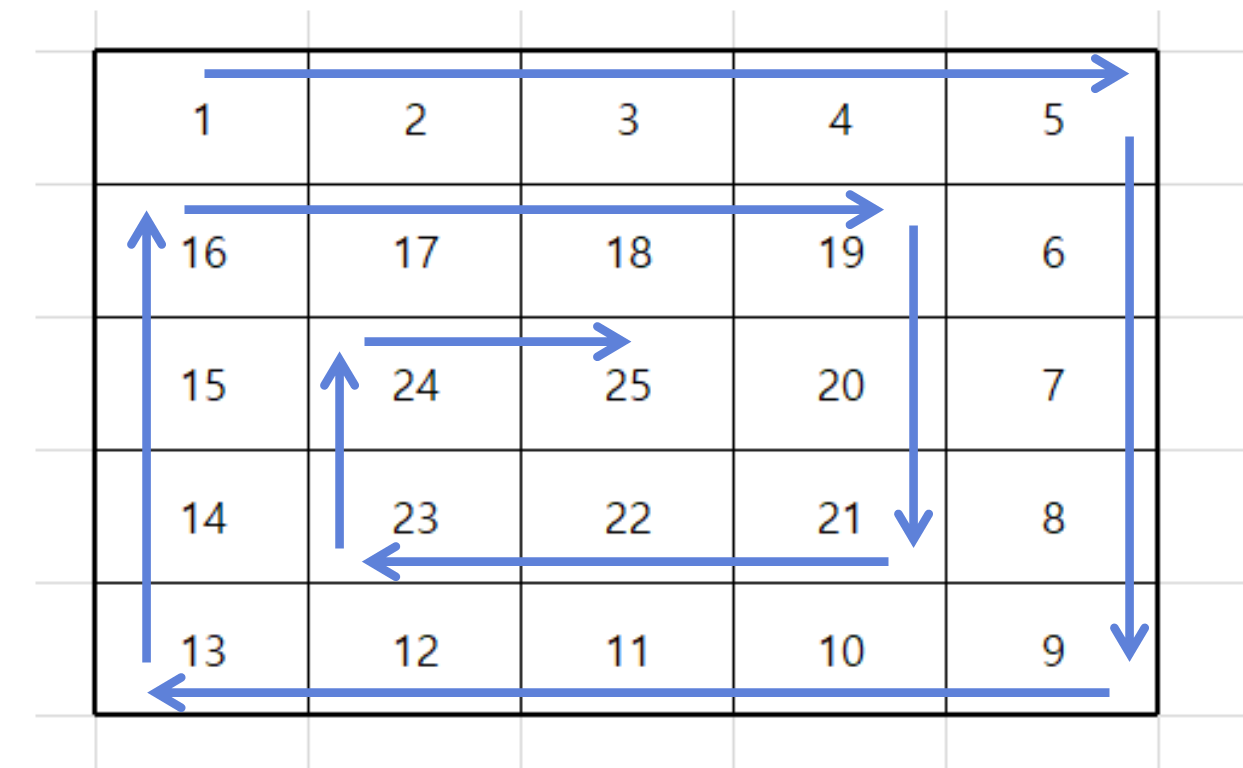
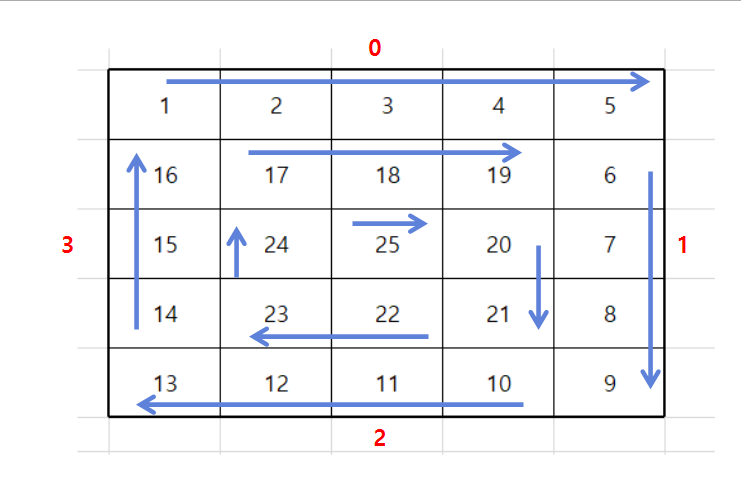
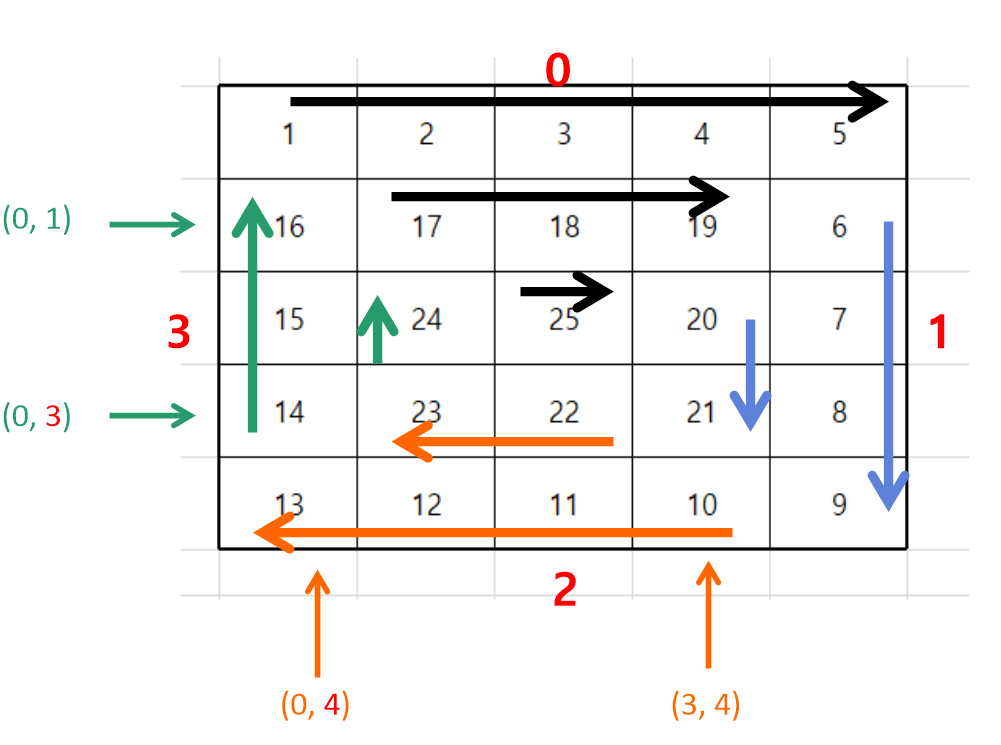
달팽이는 아래 그림과 같이 2차원 배열에서 숫자가 달팽이 모양처럼 배치된 경우이다.
달팽이 문제를 푸는 방법은 다음과 같다.
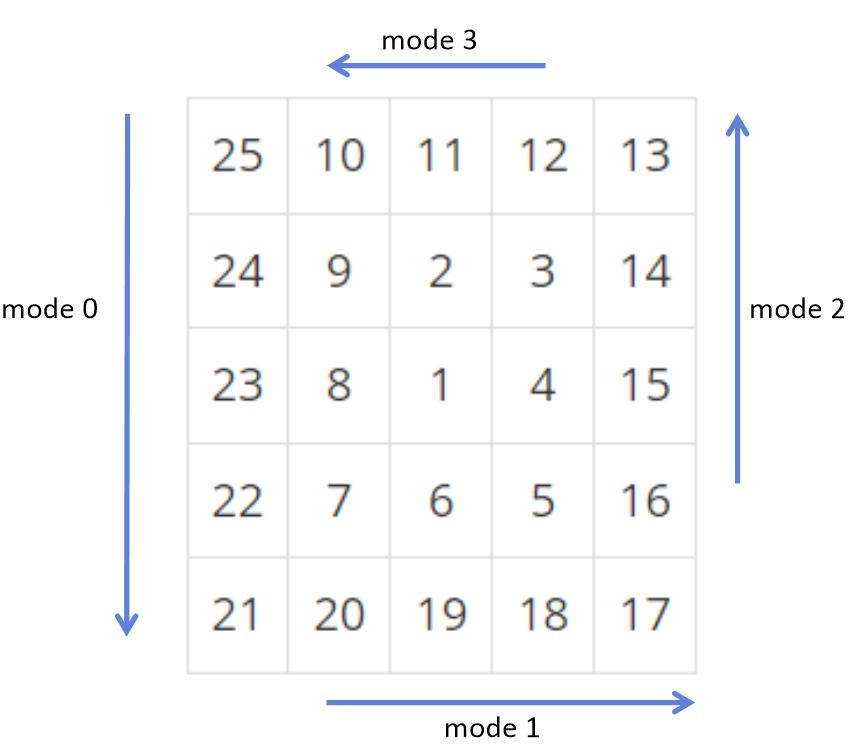
먼저 달팽이를 보면 오른쪽->왼쪽, 위->아래, 왼쪽->오른쪽, 아래->위 이렇게 4가지의 방향이 반복되는 것을 알 수 있다.
이때, 각 방향을 mode라고 하고 mode 0 ~ mode 3으로 나타내면 다음과 같다.
또한, mode가 바뀔 때 마다 아래 그림과 같이 숫자의 시작, 종료 위치가 바뀌는 것을 알 수 있다.
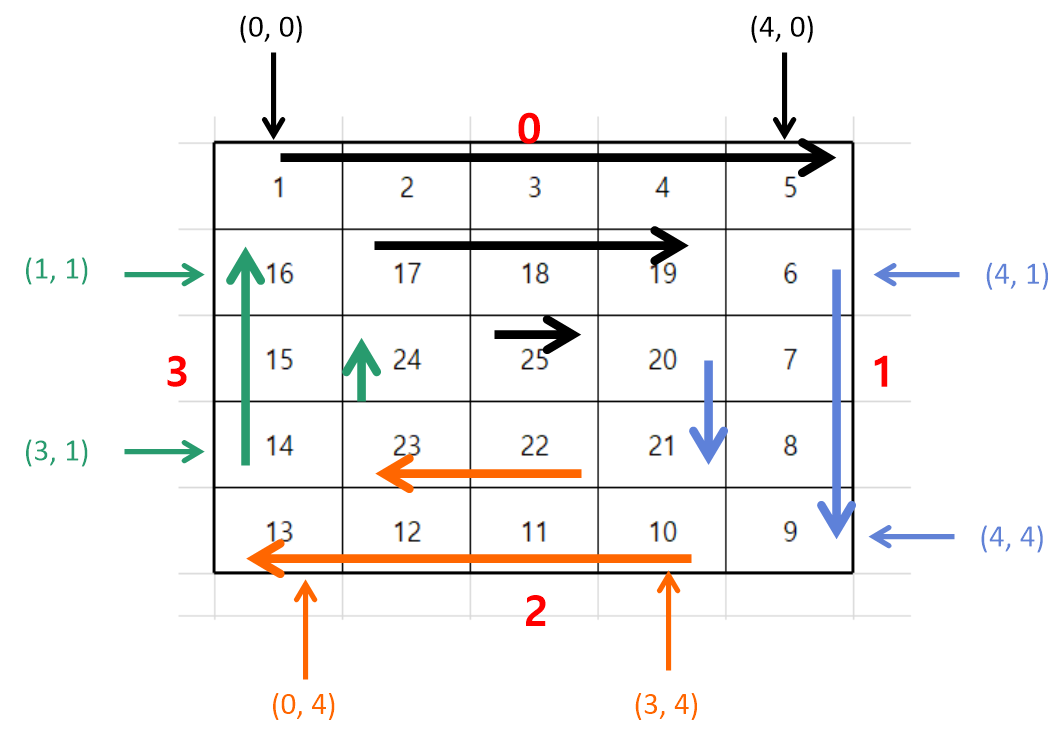
먼저, 최솟값은0, 최댓값은 배열의 y축 길이-1로 지정하고, 각 mode별로 최대/최소값의 변화를 보면 다음과 같다.
-
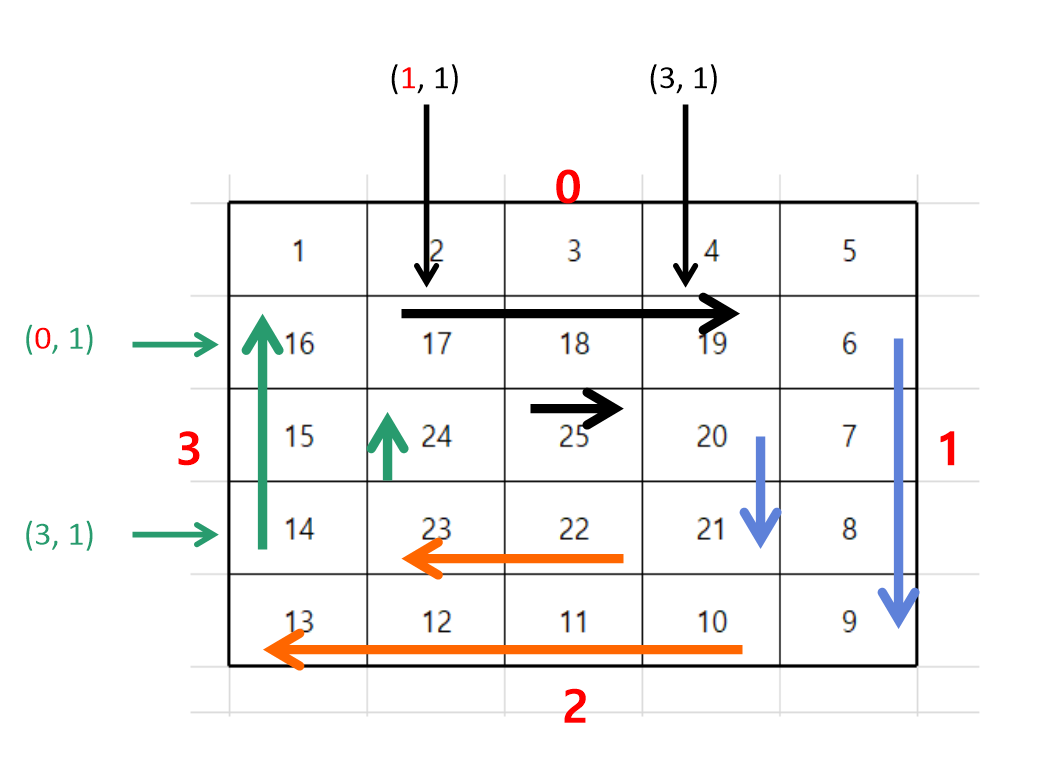
mode 1
mode 1에서는 아래 그림과 같이 y축이 1부터 시작을 하면서 y축의 최소값이 1 증가한다.
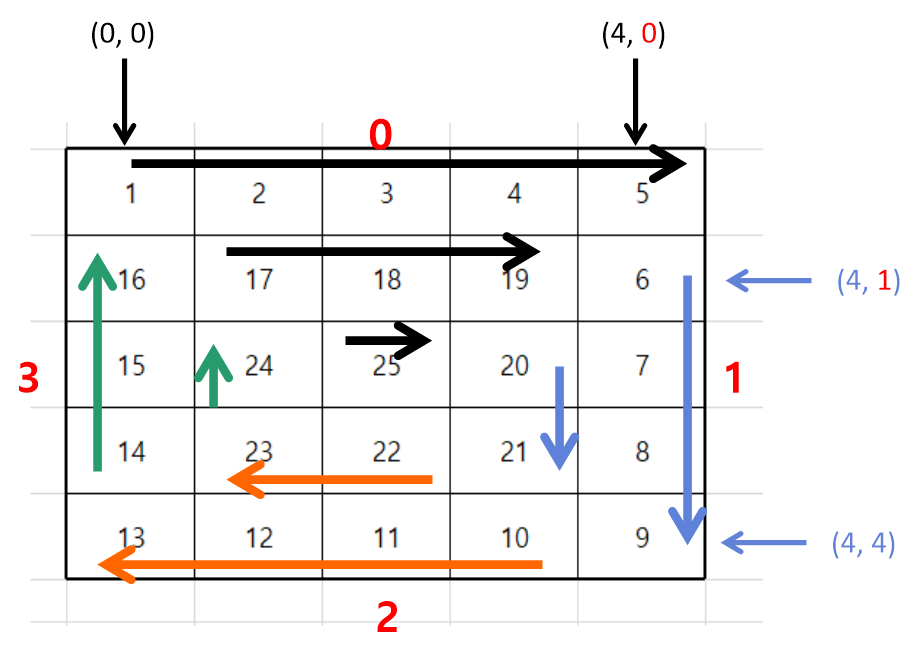
뿐만 아니라,mode 1에서는 y축이 1씩 증가하면서 숫자를 저장하는 규칙이 있다.
또한,mode 1의 시작점은 x축은 최댓값(4), y축은 최솟값(1) 이다. -
mode 2
mode 2에서는 아래 그림과 같이 x축이 3부터 시작을 하면서 의 최댓값이 1 감소한다.
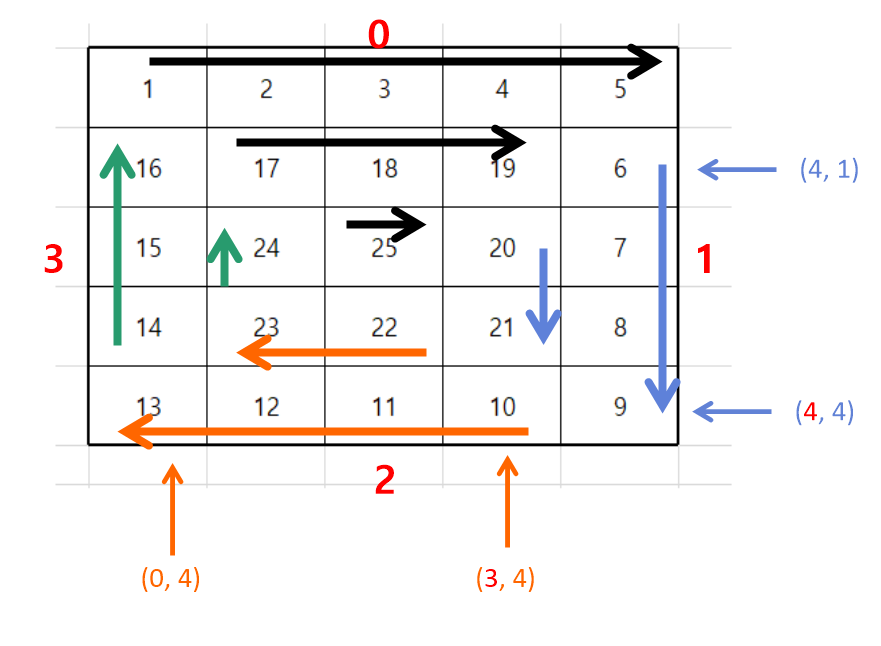
뿐만 아니라, mode 2에서는 x축이 1씩 감소하면서 숫자를 저장하는 규칙이 있다.
또한, mode 2의 시작점은 x축은 최댓값(3), y축은 최댓값(3) 이다.
mode 3
mode 3에서는 아래 그림과 같이 y축이 3부터 시작을 하면서 의 최소값이 1 증가한다.
뿐만 아니라, mode 3에서는 y축이 1씩 감소하면서 숫자를 저장하는 규칙이 있다.
또한, mode 3의 시작점은 x축은 최댓값(0), y축은 최댓값(3) 이다.
mode 0
mode 0에서는 아래 그림과 같이 x축의 최소값이 1 증가한다.
뿐만 아니라,mode 0에서는 x축이 1씩 증가하면서 숫자를 저장하는 규칙이 있다.
또한,mode 0의 시작점은 x축은 최솟값(1), y축은 최솟값(1) 이다.
이와같이 달팽이 문제는 (x, y)의 최대값, 최솟값을 증감시켜 모드별로 숫자를 저장하는 폭을 조절하는 방식으로 작성할 수 있다.
지금까지 알아본 규칙들을 이용해 코드를 작성하면 다음과 같다.
public class Array {
public static void main(String[] args) {
int arr[][]=new int[5][5];
int minX, maxX, minY, maxY;// 최대/최소 위치
int posX, posY;// 시작위치
int mode=0, incX=1, incY=0;// 모드, x/y 증감
int num=1;
/*시작 위치 설정*/
posX=0;
posY=0;
/*범위 설정*/
minX=0;
minY=0;
maxX=4;
maxY=4;
while( num<25 ) {// 종료조건 설정
while( (posX<=maxX && posX>=minX) && (posY<=maxY && posY>=minY) ) {
arr[posY][posX]=num;
posX+=incX;
posY+=incY;
num++;
}
mode++;
mode%=4;
switch(mode) {// 모드
case 0:
incX=1;
incY=0;
minX++;
posX=minX;
posY=minY;
break;
case 1:
incX=0;
incY=1;
minY++;
posX=maxX;
posY=minY;
break;
case 2:
incX=-1;
incY=0;
maxX--;
posX=maxX;
posY=maxY;
break;
case 3:
incX=0;
incY=-1;
maxY--;
posX=minX;
posY=maxY;
break;
default:
break;
}
}
for(int i=0; i<5; i++) {
for(int j: arr[i]) {
System.out.print(j +"\t");
}
System.out.println();
}
}
}output
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9 4. 실습
Q1. 2차원 배열의 합(백준 2167)
문제
2차원 배열이 주어졌을 때 (i, j) 위치부터 (x, y) 위치까지에 저장되어 있는 수들의 합을 구하는 프로그램을 작성하시오. 배열의 (i, j) 위치는 i행 j열을 나타낸다.
입력
첫째 줄에 배열의 크기 N, M(1 ≤ N, M ≤ 300)이 주어진다. 다음 N개의 줄에는 M개의 정수로 배열이 주어진다. 배열에 포함되어 있는 수는 절댓값이 10,000보다 작거나 같은 정수이다. 그 다음 줄에는 합을 구할 부분의 개수 K(1 ≤ K ≤ 10,000)가 주어진다. 다음 K개의 줄에는 네 개의 정수로 i, j, x, y가 주어진다(1 ≤ i ≤ x ≤ N, 1 ≤ j ≤ y ≤ M).
출력
K개의 줄에 순서대로 배열의 합을 출력한다. 배열의 합은 2^31-1보다 작거나 같다.
예제입력
2 3
1 2 4
8 16 32
3
1 1 2 3
1 2 1 2
1 3 2 3예제출력
63
2
36Q2. 색종이(백준 2563)
가로, 세로의 크기가 각각 100인 정사각형 모양의 흰색 도화지가 있다. 이 도화지 위에 가로, 세로의 크기가 각각 10인 정사각형 모양의 검은색 색종이를 색종이의 변과 도화지의 변이 평행하도록 붙인다. 이러한 방식으로 색종이를 한 장 또는 여러 장 붙인 후 색종이가 붙은 검은 영역의 넓이를 구하는 프로그램을 작성하시오.
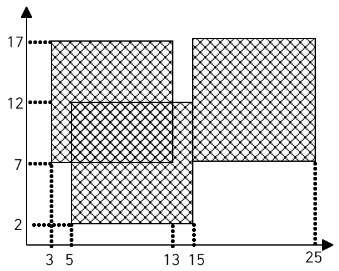
예를 들어 흰색 도화지 위에 세 장의 검은색 색종이를 그림과 같은 모양으로 붙였다면 검은색 영역의 넓이는 260이 된다.
입력
첫째 줄에 색종이의 수가 주어진다. 이어 둘째 줄부터 한 줄에 하나씩 색종이를 붙인 위치가 주어진다. 색종이를 붙인 위치는 두 개의 자연수로 주어지는데 첫 번째 자연수는 색종이의 왼쪽 변과 도화지의 왼쪽 변 사이의 거리이고, 두 번째 자연수는 색종이의 아래쪽 변과 도화지의 아래쪽 변 사이의 거리이다. 색종이의 수는 100 이하이며, 색종이가 도화지 밖으로 나가는 경우는 없다
출력
첫째 줄에 색종이가 붙은 검은 영역의 넓이를 출력한다.
예제입력
3
3 7
15 7
5 2예제출력
260Q3 빙고(백준 2578)
빙고 게임은 다음과 같은 방식으로 이루어진다.
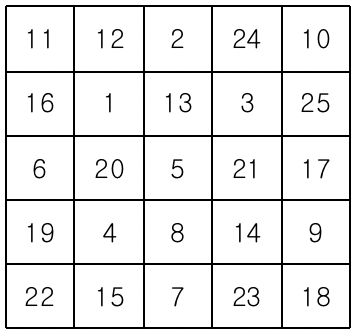
먼저 아래와 같이 25개의 칸으로 이루어진 빙고판에 1부터 25까지 자연수를 한 칸에 하나씩 쓴다
다음은 사회자가 부르는 수를 차례로 지워나간다. 예를 들어 5, 10, 7이 불렸다면 이 세 수를 지운 뒤 빙고판의 모습은 다음과 같다.
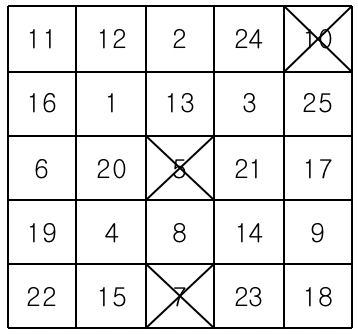
차례로 수를 지워가다가 같은 가로줄, 세로줄 또는 대각선 위에 있는 5개의 모든 수가 지워지는 경우 그 줄에 선을 긋는다.
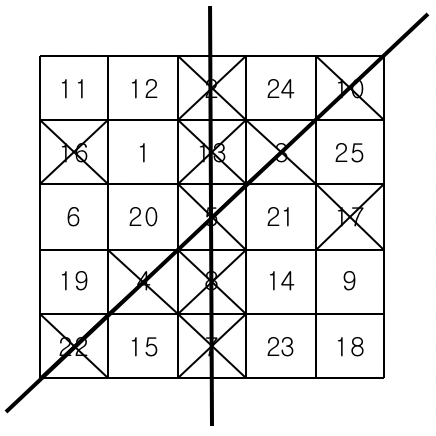
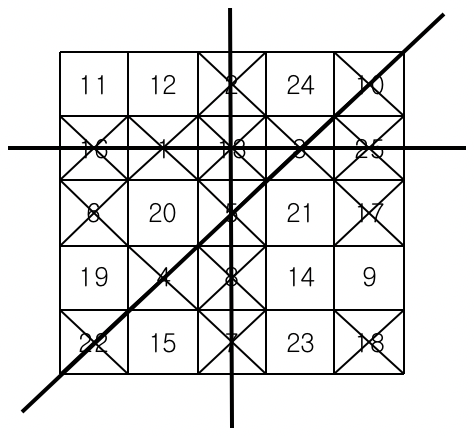
이러한 선이 세 개 이상 그어지는 순간 "빙고"라고 외치는데, 가장 먼저 외치는 사람이 게임의 승자가 된다.
철수는 친구들과 빙고 게임을 하고 있다. 철수가 빙고판에 쓴 수들과 사회자가 부르는 수의 순서가 주어질 때, 사회자가 몇 번째 수를 부른 후 철수가 "빙고"를 외치게 되는지를 출력하는 프로그램을 작성하시오.
입력
첫째 줄부터 다섯째 줄까지 빙고판에 쓰여진 수가 가장 위 가로줄부터 차례대로 한 줄에 다섯 개씩 빈 칸을 사이에 두고 주어진다. 여섯째 줄부터 열째 줄까지 사회자가 부르는 수가 차례대로 한 줄에 다섯 개씩 빈 칸을 사이에 두고 주어진다. 빙고판에 쓰여진 수와 사회자가 부르는 수는 각각 1부터 25까지의 수가 한 번씩 사용된다.
출력
첫째 줄에 사회자가 몇 번째 수를 부른 후 철수가 "빙고"를 외치게 되는지 출력한다.
예제입력
11 12 2 24 10
16 1 13 3 25
6 20 5 21 17
19 4 8 14 9
22 15 7 23 18
5 10 7 16 2
4 22 8 17 13
3 18 1 6 25
12 19 23 14 21
11 24 9 20 15예제출력
15Q4. 달팽이(백준 1913)
홀수인 자연수 N이 주어지면, 다음과 같이 1부터 N2까지의 자연수를 달팽이 모양으로 N×N의 표에 채울 수 있다.
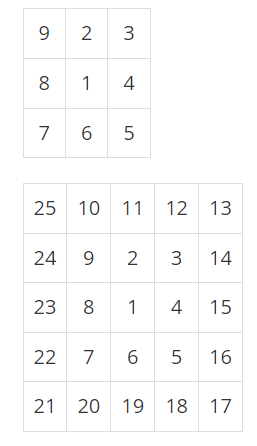
N이 주어졌을 때, 이러한 표를 출력하는 프로그램을 작성하시오. 또한 N2 이하의 자연수가 하나 주어졌을 때, 그 좌표도 함께 출력하시오. 예를 들어 N=5인 경우 6의 좌표는 (4,3)이다.
입력
첫째 줄에 홀수인 자연수 N(3 ≤ N ≤ 999)이 주어진다. 둘째 줄에는 위치를 찾고자 하는 N2 이하의 자연수가 하나 주어진다.
출력
N개의 줄에 걸쳐 표를 출력한다. 각 줄에 N개의 자연수를 한 칸씩 띄어서 출력하면 되며, 자릿수를 맞출 필요가 없다. N+1번째 줄에는 입력받은 자연수의 좌표를 나타내는 두 정수를 한 칸 띄어서 출력한다.
예제입력
7
35예제출력
49 26 27 28 29 30 31
48 25 10 11 12 13 32
47 24 9 2 3 14 33
46 23 8 1 4 15 34
45 22 7 6 5 16 35
44 21 20 19 18 17 36
43 42 41 40 39 38 37
5 7A1
이 문제는 M*N 크기의 배열을 입력받아 배열의 특정 구간의 합을 구하는 문제이다.
아래와 같이 M*N 크기의 배열이 있다 가정하자.
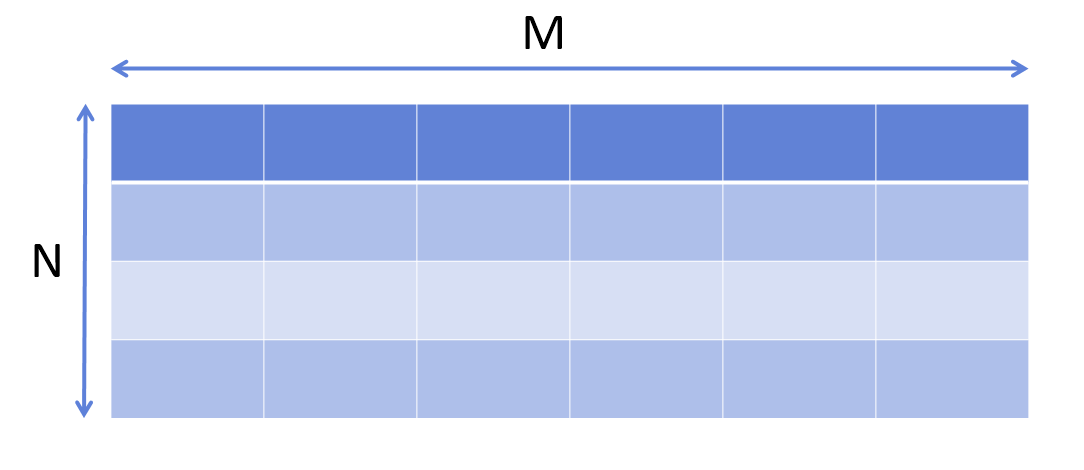
이 M*N배열에서 배열의 (a, b)부터 (x, y)까지의 합을 구하는 방법은 다음과 같다.
먼저, 아래 그림과 같이 합을 구해야 하는 범위를 정한다.
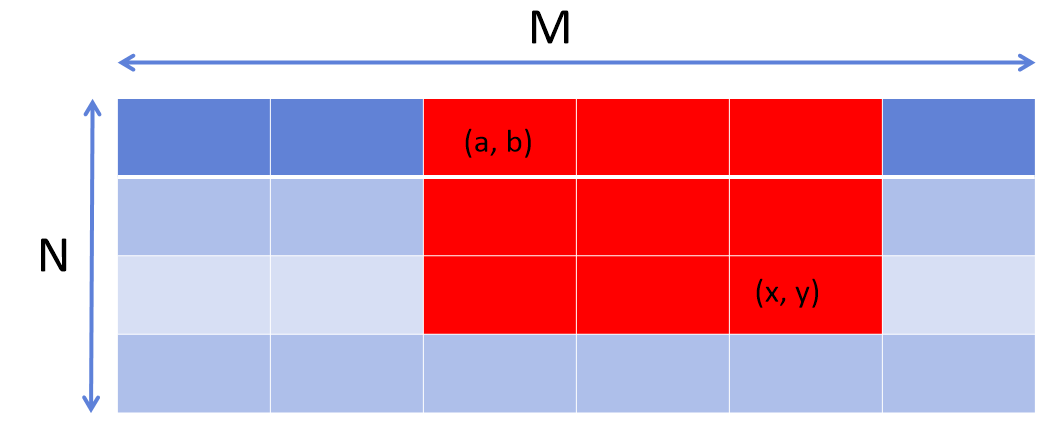
그림을 통해 가로는 a~x, 세로는 b~y까지의 범위를 설정해서 반복문으로 합을 구하면 된다.
a를 startX, x를 endX, b를 startY, y를 endY라고 정의를 하고 코드를 작성하면 다음과 같다.
import java.util.*;
public class Q1 {
public static void main(String[] args) {
int N, M;
int sum;
int i, j, l;
int K;
int startX, startY, endX, endY;
Scanner sc=new Scanner(System.in);
/*배열 크기 입력*/
N=sc.nextInt();
M=sc.nextInt();
int arr[][]=new int[N][M];
/*배열 값 입력*/
for(i=0; i<N; i++) {
for(j=0; j<M; j++) {
arr[i][j]=sc.nextInt();
}
}
K=sc.nextInt();// 합 구하는 갯수 입력
for(i=0; i<K; i++) {
sum=0;
/*시작, 종료위치 입력*/
startY=sc.nextInt()-1;
startX=sc.nextInt()-1;
endY=sc.nextInt();
endX=sc.nextInt();
/*합 구하기*/
for(j=startY; j<endY; j++) {
for(l=startX; l<endX; l++) {
sum+=arr[j][l];
}
}
System.out.println(sum);
}
}
}클래스 이름을 Main으로 변경 후 제출하면 정답임을 확인할 수 있다.
A2
이 문제는 100*100 크기의 도화지 위에 색종이를 붙였을 때의 넓이를 구하는 문제이다.
색종이의 경우 겹쳐질 수 있으며, 색종이가 도화지를 벗어나지는 못한다는 조건이 있다.
이러한 색종이 문제의 경우 100*100 크기의 배열을 선언해 도화지라고 하고, 아래 그림과 같이 색종이 좌표를 기준으로 색종이 크기인 10*10만큼만 1로 색종이가 붙었다는 표시를 하는 방식으로 색종이 영역을 표현할 수 있다.
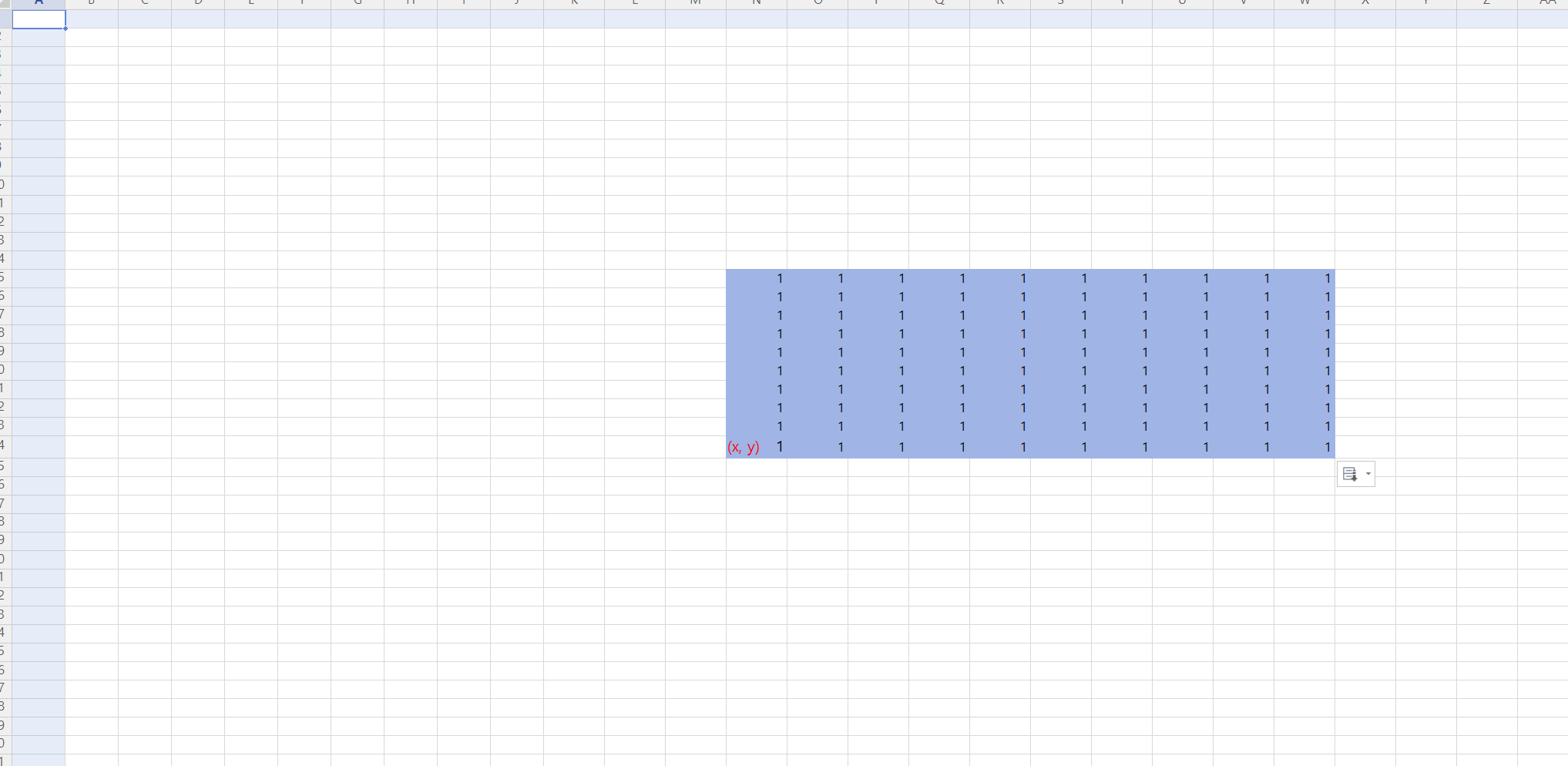
import java.util.*;
public class Q2 {
public static void main(String[] args) {
int arr[][]=new int[100][100];// 도화지 배열
int paperCnt;// 색종이 갯수
int x, y;// 색종이 좌표
int i, j, k;
int area=0;// 색종이 영역 넓이
Scanner sc=new Scanner(System.in);
paperCnt=sc.nextInt();// 색종이 갯수 입력
for(i=0; i<paperCnt; i++) {// 색종이 갯수만큼 반복
/*색종이 좌표 입력*/
x=sc.nextInt();
y=sc.nextInt();
/*색종이 부착*/
for(j=x; j<x+10; j++) {
for(k=y; k<y+10; k++) {
arr[j][k]=1;
}
}
}
/*색종이 면적 계산*/
for(i=0; i<arr.length; i++) {
for(j=0; j<arr[i].length; j++) {
area+=arr[i][j];
}
}
System.out.println(area);
}
}A3
이번 문제는 빙고 문제로, 주어진 빙고판에서 차례대로 숫자를 부를때 3빙고가 될때의 횟수를 출력하는 문제이다.
빙고의 경우 위에서 설명한 알고리즘을 그대로 사용하면 되며, while반복문으로 3빙고가 될 때 까지 반복을 하면서 카운트 변수에 값을 늘려주는 방식으로 작성하면 된다.
import java.util.*;
public class Q3 {
public static void main(String[] args) {
int i, j;
int num;
int cnt=0;// 게임 횟수
int colorCnt=0, bingoCnt=0;
int arr[][]= new int[5][5];
Scanner sc=new Scanner(System.in);
/*빙고판 입력*/
for(i=0; i<5; i++) {
for(j=0; j<5; j++) {
arr[i][j]=sc.nextInt();
}
}
while(bingoCnt<3) {
bingoCnt=0;// 빙고 초기화(안해주면 빙고가 누적됨)
num=sc.nextInt();// 숫자 받아오기
numFinder:
/*빙고판에서 숫차 찾기*/
for(i=0; i<5; i++) {
for(j=0; j<5; j++) {
if(arr[i][j]==num) {
arr[i][j]=0;
break numFinder;
}
}
}
/*가로*/
for(i=0; i<5; i++) {
for(j=0; j<5; j++) {
if(arr[i][j]==0) {
colorCnt++;
}
}
if(colorCnt==5) {
bingoCnt++;
}
colorCnt=0;// 색칠된 부분 카운트 초기화
}
/*세로*/
for(i=0; i<5; i++) {
for(j=0; j<5; j++) {
if(arr[j][i]==0) {
colorCnt++;
}
}
if(colorCnt==5) {
bingoCnt++;
}
colorCnt=0;// 색칠된 부분 카운트 초기화
}
/*왼쪽 위->오른족 아래*/
for(i=0; i<5; i++) {
if(arr[i][i]==0) {
colorCnt++;
}
}
if(colorCnt==5) {
bingoCnt++;
}
colorCnt=0;// 색칠된 부분 카운트 초기화
/*오른쪽 위->왼쪽 아래*/
j=4;
for(i=0; i<5; i++) {
if(arr[i][j]==0) {
colorCnt++;
}
j--;
}
if(colorCnt==5) {
bingoCnt++;
}
colorCnt=0;// 색칠된 부분 카운트 초기화
cnt++;
}
System.out.println(cnt);
}
}A4
이번 문제는 달팽이 문제로, mode 0 ~ mode 3까지의 규칙을 이용해 문제를 풀 수 있다.
숫자는 N*N 부터 시작해 1씩 감소하는 방식이며, 각 mode별로 특징은 다음과 같다.
-
mode 0
y좌표 증가, y최솟값 증가
시작좌표: (x 최솟값, y 최솟값) -
mode 1
x좌표 증가, x최솟값 증가
시작좌표: (x 최솟값, y 최댓값) -
mode 2
y좌표 감소, y최댓값 감소
시작좌표: (x 최댯값, y 최댓값) -
mode 3
x좌표 감소, x최댓값 감소
시작좌표: (x 최댓값, y 최솟값)
import java.util.*;
public class Q4 {
public static void main(String[] args) {
int minX, maxX, minY, maxY;
int posX, posY;
int mode=0, incX=0, incY=1;
StringBuilder sb = new StringBuilder();
Scanner sc=new Scanner(System.in);
int size=sc.nextInt();
int find=sc.nextInt();
int arr[][]=new int[size][size];
int num=size*size;
/*시작 위치 설정*/
posX=0;
posY=0;
/*범위 설정*/
minX=0;
minY=0;
maxX=size-1;
maxY=size-1;
while( num>0 ) {// 종료조건
while( (posX<=maxX && posX>=minX) && (posY<=maxY && posY>=minY) ) {
arr[posY][posX]=num;
posX+=incX;
posY+=incY;
num--;
}
mode++;
mode%=4;
switch(mode) {
case 0:
incX=0;
incY=1;
minY++;
posX=minX;
posY=minY;
break;
case 1:
incX=1;
incY=0;
minX++;
posX=minX;
posY=maxY;
break;
case 2:
incX=0;
incY=-1;
maxY--;
posX=maxX;
posY=maxY;
break;
case 3:
incX=-1;
incY=0;
maxX--;
posX=maxX;
posY=minY;
break;
default:
break;
}
}
for(int i=0; i<size; i++) {
for(int j: arr[i]) {
sb.append(j+" ");
}
sb.append("\n");
}
System.out.print(sb);
for(int i=0; i<size; i++) {
for(int j=0; j<size; j++) {
if(arr[i][j]==find) {
System.out.println( (i+1)+" "+(j+1));
}
}
}
}
}위 주소에서 code를 다운로드 받아 eclipse로 직접 정답 확인이 가능하다.
https://github.com/isaiahIM/java_basic/tree/main/array%202D