AI 추론 관점에서 Quantization 기초 살펴보기

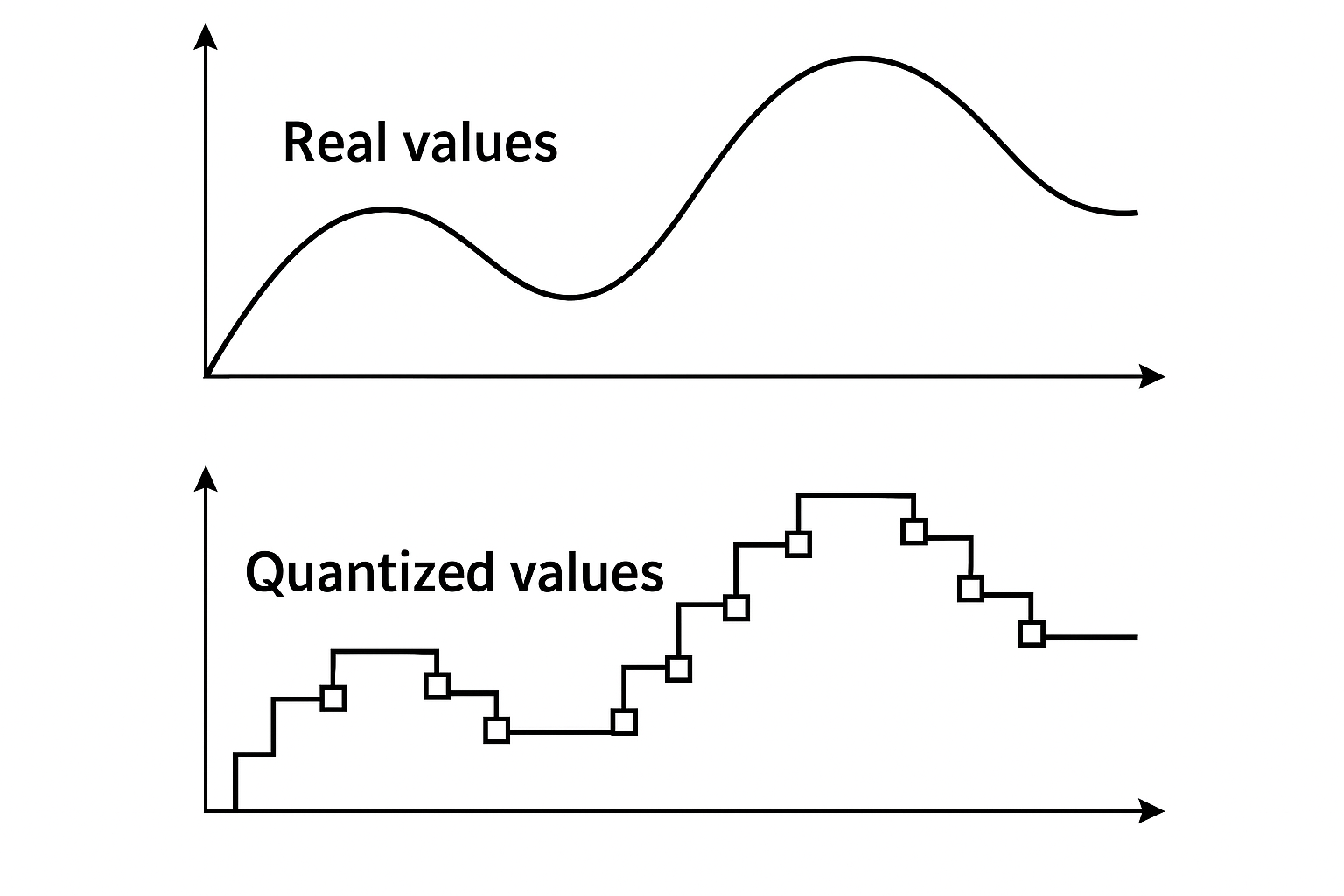
추론(inference) 성능을 높이기 위한 다양한 기법 중, quantization은 현대적인 AI 모델을 실제 서비스에 배포(deploy)할 때 필수적인 기술이 되었습니다.

저는 현재 Intel에서 OpenVINO GPU 백엔드 팀의 테크 리드이자 코드 maintainer(approver)로 일하고 있습니다.
그동안 실무에서 quantization 최적화, 리뷰, 성능 개선을 직접 경험하였고, 이 글에서는 그 관점에서 quantization의 개념과 동작 원리를 정리해보았습니다.

단순히 "float 대신 int를 쓴다"로 이해하기 쉬운 듯 보이지만, 실제로는 scale, zero-point, requantization, compensation 등 실전에서 고려할 점이 많습니다.

또한 quantization은 단순한 커널 수준의 최적화에 그치지 않고, 하드웨어 아키텍처의 연산 유닛, 메모리 대역폭과도 긴밀히 연결된 주제이며, 모델 준비 단계(QAT 또는 Post-Training Optimization), 정확도 평가, 배포 전략 등 딥러닝 모델 라이프사이클 전반에 영향을 미치는 기술입니다.

이 글에서는 quantization의 기본 개념을 먼저 다루고, 이어지는 글에서 static/dynamic quantization, requantization, 성능 trade-off 등 실무적인 주제로 확장해 나갈 예정입니다.

🔍 시리즈 구성

1. AI 추론 관점에서 Quantization 기초 살펴보기 <-- 이번 글

2. AI Inference최적화를 위한 Static Quantization과 Requantization

3. LLM 추론 최적화를 위한 Dynamic Quantization

Quantization이란 무엇인가?

AI영역에서 Quantization (정량화)는 float값을 int 값으로 바꾸는 것을 말한다. 주로 fp16/fp32를 int4/int8으로 변환하게 된다. 무작정 변환하는 것은 아니고, 텐서 안에 있는 실수 값의 최소값과 최대값을 기준으로 정수 범위에 맞게 normalize한다.

예를 들어, 다음과 같은 float 벡터가 있다고 해보자.

fp_data = [0.0, 0.1, 0.2, 0.3]

이 데이터를 uint8 타입으로 quantize 하면 다음과 같이 바뀐다:

Uint8_data = [0, 85, 170, 255], scale = 0.001176

이 정수 값에 scale을 곱하면 원래 float 값 비슷하게 다시 나오는 것이다.
즉, quantization은 데이터의 분포(min/max)를 보고 그걸 우리가 원하는 정수 범위(Int8, Int4 등)에 맞춰 매핑하는 작업인 것이다. 이때 scale이 꼭 필요하고, 몇 개 값을 묶어서 quantize하느냐(예: per-tensor, per-channel, group-wise)에 따라 scale도 달라지고, 정량화된 결과도 달라진다.

왜 Quantization이 중요할까?

Quantization이 중요한 이유는 낮은 정밀도로 AI 연산을 수행하는 것이 높은 정밀도로 연산하는 것보다 훨씬 더 효율적이기 때문이다.

여기서 말하는 효율성은 다음과 같이 정리할 수 있다:

• 실리콘 면적을 적게 차지하고,
• 전력 소모가 줄어들고,
• 메모리와 저장 공간을 적게 사용하며,
• 연산 속도도 빨라진다.

이렇게 보면 모든 것이 완벽한데, 단점은 없을까?

대표적인 단점은 데이터 손실, 즉 quantization error가 발생한다는 점이다. 정밀도가 높은 형식(fp16, fp32)에 비해 표현 가능한 값의 범위가 제한되기 때문에, 일부 정보는 손실될 수밖에 없다.

그럼에도 불구하고, 대부분의 AI 모델에서는 이런 정량화 오류가 큰 문제가 되지 않는다. AI 모델은 수많은 weight들이 서로 상호작용하면서 동작하기 때문에, 일부 값에 오차가 생기더라도 전체 성능에는 큰 영향을 주지 않는 경우가 많기 때문이다. 즉, 모델 자체가 어느 정도 오류에 robust하게 설계되어 있기 때문이다.

Weight 정량화 vs. activation 정량화

딥러닝 모델에서 주로 다뤄지는 데이터는 크게 보면 가중치(weight)와 입력값(activation)이다. 이 둘을 가지고 여러 연산자(operator)가 구현되지만, 여기서는 대표적인 연산인 행렬곱(matrix multiplication, 또는 fully connected) 형태로 설명해보겠다.

Output = activation * weight

이 연산에서 activation과 weight 중 어떤 쪽을 quantize 하느냐에 따라, 성능과 메모리 특성이 크게 달라진다.

• Activation과 weight를 모두 정량화: 가장 이상적인 경우다. 이렇게 하면 곱셈 연산을 int8로 수행할 수 있어서, 앞에서 말한 효율성, 전력, 수행시간 등 모든 이점을 누릴 수 있다. 다만 둘 다 정량화되기 때문에 quantization error가 커지고, 네트워크 정확도에 영향을 줄 가능성이 높다. CNN 기반 컴퓨터 비전 모델에서는 이 방식이 잘 작동했다.

• Weight만 정량화: 이 경우 activation은 fp16이나 fp32를 그대로 사용하고, weight만 int4/int8로 바꾼다. 이렇게 하면 곱셈 연산은 여전히 float 기반으로 돌아가므로, 연산 자체에서의 속도 이득은 없다. 대신 weight 용량이 줄어들기 때문에 저장 공간이 줄고, 메모리 사용량도 감소한다. 특히 weight 로딩 때문에 IO-bound되는 상황에서는 이 방식이 오히려 성능 향상으로 이어질 수 있다. (예를들면 LLM 2nd token)

• Activation만 정량화: 이 경우는 현실적으로 거의 사용되지 않는다. 연산 성능이나 IO 측면에서 얻는 이득이 거의 없기 때문이다. weight가 float인 이상, 곱셈 연산은 여전히 float로 이뤄지고, activation을 정량화한다고 해서 메모리 이득도 별로 없다.

스태틱 정량화와 다이나믹 정량화

activation이나 weight을 정량화하려면 scale 값을 알아야 하는데, 그걸 어떻게 결정하느냐에 따라 접근 방식이 달라진다.

weight은 학습이 끝나면 값이 고정되기 때문에, 정량화가 비교적 단순하다. 그냥 값들을 보고 min/max를 구해서 scale을 정하면 된다. 물론 정량화를 고려한 추가 학습도 가능하지만, 이 글에서는 다루지 않겠다.

반면 activation의 scale을 구하는 방법은 두 가지로 나뉜다: 스태틱 방식과 다이나믹 방식이다.

• Static quantization: 흔히 PTQ(Post-training quantization)라고 부른다. 여러 입력 데이터를 미리 넣어보고 각 레이어의 activation 분포를 수집해서 정량화하는 방식이다. 예를 들어 얼굴 인식 네트워크라면, 다양한 얼굴 이미지를 넣어 activation이 어느 정도 범위에서 움직이는지 본다. 이 과정을 calibration이라고 하고, 여기서 얻은 min/max를 가지고 scale을 정하게 된다.
• Dynamic quantization: 트랜스포머 같은 네트워크에서는 입력 종류에 따라 activation 분포가 크게 달라져서 스태틱 방식이 잘 동작하지 않는다. 이런 경우에, 네트워크가 실제로 실행될 때 각 레이어의 min/max를 실시간으로 구해서 scale을 정하는 방식이 Dynamic quantization이다. 이렇게 하면 quantization error는 줄일 수 있지만, 매번 분포를 계산해야 하므로 성능은 떨어질 수밖에 없다.

이 글에서는 스태틱 방식에 초점을 맞춰 설명할 예정이다.

Quantization의 기본적인 공식

정량화를 이해하는 데에는 내적(inner product) 연산을 기준으로 보는 게 가장 직관적이다. 내적은 결국 행렬곱의 기본 단위이기 때문이다.

실수 연산에서의 내적은 이렇게 표현된다. 여기서 xᵢ와 wᵢ는 모두 부동소수점 수이기 때문에, 연산 자체가 float로 수행되고 성능이 떨어진다.

(1) $y = \sum_{i} x_i * w_i$

$x$는 입력 벡터, $w$는 weight, $y$는 결과 값이다.

여기서 아래 공식과 같이 실수 값 $x_i$를 다음과 같이 정수값($\tilde{x}_i$)과 실수 스케일($s_x$)의 곱으로 표현할 수 있고(2), 또 다시 반대로 정수값을 실수 값으로 변환할 수도 있다.(3)

(2) $\tilde{x}_i=round(x_i/s_x)$
(3) $x_i=\tilde{x}_i*s_x$

Weight에 대해서도 마찬가지 변환을 적용하면, (1)의 내적 연산은 이렇게 바뀐다.

(4) $y=\sum_{i}(\tilde{x}_i*s_x)*(\tilde{w}_i*s_w)$

이때, scale 값이 인덱스 i와 무관하다면 (즉, quantization이 벡터 단위로 이뤄진다면), scale을 시그마 밖으로 빼낼 수 있다. CNN에서는 보통 이렇게 quantization이 이뤄진다.

(5) $y=s_x * s_w * \sum_{i}(\tilde{x}_i*\tilde{w}_i)$

이 공식의 핵심은, 실수 계산은 scale만으로 처리하고, 실제 곱셈은 정수값으로 수행할 수 있다는 점이다.
이 구조 덕분에 실제 연산에서는 int8 곱셈과 int32 누산으로 빠르게 계산이 가능해진다.

마치며

Quantization은 CNN뿐만 아니라 최근 주목받는 LLM에서도 중요한 성능 향상 기술로 자리잡고 있다. 단순한 연산 최적화를 넘어서, 모델의 전체적인 효율성과 시스템 운영 비용(TCO; Total Cost of Ownership)까지 영향을 미치는 전략적 요소이기 때문이다. 이 글에서는 quantization의 핵심 개념과 정량화 방식 간의 차이점, 그리고 실무 적용 시 고려해야 할 기술적 포인트들을 정리해보았다.

Dynamic quantization에 대한 좀 더 구체적인 이야기는 아래 링크에서 이어서 볼 수 있다: LLM 추론 최적화를 위한 Dynamic Quantization

참고자료

• HuggingFace quantization 문서
• LLM 추론 최적화를 위한 Dynamic Quantization
• AI 모델의 IO-bound vs Compute-bound 개념과 분석 방법