[BOJ] 10830 행렬 제곱 바로가기
📍 문제
크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
📍 입력
첫째 줄에 행렬의 크기 N과 B가 주어진다. (2 ≤ N ≤ 5, 1 ≤ B ≤ 100,000,000,000)
둘째 줄부터 N개의 줄에 행렬의 각 원소가 주어진다. 행렬의 각 원소는 1,000보다 작거나 같은 자연수 또는 0이다.
📍 출력
첫째 줄부터 N개의 줄에 걸쳐 행렬 A를 B제곱한 결과를 출력한다.
📍 풀이
🧷 풀이 과정
만약 B 의 값이 100,000,000,000 일 경우 행렬 A 를 100,000,000,000 만큼 직접 제곱하는 것은 시간 초과 문제를 절대 해결하지 못한다.
시간 초과 문제를 해결하기 위해서 분할 정복(Divide and Conquer) 알고리즘을 사용해야 한다.
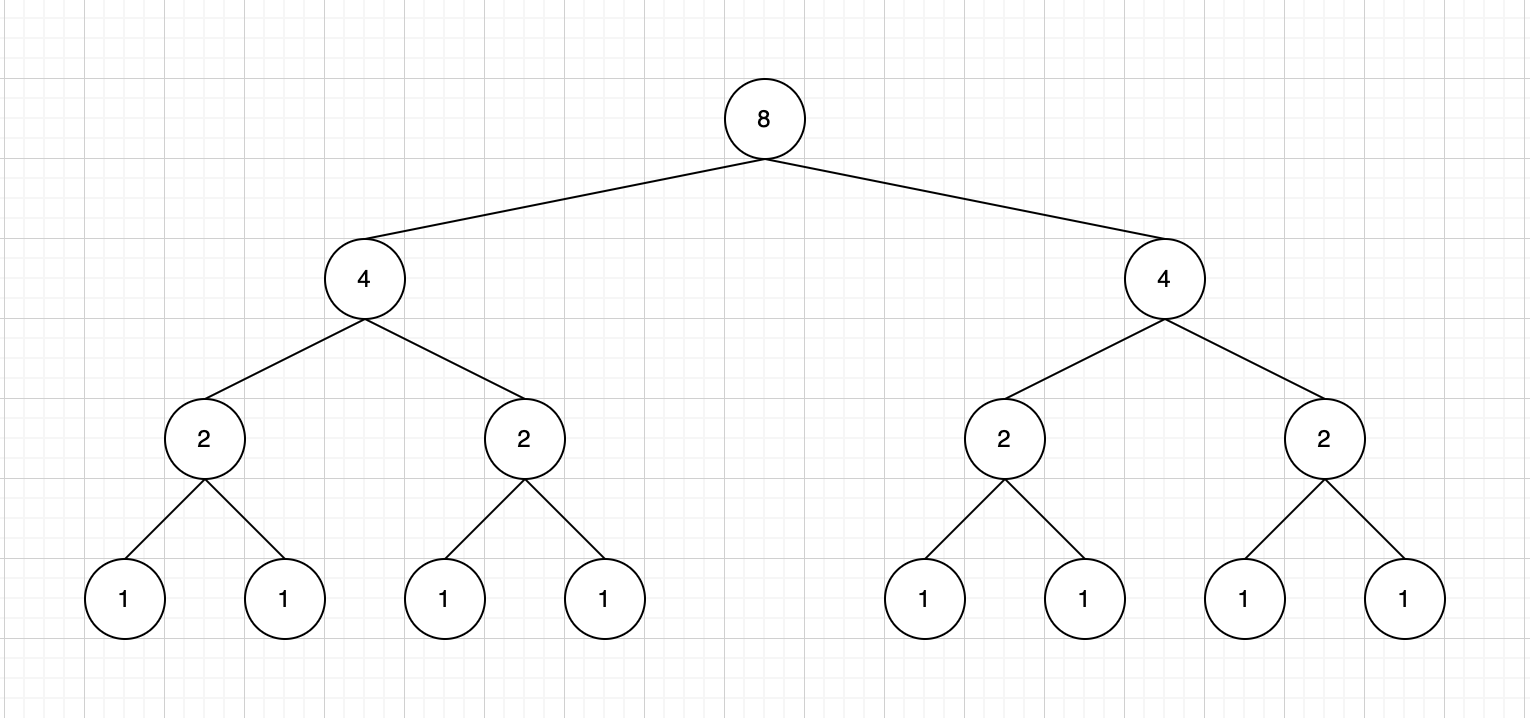
만약 B 의 값이 8 이라면 8 → 4 * 4 → 2 * 2 * 2 * 2 → 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1 로 분할 할 수 있다.
해당 트리의 노드에 적힌 숫자의 의미는 행렬 A 의 제곱 연산의 횟수이다.
만약 노드에 적힌 숫자가 4 라면 행렬 A 의 4제곱이라는 뜻이다.
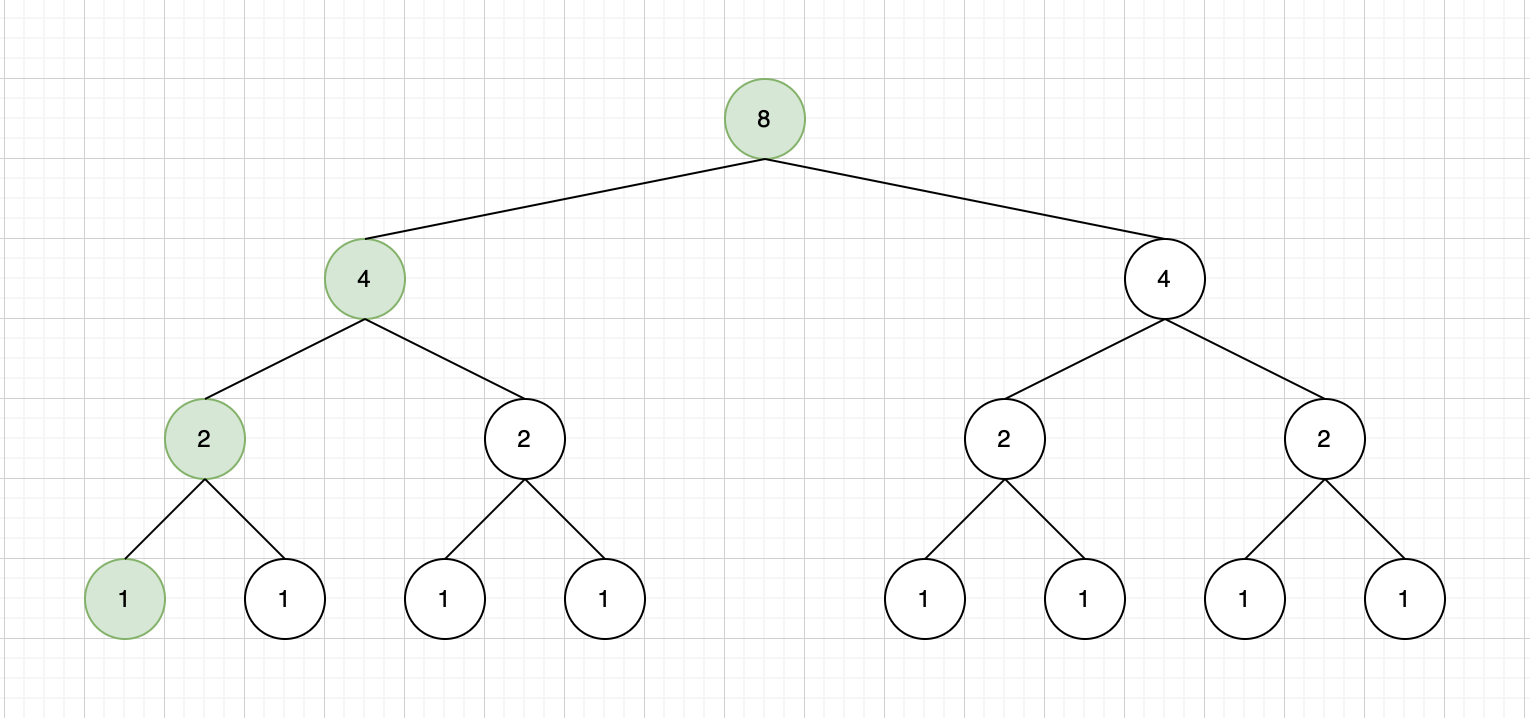
A의 8제곱을 분할 정복을 통해 구하는 과정은 다음과 같다.
- A의 2제곱은 연산(
A * A)을 통해 구한다. - A의 4제곱은 위에서 구한 A의 2제곱을 곱하는(
A^2 * A^2) 연산을 통해 구한다. - A의 8제곱은 위에서 구한 A의 4제곱을 곱하는(
A^4 * A^4) 연산을 통해 구한다.
분할 정복 방식을 통해서 8번의 연산을 3번의 연산으로 줄일 수 있다.
✍ 코드
# BOJ 10830 행렬 제곱
# https://www.acmicpc.net/problem/10830
from sys import stdin
from collections import defaultdict
def solution(N, B, A):
dictionary = defaultdict(list)
dictionary[1] = A
for i in range(N):
for j in range(N):
if A[i][j] == 1000:
A[i][j] = 0
# A행렬 * B행렬
def matrixSquared(A, B):
tmp = [[0] * N for _ in range(N)]
for i in range(N):
for j in range(N):
tmp[j][i] = sum(B[j][k] * A[k][i] for k in range(N)) % 1000
return tmp
# 분할 정복
def divideQunquer(N):
print(N, end=" ")
if N == 1:
return A
else:
return matrixSquared(divideQunquer(N//2), divideQunquer(N//2+N%2))
return divideQunquer(B)
# input
N, B = map(int,stdin.readline().split())
A = [list(map(int,stdin.readline().split())) for _ in range(N)]
# result
result = solution(N, B, A)
for res in result:
print(*res)
