[BOJ] 1516 게임 개발 바로가기
📍 문제
숌 회사에서 이번에 새로운 전략 시뮬레이션 게임 세준 크래프트를 개발하기로 하였다. 핵심적인 부분은 개발이 끝난 상태고, 종족별 균형과 전체 게임 시간 등을 조절하는 부분만 남아 있었다.
게임 플레이에 들어가는 시간은 상황에 따라 다를 수 있기 때문에, 모든 건물을 짓는데 걸리는 최소의 시간을 이용하여 근사하기로 하였다. 물론, 어떤 건물을 짓기 위해서 다른 건물을 먼저 지어야 할 수도 있기 때문에 문제가 단순하지만은 않을 수도 있다. 예를 들면 스타크래프트에서 벙커를 짓기 위해서는 배럭을 먼저 지어야 하기 때문에, 배럭을 먼저 지은 뒤 벙커를 지어야 한다. 여러 개의 건물을 동시에 지을 수 있다.
편의상 자원은 무한히 많이 가지고 있고, 건물을 짓는 명령을 내리기까지는 시간이 걸리지 않는다고 가정하자.
📍 입력
첫째 줄에 건물의 종류 수 N(1 ≤ N ≤ 500)이 주어진다. 다음 N개의 줄에는 각 건물을 짓는데 걸리는 시간과 그 건물을 짓기 위해 먼저 지어져야 하는 건물들의 번호가 주어진다. 건물의 번호는 1부터 N까지로 하고, 각 줄은 -1로 끝난다고 하자. 각 건물을 짓는데 걸리는 시간은 100,000보다 작거나 같은 자연수이다. 모든 건물을 짓는 것이 가능한 입력만 주어진다.
📍 출력
N개의 각 건물이 완성되기까지 걸리는 최소 시간을 출력한다.
📍 풀이
🧷 풀이 과정
위상 정렬 (Topological Sorting) 알고리즘을 이용하여 문제를 해결할 수 있다.
문제에서 주어진 조건 중 중요한 포인트는 여러 개의 건물을 동시에 지을 수 있다. 는 부분이다.
해당 조건은 동시에 건물을 건설하는 것이 가능하므로 건물을 짓기 위해 먼저 지어야 하는 건물 목록(선행 건물) 중 가장 건설 기간이 긴 건물의 건실 시간(max(선행 건물 건실 시간))을 현재 건물의 건설 시간에 더하는 방식으로 문제를 해결할 수 있다.
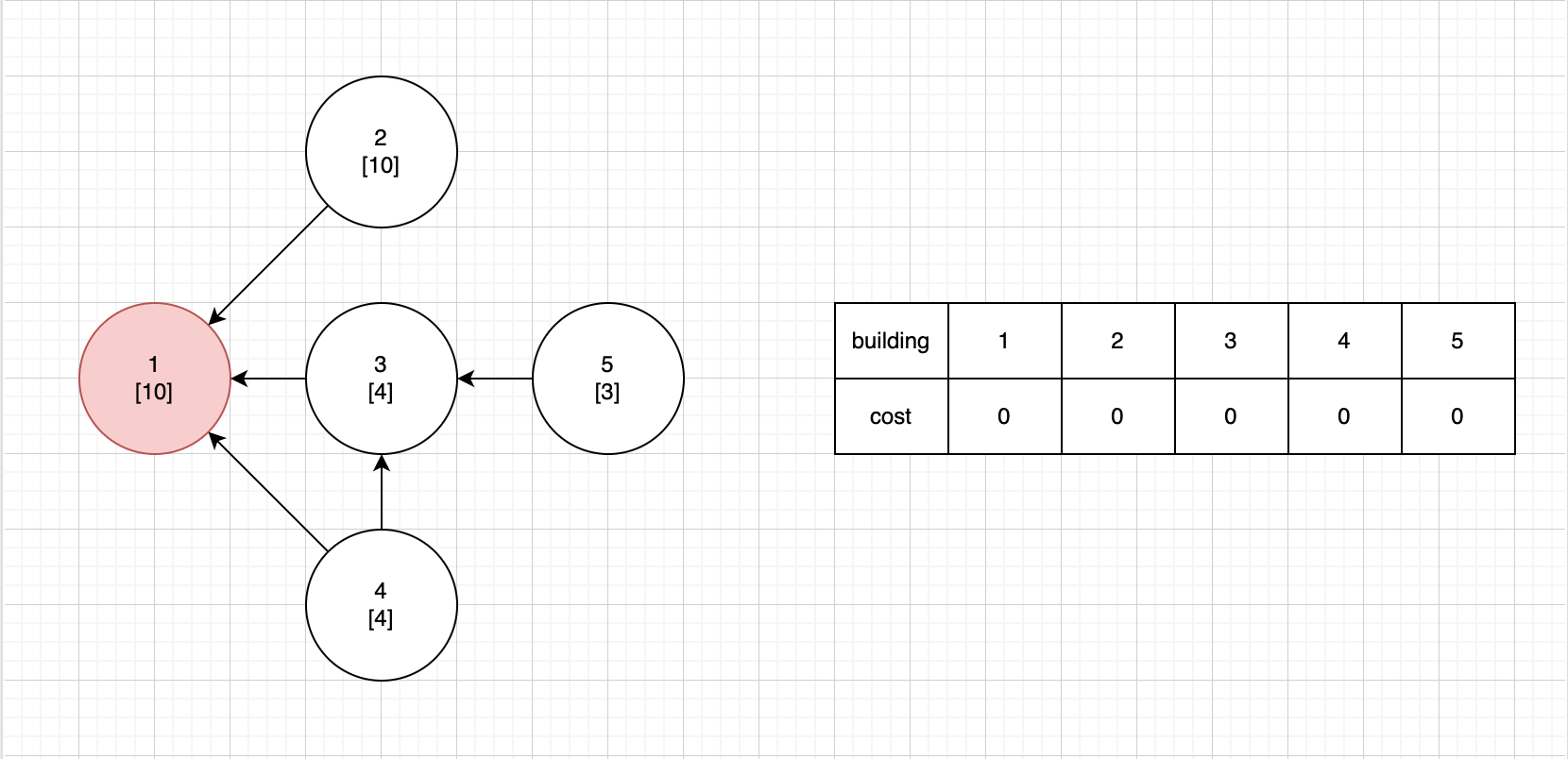
- 1번 건물의 경우 현재 진입 차수가 0 이므로 제거한다.
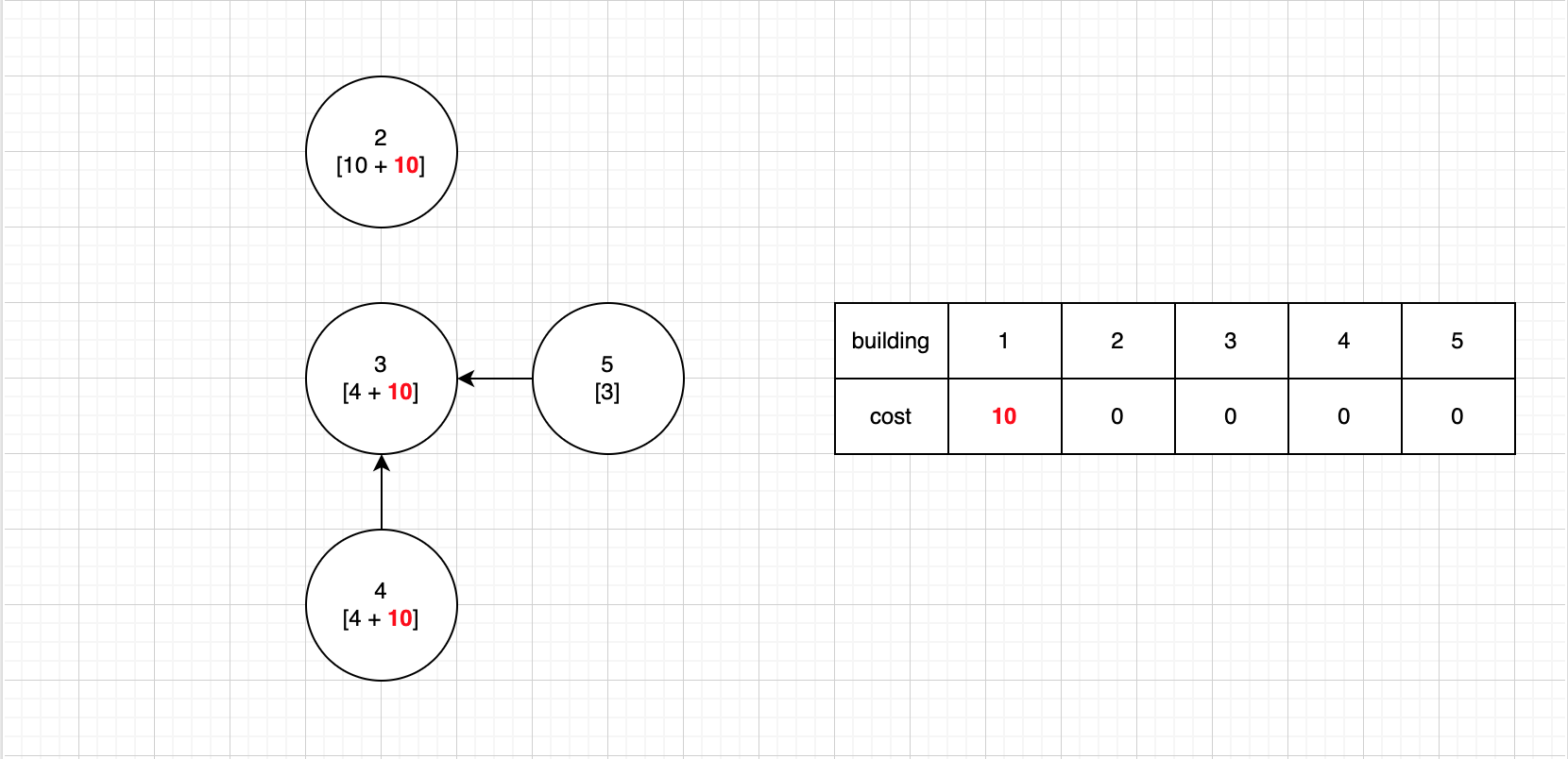
- 1번 건물을 제거할 때 현재 cost(
10)를cost리스트에 보관한다. - 1번 건물을 선행로 하는 건물에 추가 cost(
10)을 추가한다.- 추가 cost의 경우 더 큰 추가 cost가 발생하면 갱신해준다.
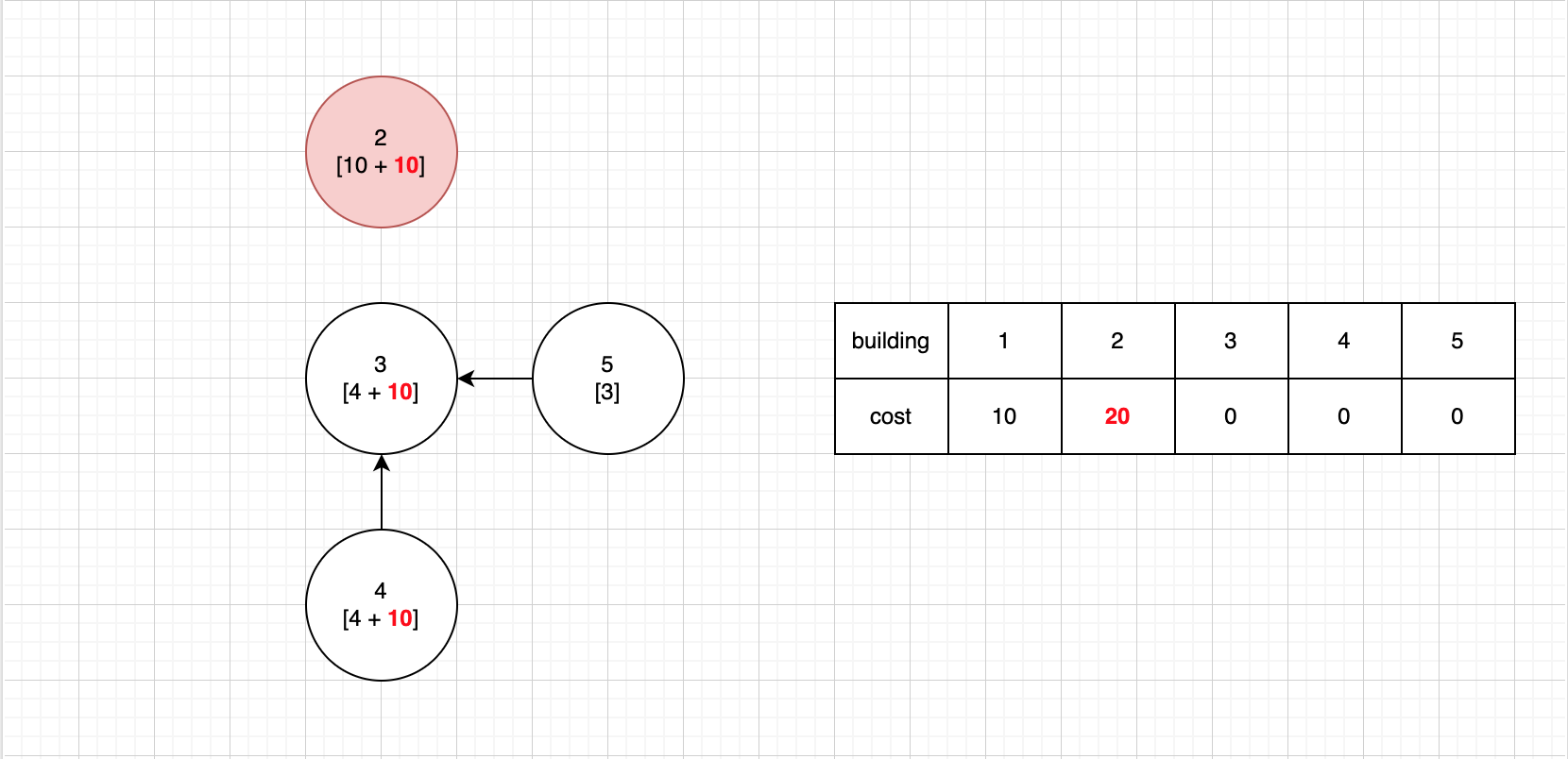
- 2번 건물의 현재 진입 차수가 0 이므로 제거한다.
- 2번 건물을 제거할 때 현재 cost(
10 + 10 = 20)을cost리스트에 보관한다. - 2번 건물을 선행 건물로 하는 건물이 없으므로 추가 cost 값 갱신은 생략한다.
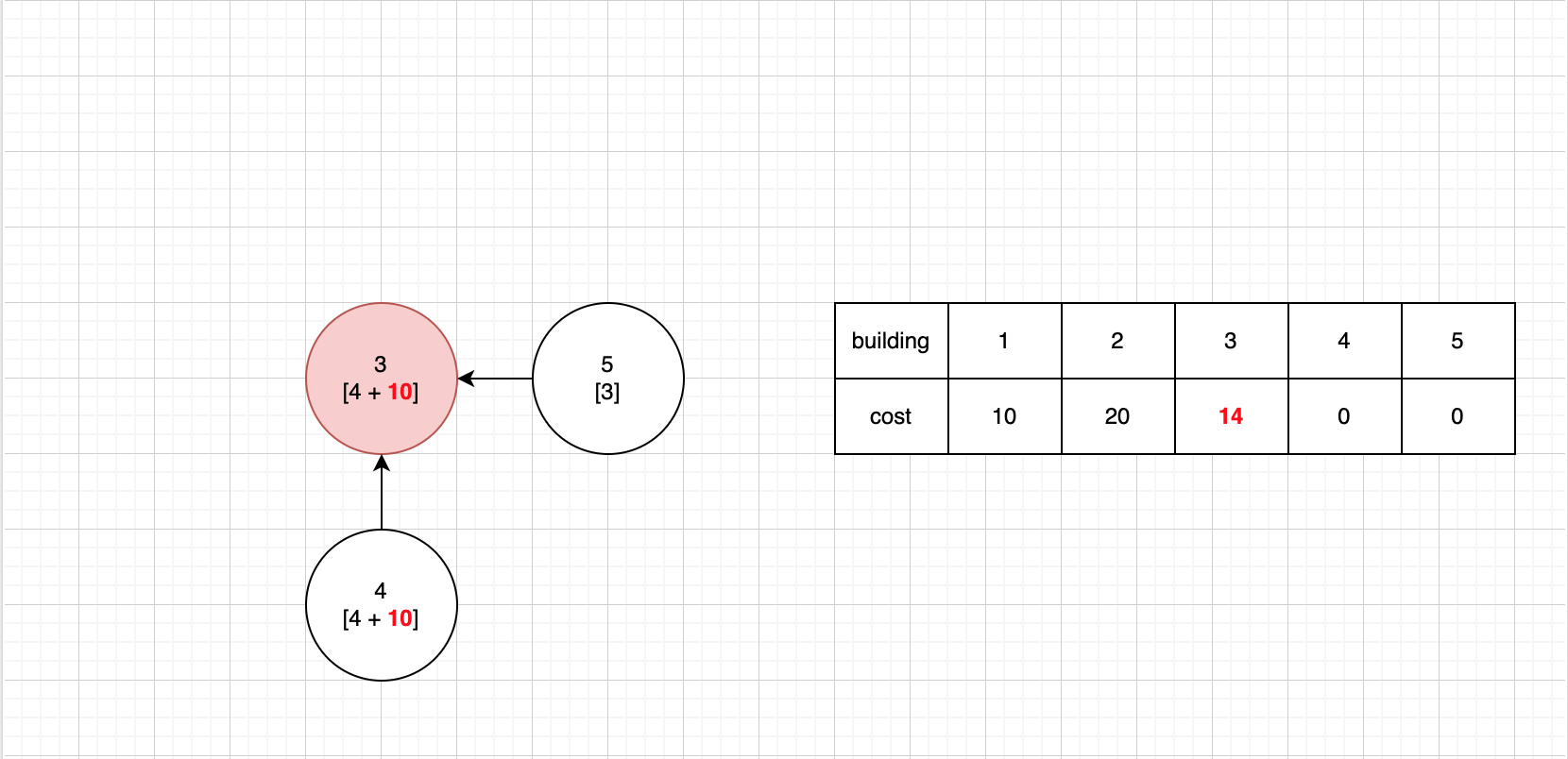
- 3번 건물의 현재 진입 차수가 0 이므로 제거한다.
- 3번 건물을 제거할 때 현재 cost(
4 + 10 = 14)을cost리스트에 보관한다.
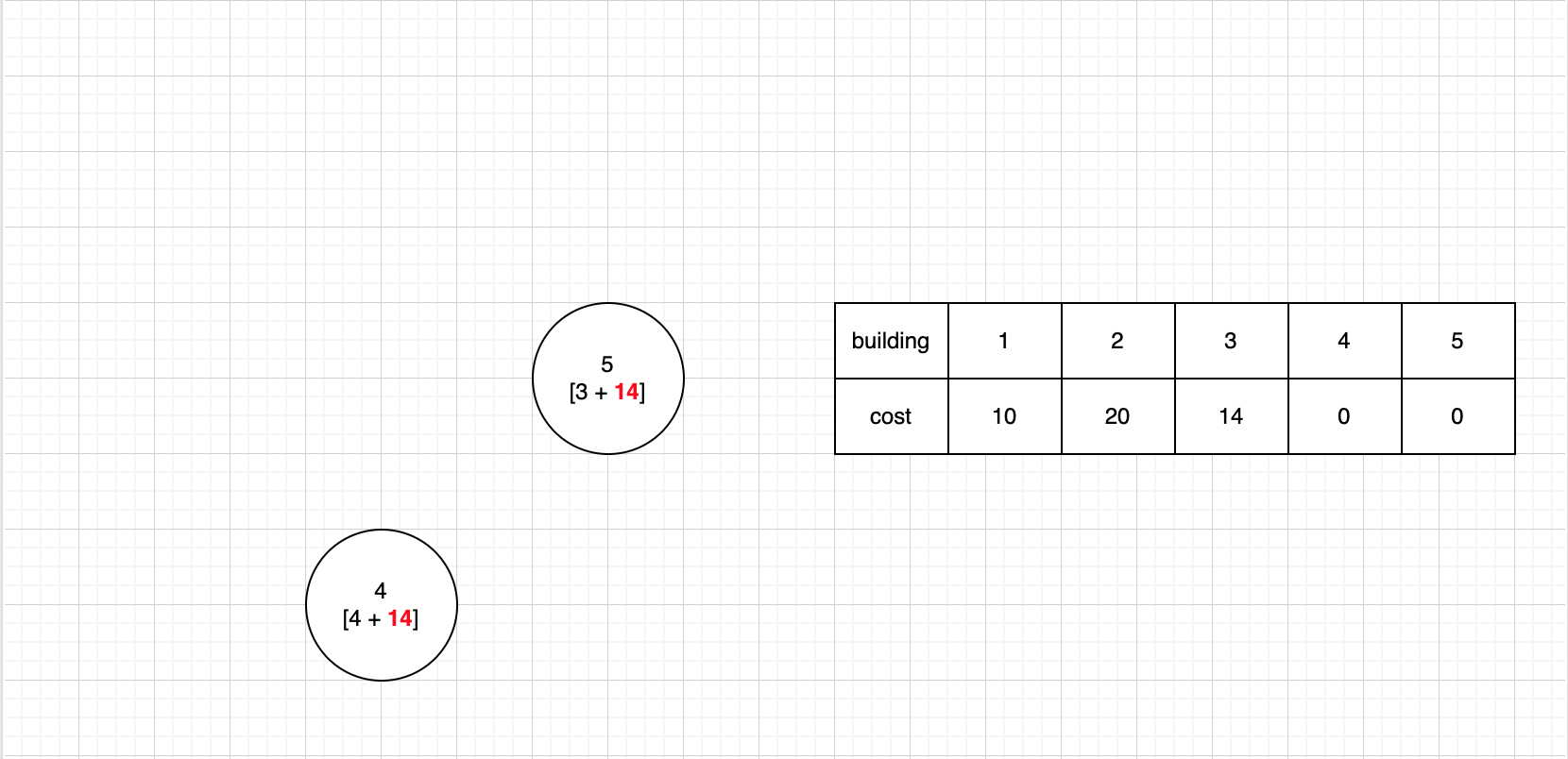
- 3번 건물을 선행으로 하는 건물에 추가 cost(
14)을 갱신한다.- 4번 건물의 현재 추가 cost는
10으로14보다 작으므로14로 값을 갱신해 준다. - 5번 건물은 현재 추가 cost가 존재하지 않으므로 추가 cost의 값을
14로 갱신해 준다.
- 4번 건물의 현재 추가 cost는
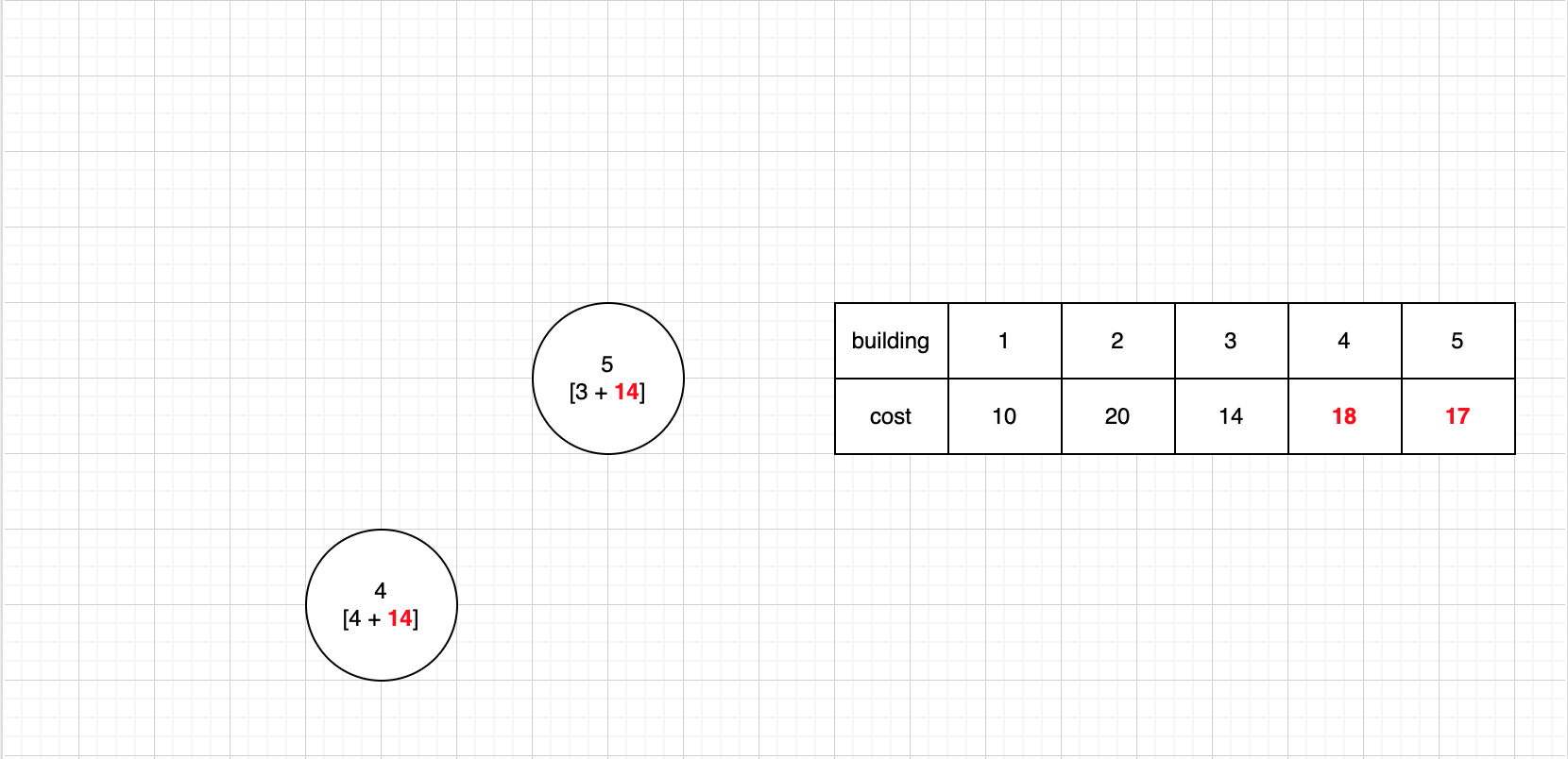
- 4번, 5번 건물은 현재 진입 차수가 0이므로 제거한다.
- 각 건물을 제거할 때 현재 cost를
cost리스트에 보관한다. - 해당 과정이 종료되면 모든 건물을 제거한 후 건물을 짓는데 필요한 시간(
cost)을 구할 수 있다.
✍ 코드
# BOJ 1516 게임 개발
# https://www.acmicpc.net/problem/1516
from sys import stdin
from collections import deque, defaultdict
def solution(N, edges):
pureCost = defaultdict(int) # 각 건물 순수 비용
prerequisite = defaultdict(list) # 선행 건물 목록
degree = [0] * (N+1) # 건물 진입 차수
for i in range(N):
pureCost[i+1] = edges[i][0] # 각 건물 순수 비용 갱신
for edge in edges[i][1:-1]:
prerequisite[edge].append(i+1) # 선행 건물 목록 갱신
degree[i+1] += 1 # 건물 진입 차수 갱신
cost = [0] * (N+1) # 건물 짓는 비용
queue = deque()
for i in range(1, N+1):
if degree[i] == 0: # 진입 차수가 없는 건물
queue.append(i) # queue에 추가
cost[i] = pureCost[i] # 건물 짓는 비용 갱신
while queue:
building = queue.popleft()
# 건물(building)을 선행으로 건물로 하는 건물(b)
for b in prerequisite[building]:
degree[b] -= 1 # 진입 차수 -1
cost[b] = max(cost[b], pureCost[b] + cost[building]) # 건물 건설에 걸리는 시간 갱신
# 선행으로 지어야 하는 건물이 존재하지 않을 경우
if degree[b] == 0:
queue.append(b)
return cost[1:]
# input
N = int(stdin.readline())
edges = [list(map(int,stdin.readline().split())) for _ in range(N)]
# res
res = solution(N, edges)
for r in res: print(r)
