[BOJ] 1719 택배 바로가기
📍 문제
명우기업은 2008년부터 택배 사업을 새로이 시작하기로 하였다. 우선 택배 화물을 모아서 처리하는 집하장을 몇 개 마련했지만, 택배 화물이 각 집하장들 사이를 오갈 때 어떤 경로를 거쳐야 하는지 결정하지 못했다. 어떤 경로를 거칠지 정해서, 이를 경로표로 정리하는 것이 여러분이 할 일이다.
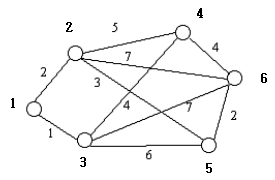
예시된 그래프에서 굵게 표시된 1, 2, 3, 4, 5, 6은 집하장을 나타낸다. 정점간의 간선은 두 집하장간에 화물 이동이 가능함을 나타내며, 가중치는 이동에 걸리는 시간이다. 이로부터 얻어내야 하는 경로표는 다음과 같다.
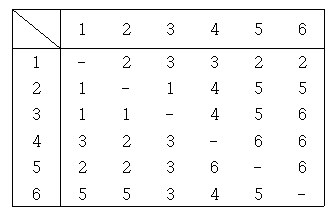
경로표는 한 집하장에서 다른 집하장으로 최단경로로 화물을 이동시키기 위해 가장 먼저 거쳐야 하는 집하장을 나타낸 것이다. 예를 들어 4행 5열의 6은 4번 집하장에서 5번 집하장으로 최단 경로를 통해 가기 위해서는 제일 먼저 6번 집하장으로 이동해야 한다는 의미이다.
이와 같은 경로표를 구하는 프로그램을 작성하시오.
📍 입력
첫째 줄에 두 수 n과 m이 빈 칸을 사이에 두고 순서대로 주어진다. n은 집하장의 개수로 200이하의 자연수, m은 집하장간 경로의 개수로 10000이하의 자연수이다. 이어서 한 줄에 하나씩 집하장간 경로가 주어지는데, 두 집하장의 번호와 그 사이를 오가는데 필요한 시간이 순서대로 주어진다. 집하장의 번호들과 경로의 소요시간은 모두 1000이하의 자연수이다.
📍 출력
예시된 것과 같은 형식의 경로표를 출력한다.
📍 풀이
💡 고찰
- 처음 풀이 방법은 힙(
heap) 자료구조를 활용한 다잌스트라(Dijkstra) 알고리즘을 적용하여 한 집하장에서 다른 집하장으로 최단경로로 화물을 이동시키기 위해 가장 먼저 거쳐야 하는 집하장 정보를 구할 수 있었다.

- 내가 푼 방법 이외에 더 좋은 문제 풀이 방법이 있는지 확인하기 위해서 구글링을 했는데 플로이드워셜(
Floyd-Warshall) 알고리즘을 확인할 수 있었다. - 다잌스트라 알고리즘을 이용한 코드와 플로이드워셜 알고리즘을 이용한 코드의 수행 시간 차이를 확인하고자 플로이드워셜 알고리즘을 적용한 코드를 작성하여 테스트를 수행하였고 아래와 같은 결과를 얻을 수 있었다.

- 플로이드워셜 알고리즘을 이용한 코드가 다잌스트라 알고리즘을 이용한 코드의 3배 빠른 효율을 보여주었다.
- 다잌스트라 알고리즘을 적용하여 문제는 해결할 수 있었지만 제일 최적의 알고리즘을 생각해내지 못한 것이 무척 아쉽다.
- 이번 문제를 통해서 배운 점은 그래프가 주어지고, 모든 노드간의 최단 거리를 구하는 문제는 플로이드워셜(
Floyd-Warshall) 알고리즘을 적용해야 한다는 것을 한번 더 복습하였다.
✍ 코드
from sys import stdin, maxsize
from collections import defaultdict
from heapq import heappop, heappush
# 다잌스트라 풀이
def solution1(n,edges):
# [0] 경로표, 가장 먼저 거쳐야 하는 집하장 표 생성
graph = [[maxsize] * (n+1) for _ in range(n+1)]
answer = [["-"] * (n+1) for _ in range(n+1)]
for i in range(1,n+1):
graph[i][i] = 0 # i → i 이동 차단
# [1] 초기 이동 경로 heap 생성
heap = []
for node, weight in edges[i]:
heappush(heap, (weight, node, node)) # (가중치, 현재 정점, 가장 먼저 거쳐야 하는 정점)
# [2] 다잌스트라 알고리즘 적용
while heap:
w, node, wayPoint = heappop(heap)
if graph[i][node] > w:
graph[i][node] = w
answer[i][node] = wayPoint
for nextNode, weight in edges[node]:
heappush(heap, (w+weight, nextNode, wayPoint))
# [3] 결과 출력
for y in range(1,n+1):
for x in range(1,n+1):
print(answer[y][x], end=' ')
print()
# 플로이드워셜 풀이
def solution2(n,edges):
# [0] 경로표, 가장 먼저 거쳐야 하는 집하장 표 생성
graph = [[maxsize] * (n+1) for _ in range(n+1)]
answer = [["-"] * (n+1) for _ in range(n+1)]
# [1] 경로표, 가장 먼저 거쳐야 하는 집하장 표 초기화
for n1, n2, w in edges:
graph[n1][n2] = w
graph[n2][n1] = w
answer[n1][n2] = n2
answer[n2][n1] = n1
for i in range(1,n+1):
graph[i][i] = 0 # i → i 이동 차단
# [2] 플로이드워셜 알고리즘 적용
for k in range(1,n+1):
for j in range(1,n+1):
for i in range(1,n+1):
if graph[i][j] > graph[i][k] + graph[k][j]:
graph[i][j] = graph[i][k] + graph[k][j] # 최단 거리 갱신
answer[i][j] = answer[i][k] # 가장 먼저 거쳐야 하는 집하장 갱신
# [3] 결과 출력
for y in range(1,n+1):
for x in range(1,n+1):
print(answer[y][x], end=' ')
print()
# input
n, m = map(int,stdin.readline().split())
edges1 = defaultdict(list)
edges2 = []
for _ in range(m):
n1, n2, w = map(int,stdin.readline().split())
edges1[n1].append((n2,w))
edges1[n2].append((n1,w))
edges2.append((n1,n2,w))
# result
solution1(n,edges1)
solution2(n,edges2)
