[Programmers] 부대복귀 바로가기
📍 문제 설명
강철부대의 각 부대원이 여러 지역에 뿔뿔이 흩어져 특수 임무를 수행 중입니다. 지도에서 강철부대가 위치한 지역을 포함한 각 지역은 유일한 번호로 구분되며, 두 지역 간의 길을 통과하는 데 걸리는 시간은 모두 1로 동일합니다. 임무를 수행한 각 부대원은 지도 정보를 이용하여 최단시간에 부대로 복귀하고자 합니다. 다만 적군의 방해로 인해, 임무의 시작 때와 다르게 되돌아오는 경로가 없어져 복귀가 불가능한 부대원도 있을 수 있습니다.
강철부대가 위치한 지역을 포함한 총지역의 수 n, 두 지역을 왕복할 수 있는 길 정보를 담은 2차원 정수 배열 roads, 각 부대원이 위치한 서로 다른 지역들을 나타내는 정수 배열 sources, 강철부대의 지역 destination이 주어졌을 때, 주어진 sources의 원소 순서대로 강철부대로 복귀할 수 있는 최단시간을 담은 배열을 return하는 solution 함수를 완성해주세요. 복귀가 불가능한 경우 해당 부대원의 최단시간은 -1입니다.
📍 제한사항
- 3 ≤ n ≤ 100,000
- 각 지역은 정수 1부터 n까지의 번호로 구분됩니다.
- 2 ≤ roads의 길이 ≤ 500,000
- roads의 원소의 길이 = 2
- roads의 원소는 [a, b] 형태로 두 지역 a, b가 서로 왕복할 수 있음을 의미합니다.(1 ≤ a, b ≤ n, a ≠ b)
- 동일한 정보가 중복해서 주어지지 않습니다.
- 동일한 [a, b]가 중복해서 주어지지 않습니다.
- [a, b]가 있다면 [b, a]는 주어지지 않습니다.
- 1 ≤ sources의 길이 ≤ 500
- 1 ≤ sources[i] ≤ n
- 1 ≤ destination ≤ n
📍 입출력 예
| n | roads | sources | destination | result |
|---|---|---|---|---|
| 3 | [[1, 2], [2, 3]] | [2, 3] | 1 | [1, 2] |
| 5 | [[1, 2], [1, 4], [2, 4], [2, 5], [4, 5]] | [1, 3, 5] | 5 | [2, -1, 0] |
📍 입출력 예 설명
입출력 예 #1
- 지역 2는 지역 1과 길로 연결되어 있기 때문에, 지역 2에서 지역 1의 최단거리는 1입니다.
- 지역 3에서 지역 1로 이동할 수 있는 최단경로는 지역 3 → 지역 2 → 지역 1 순으로 이동하는 것이기 때문에, 지역 3에서 지역 1의 최단거리는 2입니다.
- 따라서 [1, 2]를 return합니다.
입출력 예 #2
- 지역 1에서 지역 5의 최단경로는 지역 1 → 지역 2 → 지역 5 또는 지역 1 → 지역 4 → 지역 5 순으로 이동하는 것이기 때문에, 최단거리는 2입니다.
- 지역 3에서 지역 5로 가는 경로가 없기 때문에, 지역 3에서 지역 5로 가는 최단거리는 -1입니다.
- 지역 5에서 지역 5는 이동할 필요가 없기 때문에, 최단거리는 0입니다.
- 따라서 [2, -1, 0]을 return합니다.
📍 풀이
📌 문제 풀이
sources 라는 출발지에서 destination 이라는 목적지로 이동할 수 있는 최단 거리를 구하는 문제이다.
최단 거리를 구하는 문제에 적용할 수 있는 알고리즘은 다익스트라, 플로이드워셜 알고리즘이다.
destination 이라는 목적지 1곳에 대한 정보만을 필요로 하므로 모든 경로의 최단 거리를 구하는 플로이드워셜 알고리즘 대신 더 효율이 좋은 다익스트라 알고리즘을 적용하여 문제를 해결하였다.
🧷 그래프
입출력 예 #2 의 지역을 그래프로 표현한 것이다.
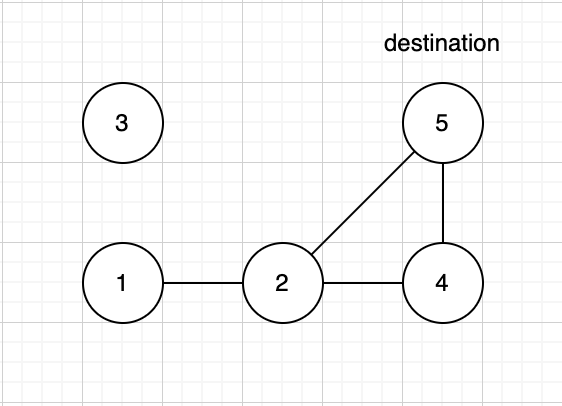
문제에서 주어진 그래프는 양방향 그래프이기 때문에 sources 에서 destination 으로 이동하는 동선과 destination 에서 sources 로 이동하는 동선은 같다.
따라서 destination 에서 시작하는 다른 지역으로 이동하기 위한 최단거리를 구하는 다익스트라 알고리즘을 구현하면 각 sources 에 대한 최단 거리를 구할 수 있다.
🧷 destination 다익스트라 알고리즘
- 만약 다익스트라 알고리즘에 대해서 모른다면 📒 다익스트라 알고리즘 을 참고
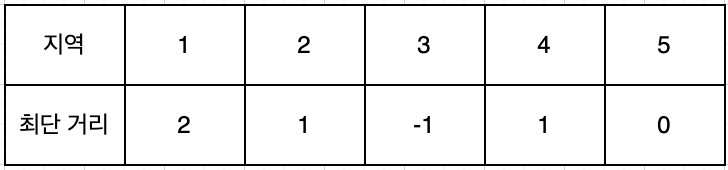
destination 인 5 에서 시작하여 다른 지역으로 이동하기 위한 최단 거리를 다익스트라로 구한 결과이다.
이를 이용하여 sources 인 [1, 3, 5] 에서 5 로 이동하기 위한 최단 거리([2, -1, 0])를 구할 수 있다.
✍ 코드
from collections import defaultdict, deque
from sys import maxsize
def solution(n, roads, sources, destination):
answer = []
# graph 초기화
graph = defaultdict(list)
for s, e in roads:
graph[s].append(e)
graph[e].append(s)
# 다익스트라
move = [maxsize] * (n+1)
move[destination] = 0
queue = deque([destination])
while queue:
node = queue.popleft()
for nextNode in graph[node]:
if move[nextNode] > move[node] + 1:
move[nextNode] = move[node] + 1
queue.append(nextNode)
# 결과
for source in sources:
answer.append(move[source] if move[source] != maxsize else -1)
return answer