
[Codility] 3. TapeEquilibrium
문제 링크
TapeEquilibrium
문제 요약
정수 P가 |(A[0] + A[1] + ... + A[P − 1]) − (A[P] + A[P + 1] + ... + A[N − 1])|로 정의되어 있다. 즉 정수 N이 주어졌을 때 배열에서 A[N]을 포함하는 왼쪽의 원소를 합한 값에서, A[N]의 오른쪽에 위치하는 원소의 값을 뺀 수의 절대값이 P이다.
가능한 모든 P(N)에 대해 최소값을 구하라.
요구사항
정수 N의 범위가
N is an integer within the range [2..100,000]
이므로 Time Error에 주의해야 한다.
시간복잡도는 항상 패턴을 잘 짜야하는 것 같다.
무지성으로 반복 돌려버리면 답이 안나온다..
초기 코드
import Foundation
import Glibc
public func solution(_ A : inout [Int]) -> Int {
var arr = Int()
var arr2 = Int()
var num: Int = Int.max
if A.count < 3 {
return abs(A[0] - A[1])
}
for i in 1..<A.count {
A[0...i-1].forEach {
arr += $0
}
A[i..<A.count].forEach {
arr2 += $0
}
num = abs(arr-arr2) < num ? abs(arr-arr2) : num
arr = 0
arr2 = 0
}
return num
}
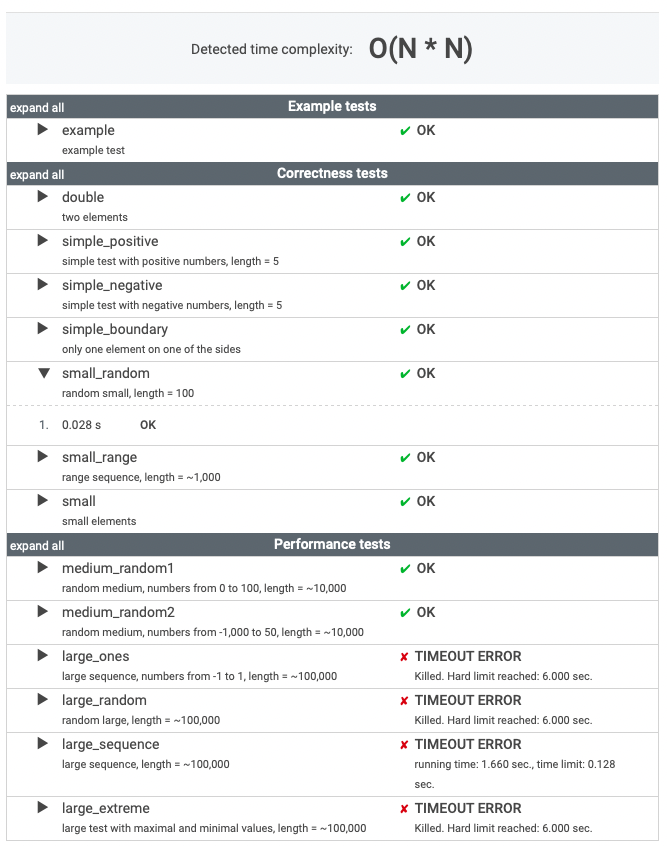
역시 무지성 코드는 어림도 없지
수정 코드
import Foundation
import Glibc
public func solution(_ A : inout [Int]) -> Int {
var P = Int()
var sum = Int()
var minDiff = Int.max
A.forEach {
sum += $0
}
for (idx, _) in A.enumerated() {
if idx > 0 {
P += A[idx-1]
minDiff = abs((P*2) - sum) < minDiff ? abs((P*2) - sum) : minDiff
}
}
return minDiff
}
항상 짜릿해...
