[MST#1] 크루스칼(Kruskal)

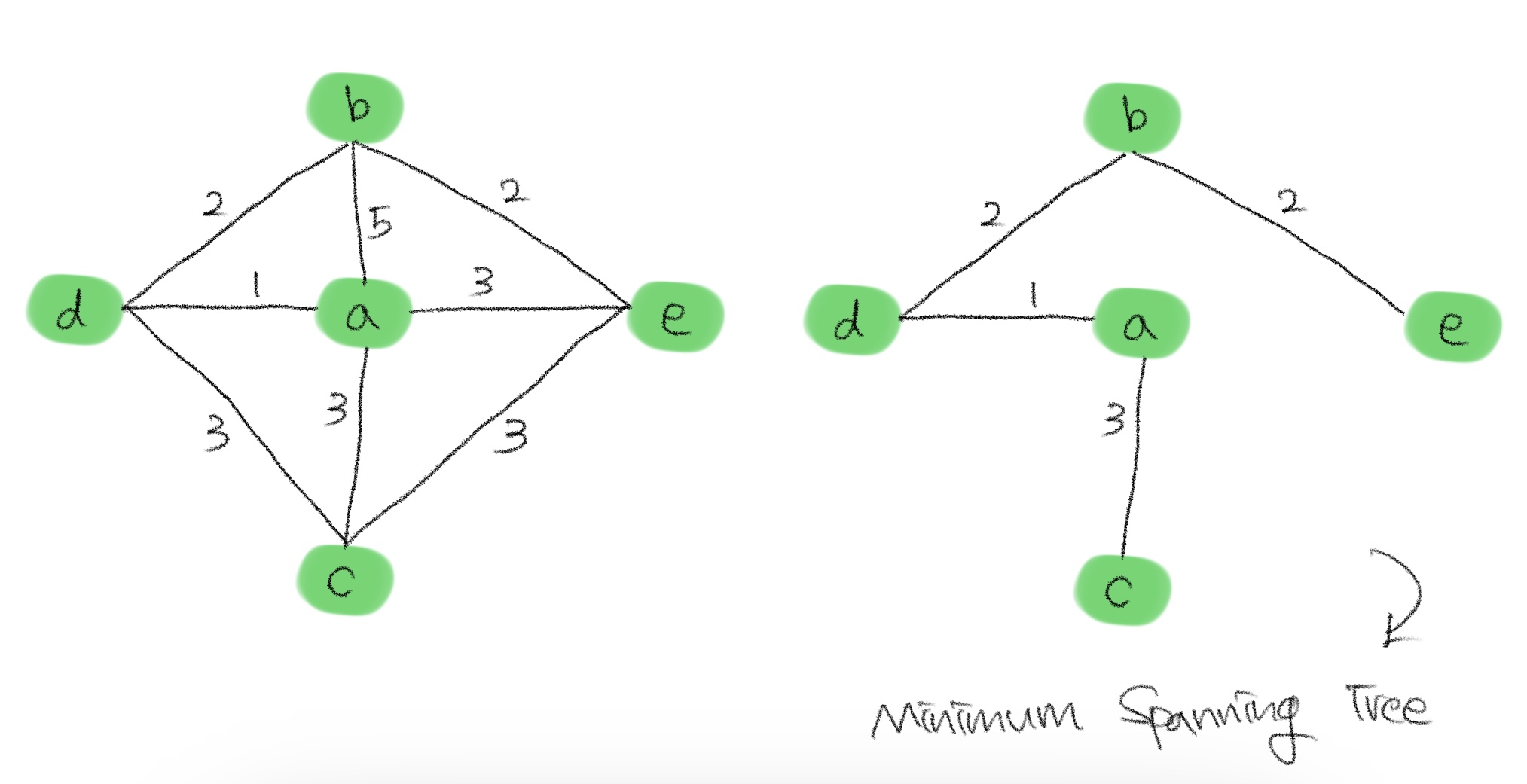
최소신장트리(Minimum Spanning Tree)

최소신장트리란 신장트리 중 간선의 가중치의 합이 최소가 되는 트리이다.

MST 알고리즘

• 크루스칼(kruskal)
• 프림(Prim)

신장트리(Spanning Tree)
그래프 상에서 모든 노드가 사이클 없이 연결된 부분 그래프

• 그래프의 모든 정점 포함
• 정점의 개수가 n개이면, 간선의 개수는 n-1개

---

크루스칼(Kruskal)

간선을 중심으로 최소신장트리를 구하는 알고리즘으로 간선이 적을 때는 프림 알고리즘보다 유리하다.

크루스칼 탐색과정

1. 간선들의 가중치를 오름차순으로 나열한다.
2. 가중치가 작은 순서대로 경로를 선택해서 노드를 잇는다.
3. 모든 노드의 탐색이 끝나면 종료한다.

주의할점
사이클이 생기면 안 된다.

크루스칼 구현방법

• 유니온 파인드 : 사이클 여부를 확인하기 위해 사용
  (시간복잡도 - O(ElogV)) 간선 수 : E / 노드 수 : V

// graph[i][0] : 출발노드
// graph[i][1] : 도착노드
// graph[i][2] : 가중치

public static int kruskal(int[][] graph, int[] parent) {
	int cost = 0;
    
	for(int i=0; i<graph.length; i++) {
		if(find(parent, graph[i][0]) != find(parent, graph[i][1])) {
			cost += graph[i][2];
			union(parent, graph[i][0], graph[i][1]);
		}
	}
	
    return cost;
}