Summary

• 강화학습에서 DQN의 확장 버전인 Rainbow라고 불리는 논문에서 적용된 방법 중 하나

Noisy networks

Exploration

• 자세한 예제를 적고싶지만, 저작권 문제가 없는 적당한 이미지가 없으므로 생략

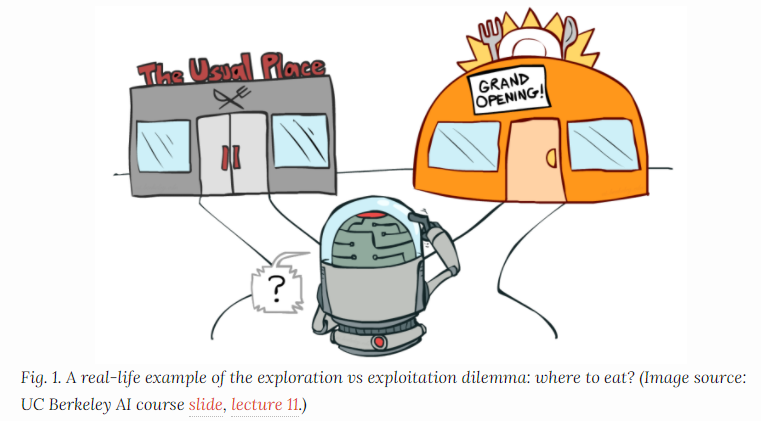
• 강화학습에서 흔히 얘기되는 Exploitation vs Exploration 개념

  • Exploitation: 맛집으로 알려진 음식점을 방문 (그림의 왼쪽)
  • Exploration: 새로운 음식점을 방문 (그림의 오른쪽)

• DQN (Deep Q Network)
  

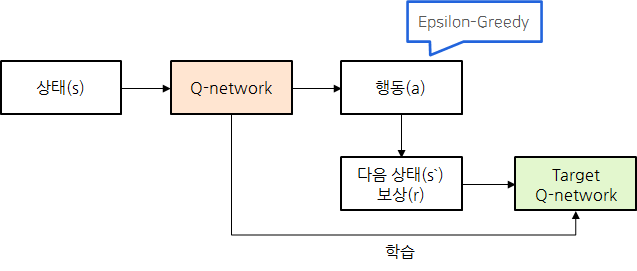
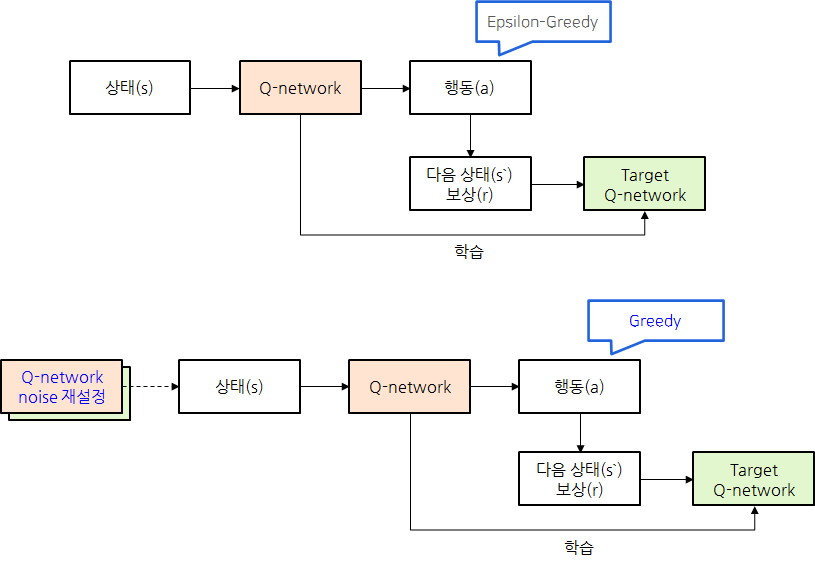
• DQN 등에서 사용하는 방법으로는 Epsilon-Greedy Algorithm이 있음.

  • 항상 Q값이 높은 Action을 선택하지만, 입실론의 작은 확률로 랜덤 Action을 선택
  • ex) 항상 맛집을 가지만, 입실론의 작은 확률로 새로운 음식점을 방문

• 그런데 이러한 exploration 방법들은 아래와 같은 단점(혹은 약점)이 존재하는데

  • 1. Heuristic한 방법임
  • 2. State-independent하게 noise를 적용함
    • ex) 입실론의 확률로 랜덤하게 움직이는 것은 현재 상태와 아무런 연관이 없음.

• 그렇다면 Non heuristic하고 State-dependent하게 noise를 어떻게 적용할 수 있을까?
  

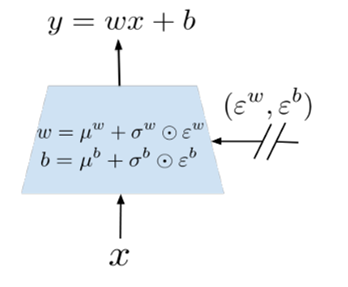
  • Neural network의 weight에 gaussian noise를 적용해서 exploration을 하자
  • 시그마라는 학습 변수를 두고 noise를 스케일링함
  • 1. 그러면 휴리스틱하지 않으면서
  • 2. 상태를 입력으로 받아 시그마를 학습해서 사용하므로 State-dependent 함

Noisy Networks

Paramters and Variables

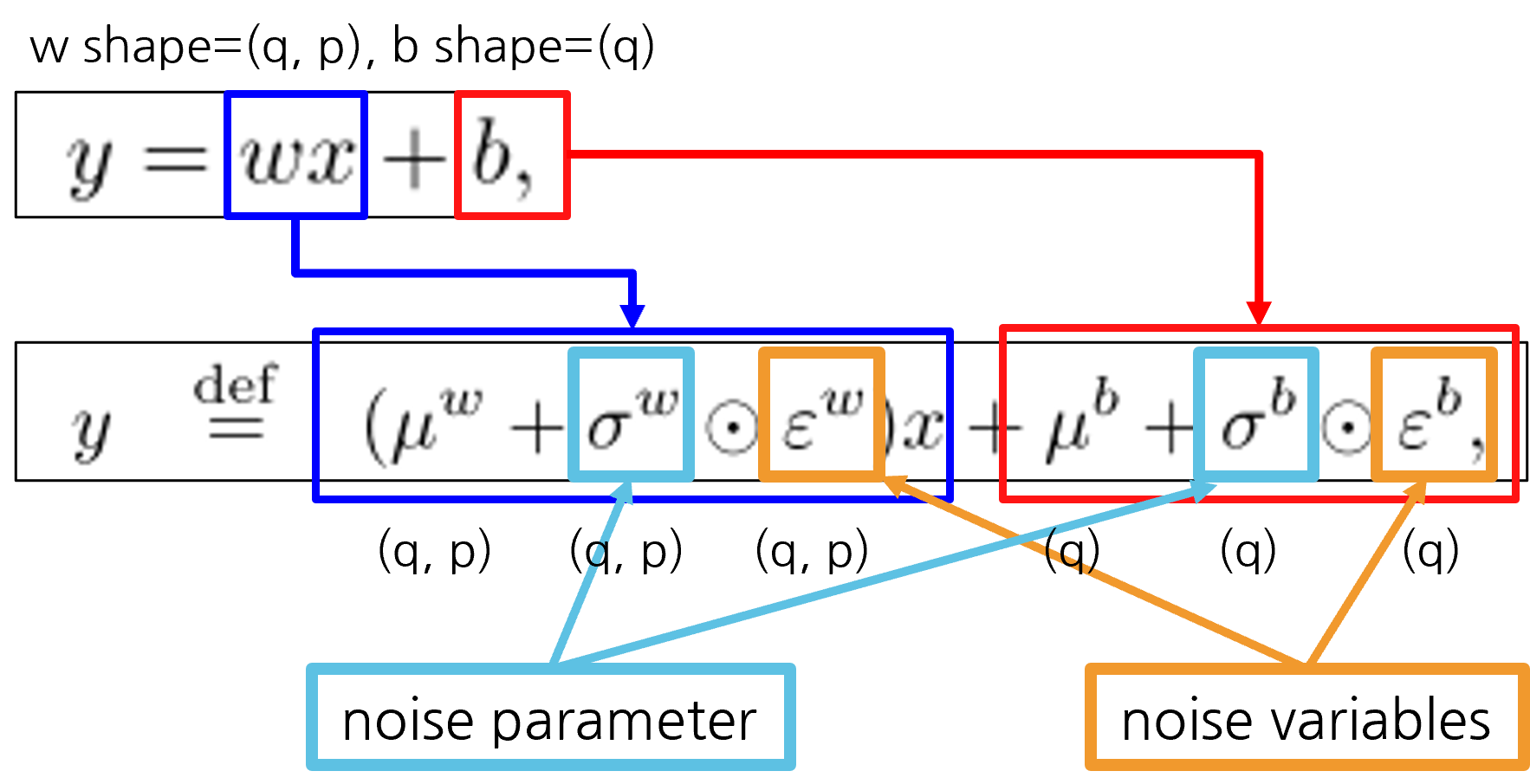
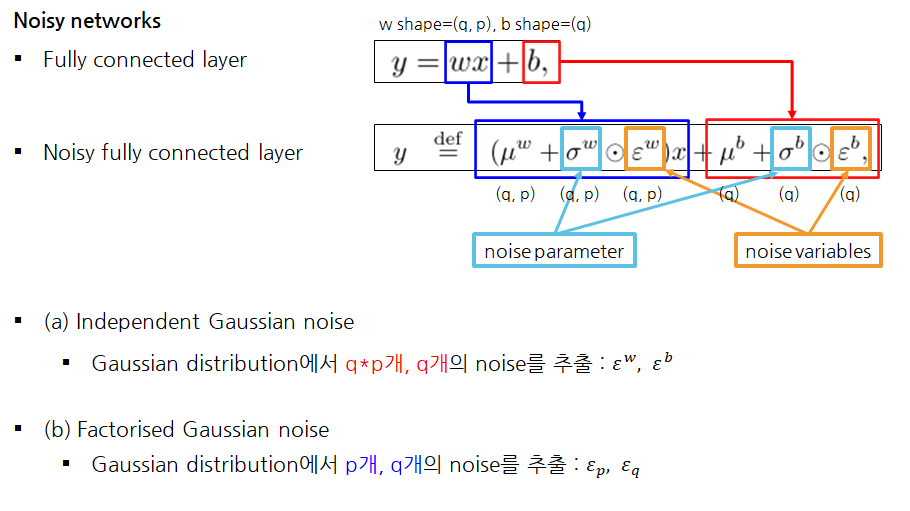
• FC vs Noisy FC
  

  • FC에서 입력의 크기는 p, 출력의 크기는 q라고 하면, Noisy FC에서는 아래와 같이 shape을 가짐

• Learnable parameters vs Noise variables
  

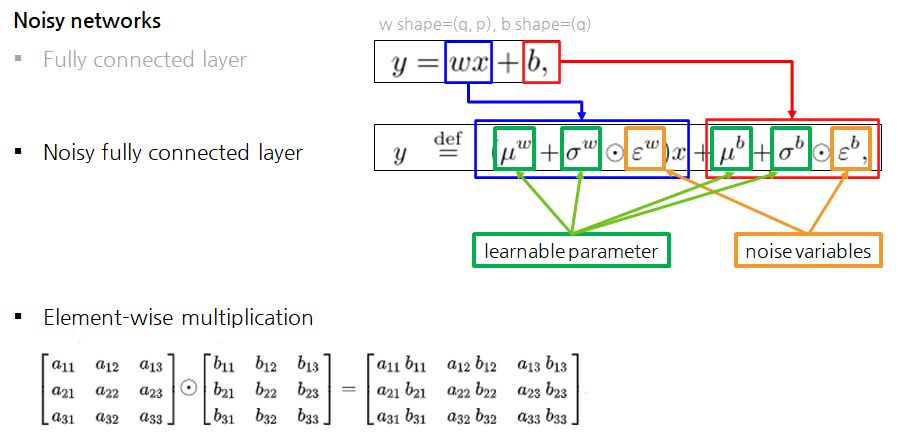
  • Noisy FC에서 𝜇는 FC의 w라고 생각하기
  • 달라지는 건 Noise variables이 추가되고, 이를 스케일링하는 시그마 학습변수가 추가됨

• Noise paramters vs Noise variables
  

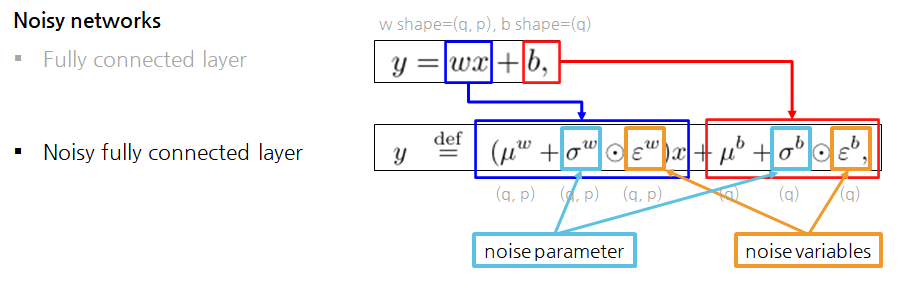
Independent Gaussian noise

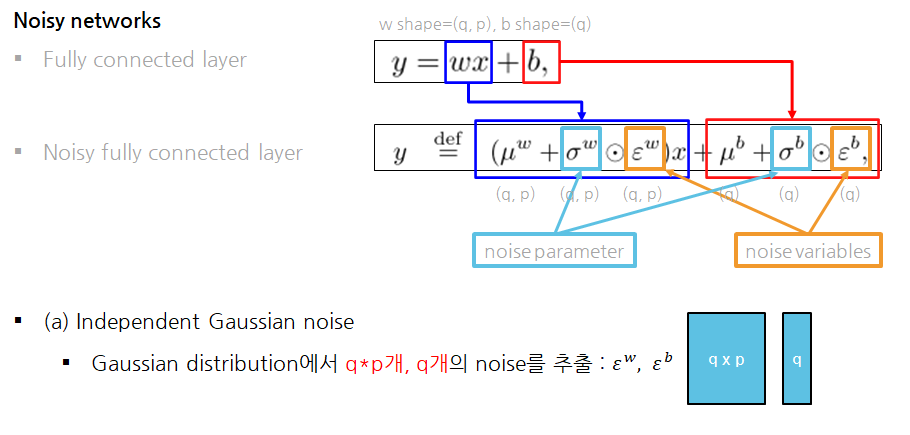
• 직관적으로 가우시안 분포에서 필요한 shape만큼 노이즈를 추출
• weight의 입실론는 qp개, bias의 입실론 q개 필요하므로, qp개와 q개를 뽑아서 사용

Factorised Gaussian noise

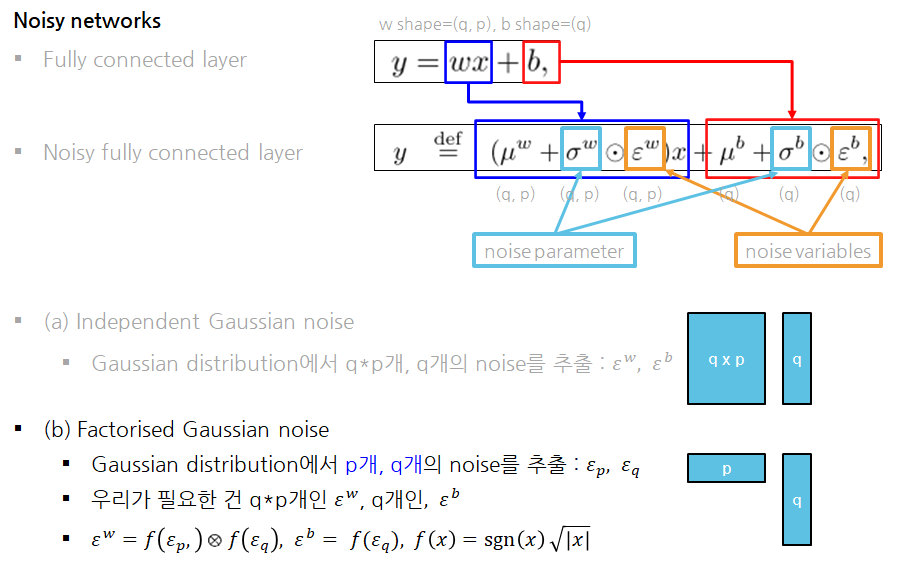
• 논문에서는 Noise를 뽑는 한 가지 방법을 더 제시했음.
  • 싱글 스레드 환경에서 q*p개 + q개의 노이즈를 가우시안 분포에서 뽑는 것이 생각보다 시간이 오래 걸림
  • 그래서 가우시안 분포에서 이것보다 더 적은 개수의 노이즈를 뽑아서 노이즈를 뽑는 시간을 단축시키려는 것이 목적
  • p개와 q개의 noise만으로 p*q개의 noise를 만드는 방법
• f(x)를 통과시키는 이유 (논문에 정확한 설명은 없지만)
  
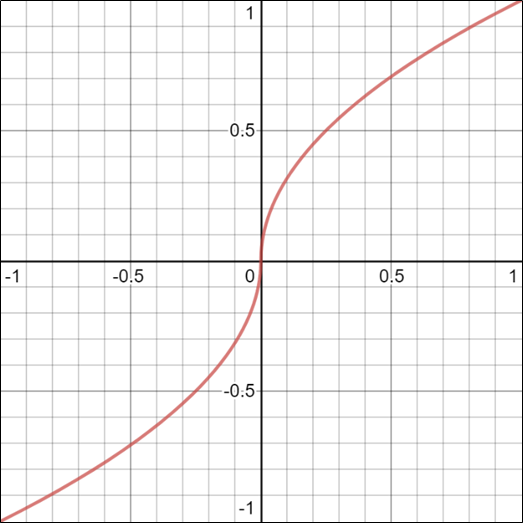
  • 입실론이 작은 값으로 뽑혔을 때 두 번 곱하면 noise가 너무 작아지므로 ..
  • 제곱근을 취하고 부호를 다시 붙여주어 크기만 키우려는 목적으로 생각됨.

Summary

• 정리하자면 Factorised 가우시안 노이즈 방법은 p개와 q개의 noise를 뽑아서 사용하는 방법
  

  • 여기서 잠깐, Factorised라는 의미를 왜 붙였을까를 해석해보자면
    • 인수분해나 분해라는 의미가 있음
    • 처음에 입력과 출력의 크기인 p, q만큼 noise를 뽑고
    • noise인 입실론을 p*q로 구하기 때문에 그렇게 부르는 것 같음
    • 논문에서는 (a)방법을 반대로 unfactorised 가우시안 노이즈라고 부르기도 함

• Independent Gaussian noise vs Factorised Gaussian noise
  

  • 원래 저자들의 의도는 (a) 방법
  • single thread agent는 noise를 뽑는 시간조차 overhead라 생각하여, (b)를 고안

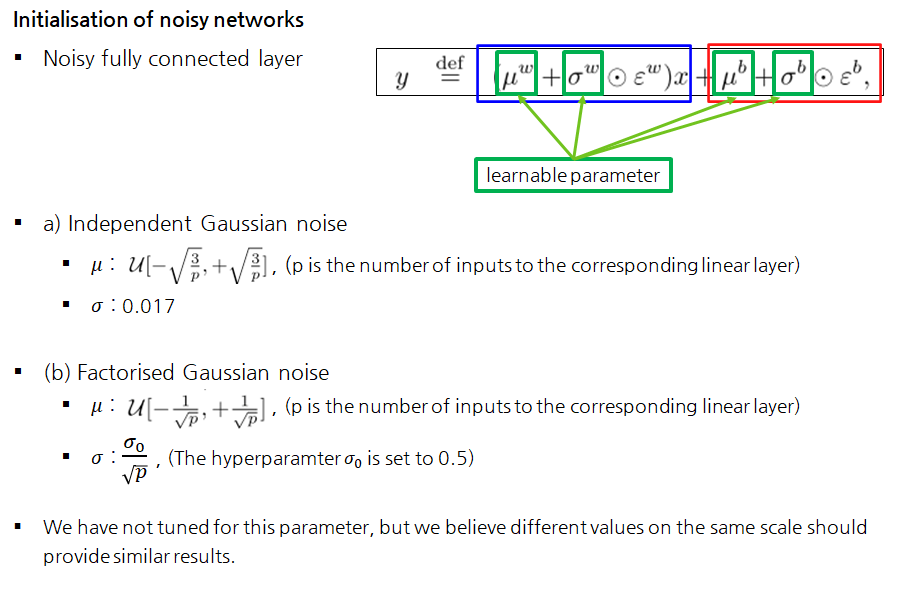
Initialisation of noisy networks

DQN vs Noisy networks

Experiments

• DQN, Dueling, A3C (Baseline) vs Noisy Networks
  
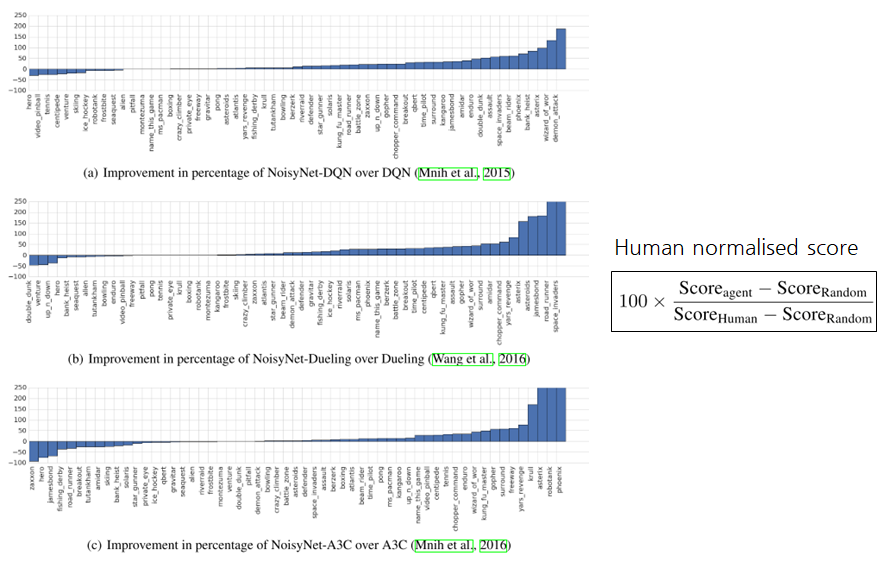
  • 양수: Noisy Networks를 적용한 후 성능이 좋아짐
  • 음수: Noisy Networks를 적용한 후 성능이 나빠짐
  • 대체로 NoisyNet을 끼얹은 후에 성능이 더 좋아짐
  • 사용한 메트릭으로는 Human normalised score라는 것을 사용함
    • 사람이 한 결과와 랜덤 액션으로 했을 때 얻을 수 있는 결과를 사용

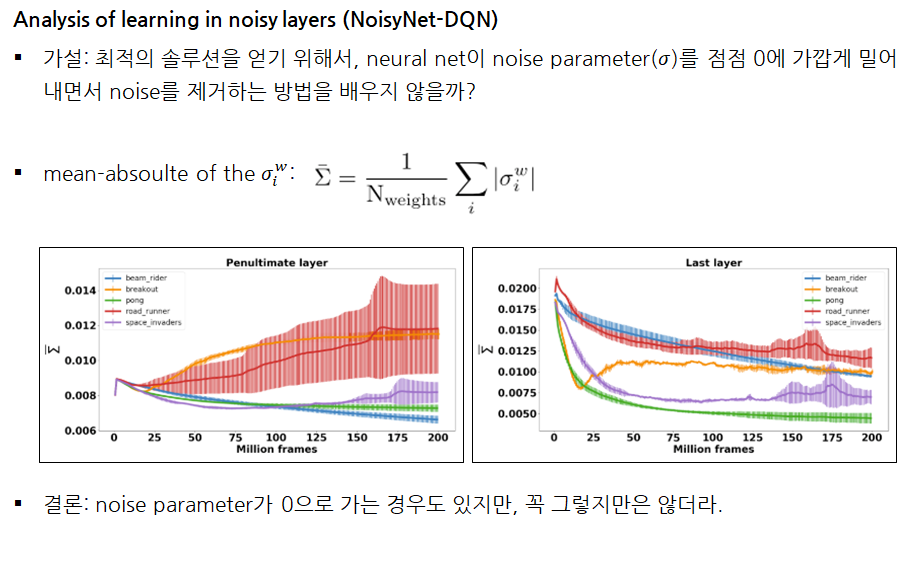
Conclusion

• 성능

  • super human 성능을 달성하거나, 대체로 baseline 보다 성능이 좋아진다.
  • 하지만 게임 or 시드에 따라서 working하지 않는 경우도 있다.

• 트레이닝

  • noise를 주입할 양(𝜎)이 학습되기 때문에, 하이퍼파라미터 튜닝을 덜 해도 된다.

• 기타

  • 추가적인 gradient 계산 비용은 큰 성능 향상에 비하면 적은 편이다.
  • 목적 함수가 변경된 것과 Exploration을 분리해서 분석해볼 필요가 있다.
  • 트레이닝이 끝난 이후 실제로 사용할 때는 𝜇 만 사용한다.

Reference

• 논문

  • ✔ NoisyNet: https://arxiv.org/abs/1706.10295
  • Rainbow: https://arxiv.org/abs/1710.02298

• 참고 자료

  • ✔ https://www.slideshare.net/ssuserbd7730/pyconkr-2018-rladventureto-the-rainbow
  • ✔ https://www.slideshare.net/KyunghwanKim27/rainbow-2nd-dlcat-in-daejeon

• 코드 구현

  • ✔ https://github.com/wenh123/NoisyNet-DQN/blob/e93c385916e81944ba1861f848d03811756a1a49/tf_util.py
  • ✔ https://github.com/go2sea/NoisyNetDQN/blob/master/myUtils.py
  • ✔ https://github.com/higgsfield/RL-Adventure/blob/master/5.noisy%20dqn.ipynb
  • ✔ https://github.com/a7b23/noisynetDQN/blob/master/noisy_dqn.py
  • ✔ https://github.com/Shmuma/ptan/blob/master/samples/rainbow/lib/dqn_model.py
  • ✔ https://github.com/Shmuma/ptan/blob/master/samples/rainbow/04_dqn_noisy_net.py