지난 에피소드에 이어서 진행한다.
Initial Example
Graphical User Interface
우리가 작성한 lemma들이 옳은지 어떻게 증명할까?
$ tamarin-prover interactive FirstExample.spthy기본적으로 오류 없이 컴파일이 잘 되면, http://localhost:3001 주소로 Tamarin GUI가 열린다. 브라우저에서 확인해보자.
Installation의 경우, Tamarin github나 manual을 참고하자.
macOS, Linux의 경우 brew 패키지 인스톨러를 이용한 설치가 가장 간편하다.
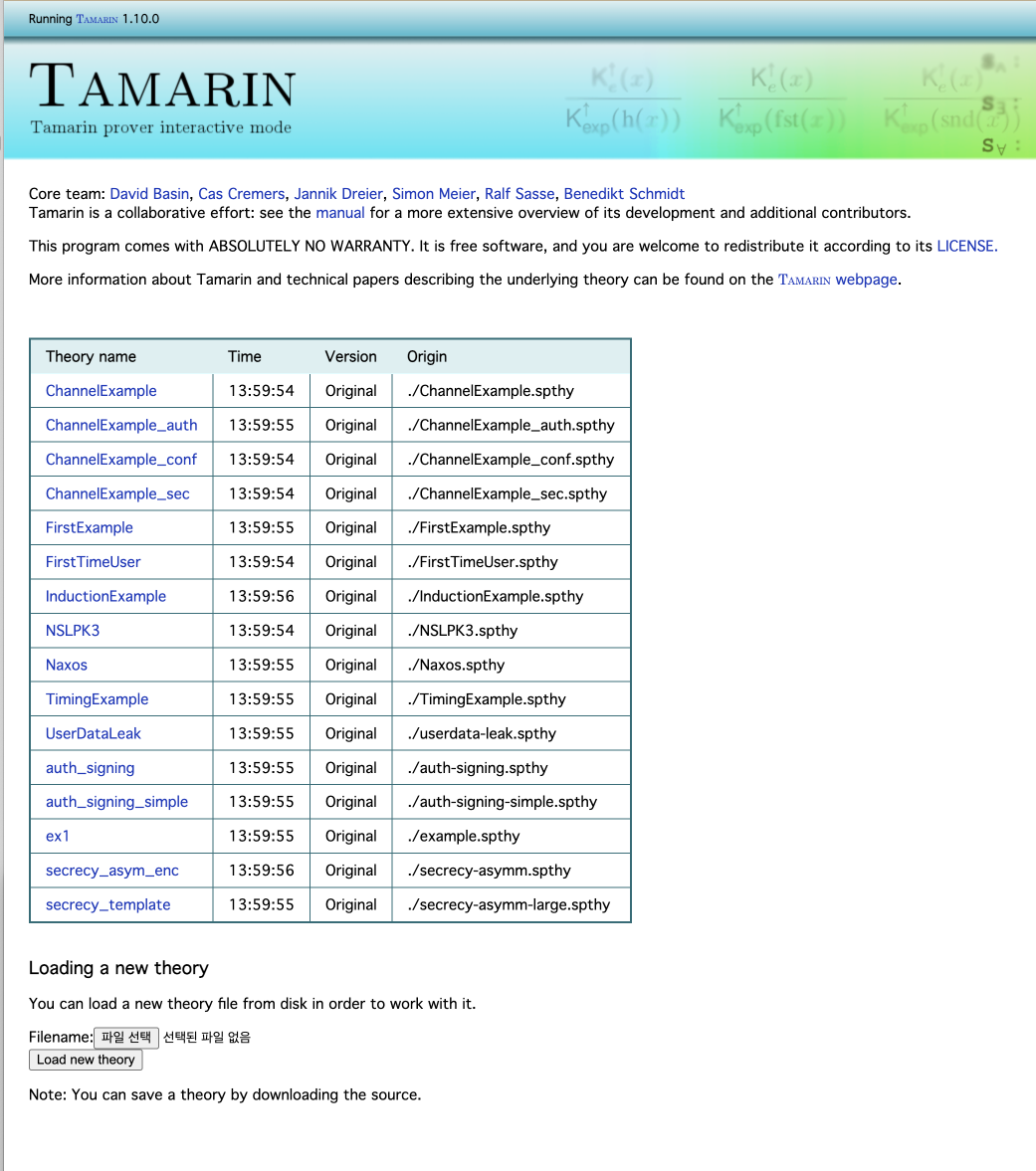
실행 시 위와 같은 화면을 볼 수 있다. 분석을 원하는 파일을 클릭하여 확인하면 된다.
'FirstExample'파일을 클릭하여 분석해보자.
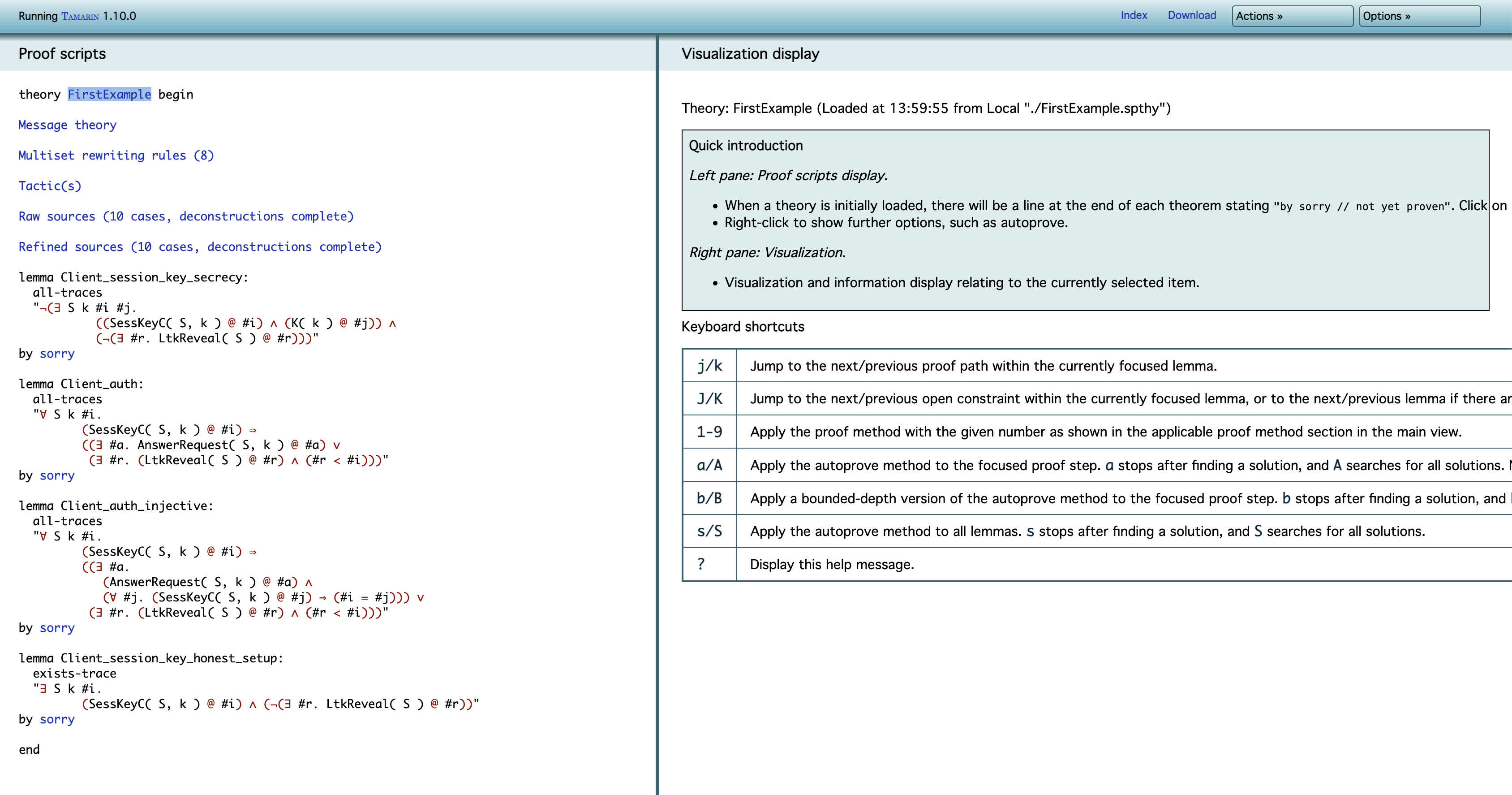
화면 왼쪽은, theory가 표시되며, 여기에는 다음과 같은 요소들이 포함된다.
- 메시지 이론(Message theory): 공격자(adverary)를 설명하는 부분
- 멀티셋 재작성 규칙(Multiset rewriting rules): 프로토콜을 설명하는 규칙과 제약조건
- 원시 소스(Raw source) 및 정제 소스(Refined source): 분석 과정에서 사용되는 소스들
- 증명하고자 하는 정리(lemmas): 검증해야 할 명제들
화면 오른쪽에는, 몇 가지 메뉴와 단축키들이 적혀 있다.
화면 왼쪽의 Message theory를 클릭하면 화면 오른쪽에 메시지 이론들이 나열된다.
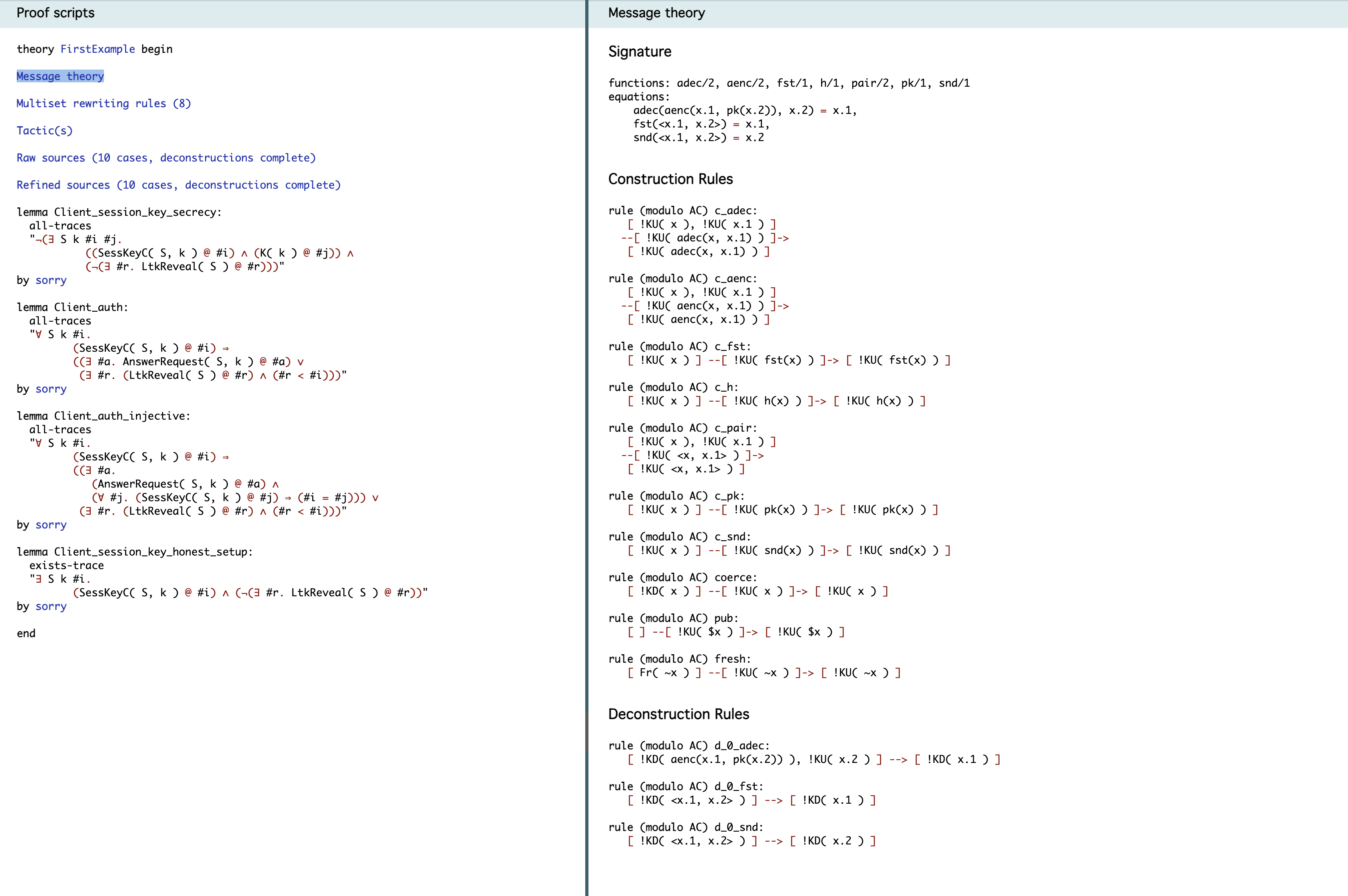
Signature로 시작하는 부분에서, 모든 functions와 equations들을 확인할 수 있다.
이것들은 사용자 정의(user-defined)이거나 built-ins를 사용하여 임포트된 것이다.
Tamarin은 자동으로 괄호쌍을 위해 pair라는 함수를 추가한다. 또한, fst와 snd를 함께 추가한다. 각각 pair의 first 요소와 second 요소를 반환하는 방정식이다.
fst(<x.1, x.2>) = x.1에서 볼 수 있듯이 <, >는 pair의 약칭(shorthand)이다.
Construction Rules의 규칙들은 공격자가 적용할 수 있는 기능들(functions)을 나타낸다.
rule (modulo AC) ch:
[ !KU(x) ] --[ !KU(h(x)) ]-> [ !KU(h(x)) ]직관적으로 이 규칙은 다음을 의미한다.
- 전제(premise)에서
!KU(x)가 존재한다는 것은 공격자가x를 알고 있음을 의미한다. - 결론(conclusion)에서
!KU(h(x))가 존재한다는 것은 공격자가x를 해싱하여h(x)를 계산할 수 있다는 것을 의미한다.
즉, 공격자는 어떤 값을 알고 있다면, 그 값의 해시도 계산할 수 있다.
라벨(label)에 포함된 !KU(h(x))는 이 과정이 증명 과정에서 논리적으로 추론될 수 있도록 기록됨을 의미한다.
마지막으로 Deconstruction rules는 함수를 적용함으로써 큰 terms로 부터 공격자가 추출할 수 잇는 term들을 의미한다.
rule (modulo AC) dfst:
[ !KD(<x.1, x.2>) ] --> [ !KD(x.1) ]이 규칙은 공격자가 <x.1, x.2> 쌍을 알고있다면, 첫 번째 값인 x.1을 추출할 수 있다는 것을 의미한다.
이것은 pair에 대한 fst의 적용과 fst(<x.1, x.2>) equation의 결과이다.
!KD() 와 !KU()는 모두 공격자의 지식을 의미하는데 둘을 구분하는 이유는, Tamarin의 논리적 추론을 보다 효율적으로 만들기 위해서이다.
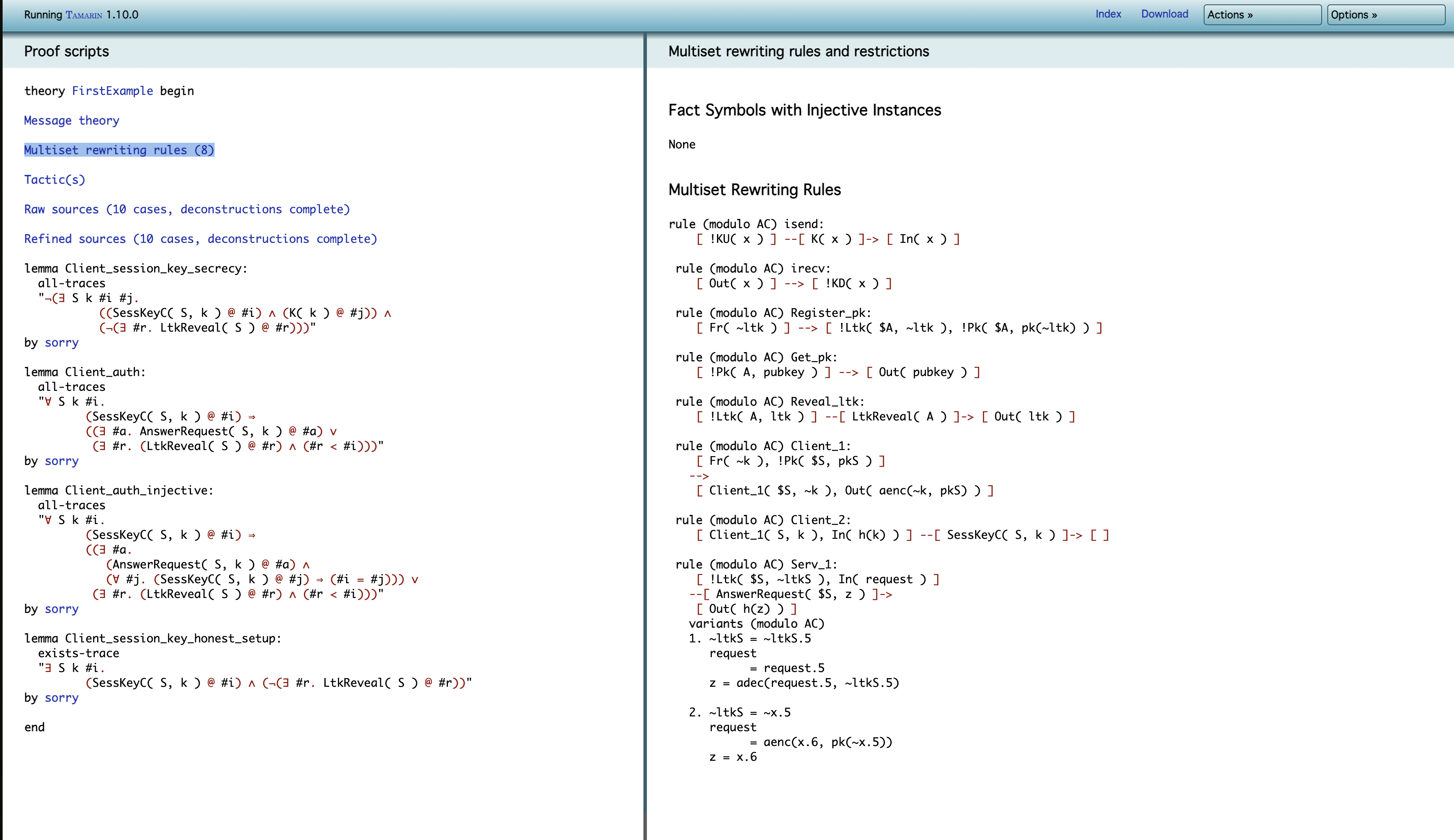
위 그림은 Multiset rewriting rules를 클릭하면 볼 수 있는 화면이다.
화면의 오른쪽은 프로토콜의 재작성 규칙들과 2개의 추가적인 규칙들:isend, irecv을 볼 수 있다. 이 추가적인 규칙들은 프로토콜의 입/출력과 공격자의 추론 간의 인터페이스를 제공한다.
isend는 !KU(x)를 In(x) 프로토콜의 입력값으로 전달한다.
(공격자가 자신이 알고 있는 정보를 프로토콜에 보낼 수 있음을 나타냄)
반면, irecv는 Out(x) 프로토콜의 출력값을 받아 공격자의 지식(!KD(x))으로 전달한다. (프로토콜이 보낸 데이터를 공격자가 수신할 수 있음을 나타냄)

Serv_1규칙은 2개의 variants(변이) (modulo AC)를 가진다는 것에 유의해라.
정확한 의미는 cryptographic messages 섹션에서 설명하겠다.
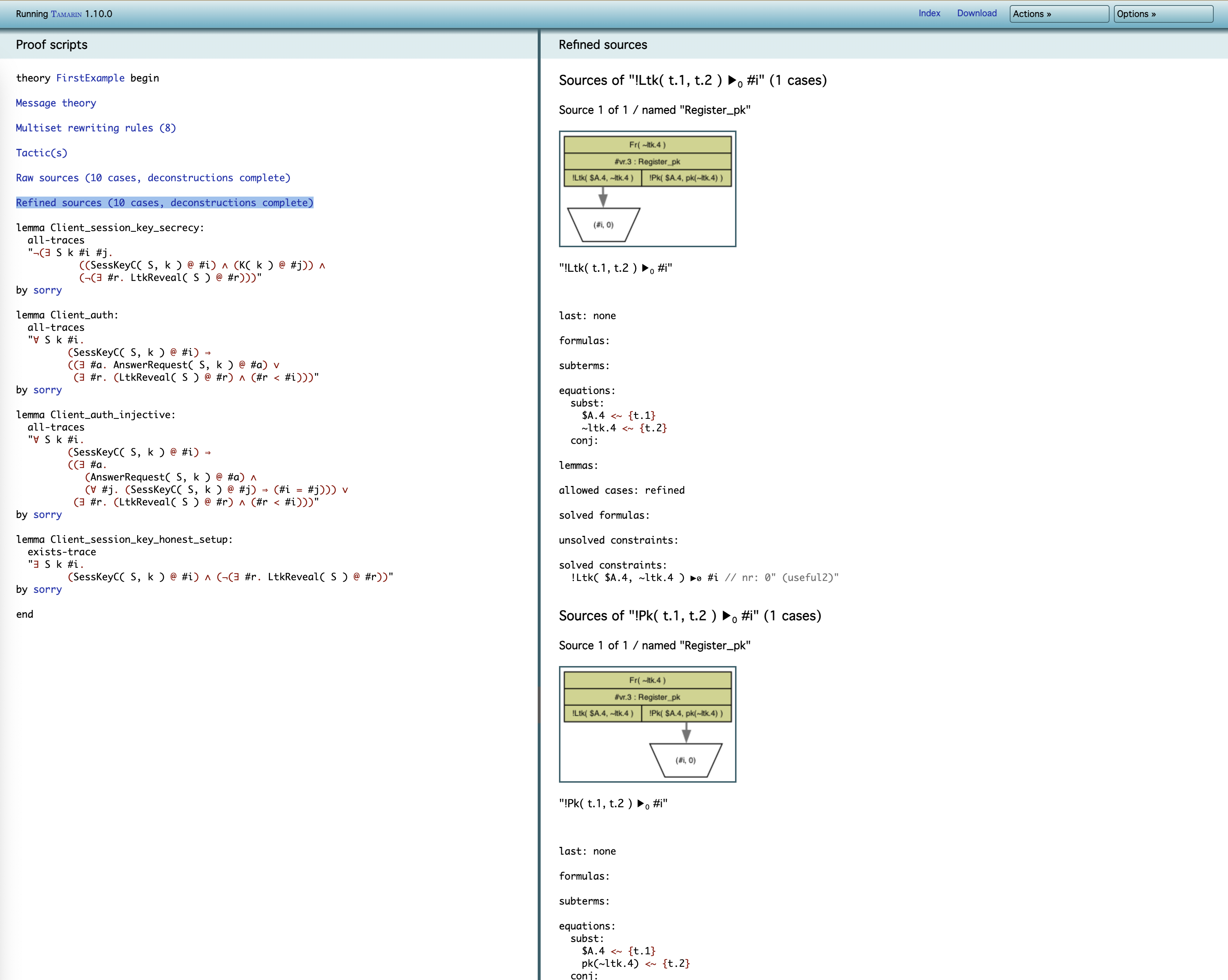
Refined sources를 클릭하면 위와 같은 화면을 볼 수 있다.
Tamarin은 내부적인 추론 효율성을 높이기 위해서 사전 계산(Precomputation) 과정에서 경우 구분(Case distinctions)을 수행한다.
경우 구분은 특정한 사실(fact)의 모든 가능한 출처(sources)를 미리 분석하는 과정이다.
즉, 어떤 규칙(또는 규칙의 조합)이 해당 사실을 생성할 수 있는지 미리 계산한다.
이렇게 사전 계산된 정보는 Tamarin의 역방향 탐색(backward search) 과정에서 활용된다.
이를 통해 같은 사실을 반복적으로 계산하는 비효율성을 방지할 수 있다.

예를 들어, Tamarin은 !Ltk(t.1, t.2) 사실의 가능한 출처가 단 하나뿐임을 알려준다.
즉, 이 사실은 Register_pk 규칙에서만 생성될 수 있다.
- green box :
Register_pk의 인스턴스를 나타냄 - trapezoid(사다리꼴) :
!Ltk(t.1, t.2)사실의 sink(최종 도착지)를 의미함
경우 구분(case distinction)
이 예시에서는 단 하나의 규칙(Register_pk)만 해당 사실을 생성할 수 있지만,
경우에 따라 여러 개의 규칙 인스턴스가 존재할 수도 있음
또한, 하나의 경우 구분 내에 여러 개의 가능한 시나리오(다양한 규칙 조합)가 포함될 수 있음
기술 정보(the technical information)
Tamarin이 경우 구분을 어떻게 계산했는지, 해결해야할 추가적인 제약(방정식, 치환 등)이 있는지에 대한 세부 정보를 제공한다.
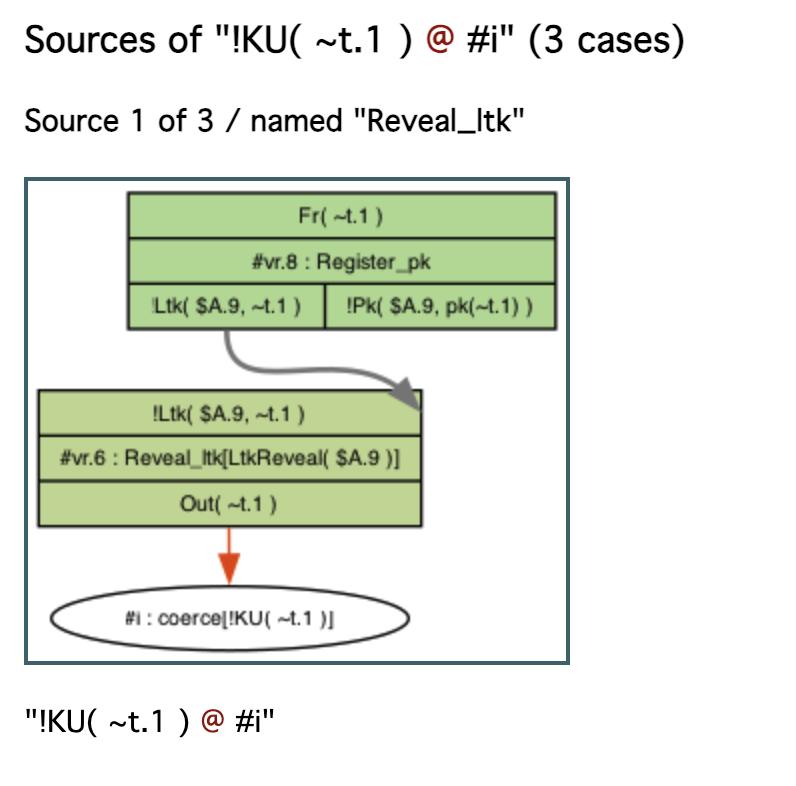
3개의 출처(sources)를 가지는 !KU(~t.1) 사실이 있다. 첫 번째는 Reveal_ltk 규칙이다. 이 규칙은 !Ltk 사실을 생성하기 위한 Register_pk 규칙의 인스턴스를 요구한다.
나머지 2개의 source들은 아래 그림으로 대체한다.
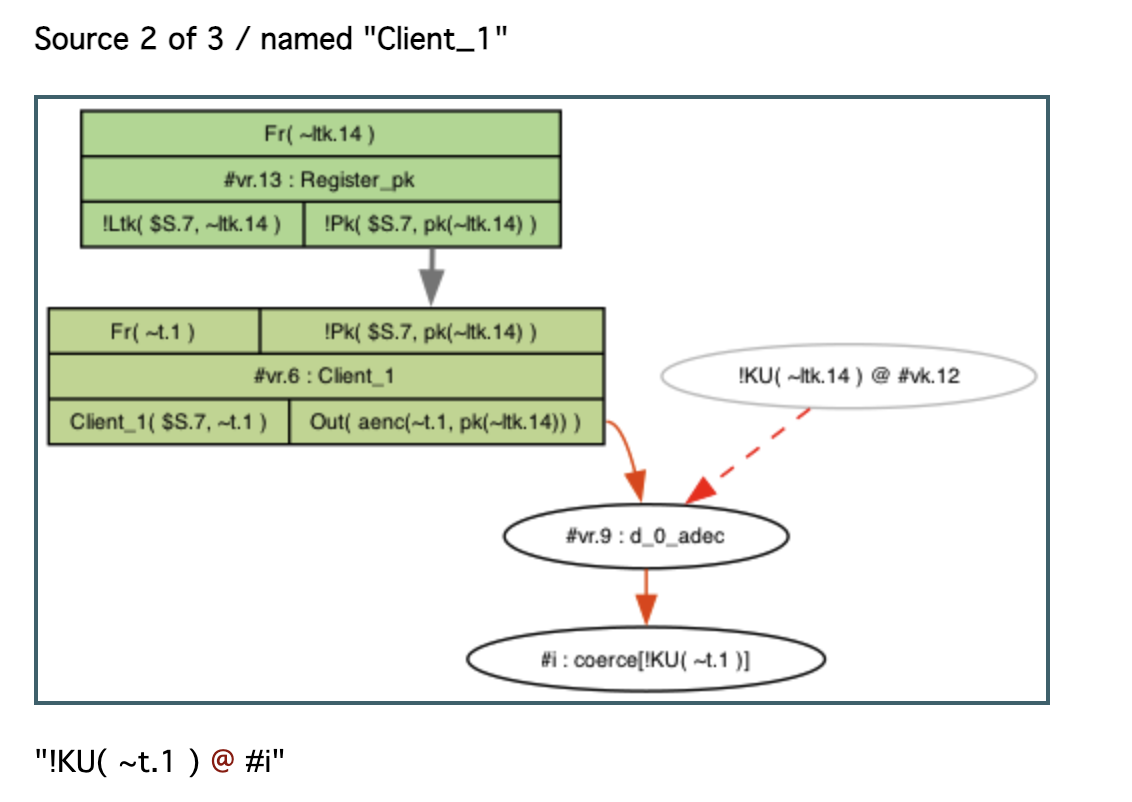

이제 interactive 모드에서 어떻게 lemma들을 검증하는지 볼 것이다. 검증하기 위해서, sorry(검증이 시작되지 않았다는 것을 나타냄)를 클릭한다.
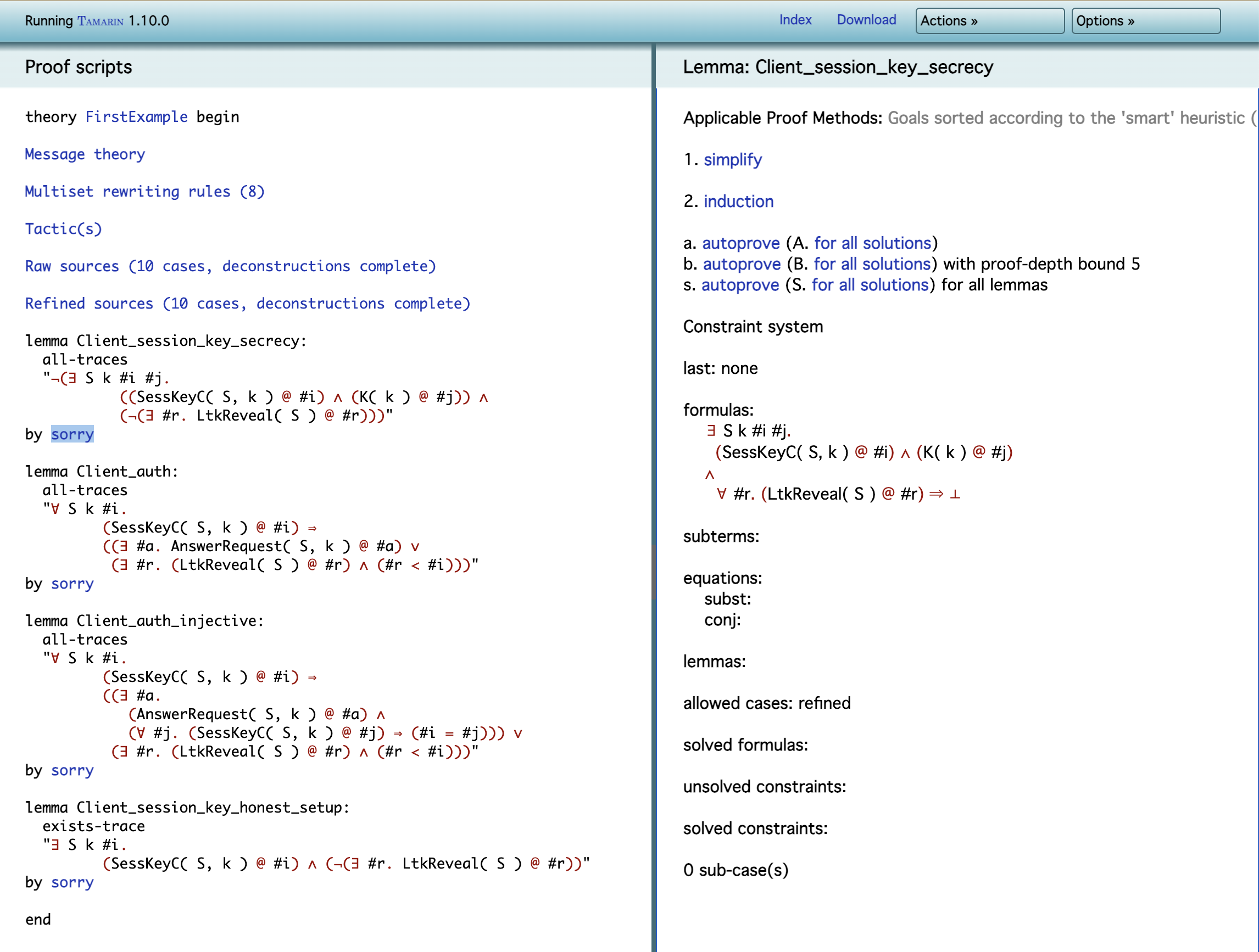
Tamarin은 제약 해결(constraint solving)을 사용하여 lemma를 검증한다. 구체적으로, Tamarin은 프로토콜과 해당 보안 속성(property)에 대해 알고 있는 정보를 계속해서 정제(refine)하면서 분석을 진행한다.
이 과정은 제약 시스템(constraint system)을 기반으로 수행된다.
증명 과정의 결과는 두 가지로 나뉜다:
- 모든 가능한 경우에서 해당 속성이 성립함을 증명 → 정리(lemma)가 참임이 입증됨.
- 반례(counterexample)를 찾아 속성이 성립하지 않음을 증명 → 정리(lemma)가 거짓임을 입증하고, 취약점이 존재할 가능성을 시사.
즉, Tamarin은 가능한 모든 시나리오를 분석하여 lemma가 참인지 거짓인지 판별하는 방식으로 보안 프로토콜을 검증한다.
우리는 이제 위에서부터 가능한 검증 절차와 제약 시스템의 현재 상태를 가진다. 아직 검증을 하지 않았기 때문에 제약 시스템은 빈 상태이다. 검증은 항상 단순화 과정( 1.simplify)이나 귀납 과정(2.induction)에서 부터 시작된다.
- simplify : lemma를 초기 제약 시스템(initial constraint system)으로 변환하며, 해당 제약 시스템을 해결해야 한다.
- induction : 실행(trace)의 길이에 대한 귀납(induction)을 사용하여 lemma를 증명하는데 필요한 제약을 생성한다.
simplify를 클릭하면 다음과 같은 결과를 얻을 수 있다.
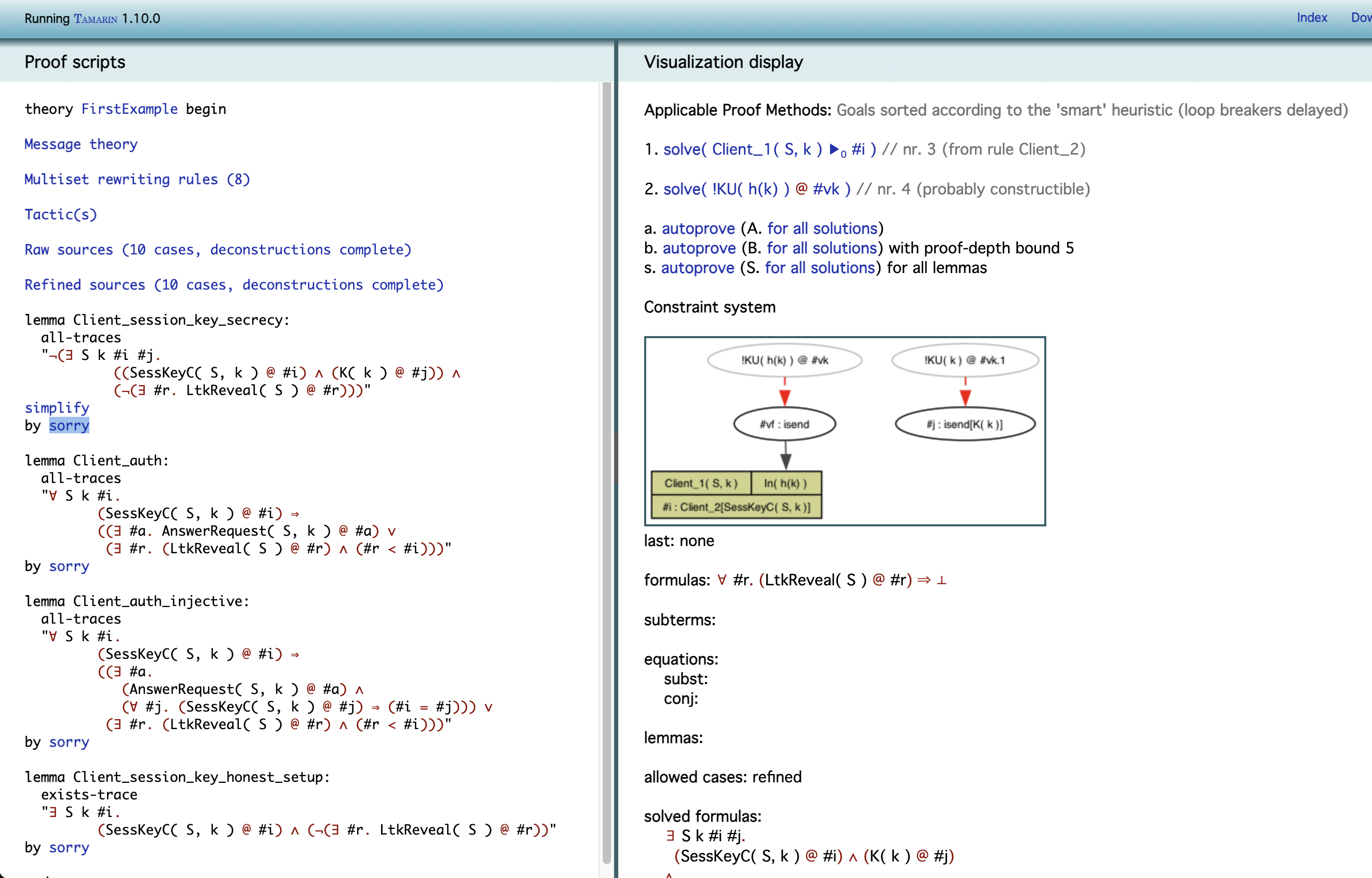
Tamarin이 lemma를 제약 시스템으로 변환했다. 이제 lemma의 반례를 찾으려한다. 즉, 다음 조건을 만족하는 프로토콜 실행(protocol execution)을 찾는다.

SessKeyC(S, k)액션이 존재K(k)액션이 존재- 하지만,
LtkReveal(S)이 사용되지 않음
이것은 그래프로 시각화되어 있다.
SessKeyC(S, k) 액션을 얻는 것은 오직 Client_2 규칙의 인스턴스를 사용하는 것이다.
K(k) 규칙은 라운드 박스(공격자의 논리적 추론은 항상 라운드 박스를 사용하여 나타낸다)로 표현되었다.
그래프 아래에는 다음과 같은 공식을 볼 수 있다.
∀ #r. (LtkReveal(S) @ #r) ⇒ ⊥
이제 LtkReveal(S)의 발생은 모순으로 이어질것이라고 말한다.
증명을 마치기 위해서, 우리는 다음 해결할 제약들을 선택함으로써 수동적으로 계속할 수도 있고 autoprove 명령을 호출할 수 도 있다. 우리는 2개의 제약을 해결해야 한다. (Client_1(S, k), KU(k)) 두 제약 모두 현재 종료되지 않은 제약 시스템의 규칙들을 위한 전제조건(premises)들이다.
GUI에서 제공되는 증명 방법은 autoprove명령어에서 사용되는 것과 동일한 휴리스틱(heuristic)에 따라 정렬된다.
- 항상 첫 번째 증명 방법을 선택하면,
autoprove명령어가 생성하는 증명과 동일한 증명이 수행됨 - 하지만, 일반적으로 보안 프로토콜 검증 문제는 결정 불가능(undecidable)하기 때문에, 일부 프로토콜 및 속성(Property)에 대해 알고리즘이 종료되지 않을 수 도 있다.
해당 예제에서는 첫 번째 제약을 여러 번 클릭하거나, autoprover를 사용하면 다음과 같은 최종 상태(final state)에 도달하게 된다.
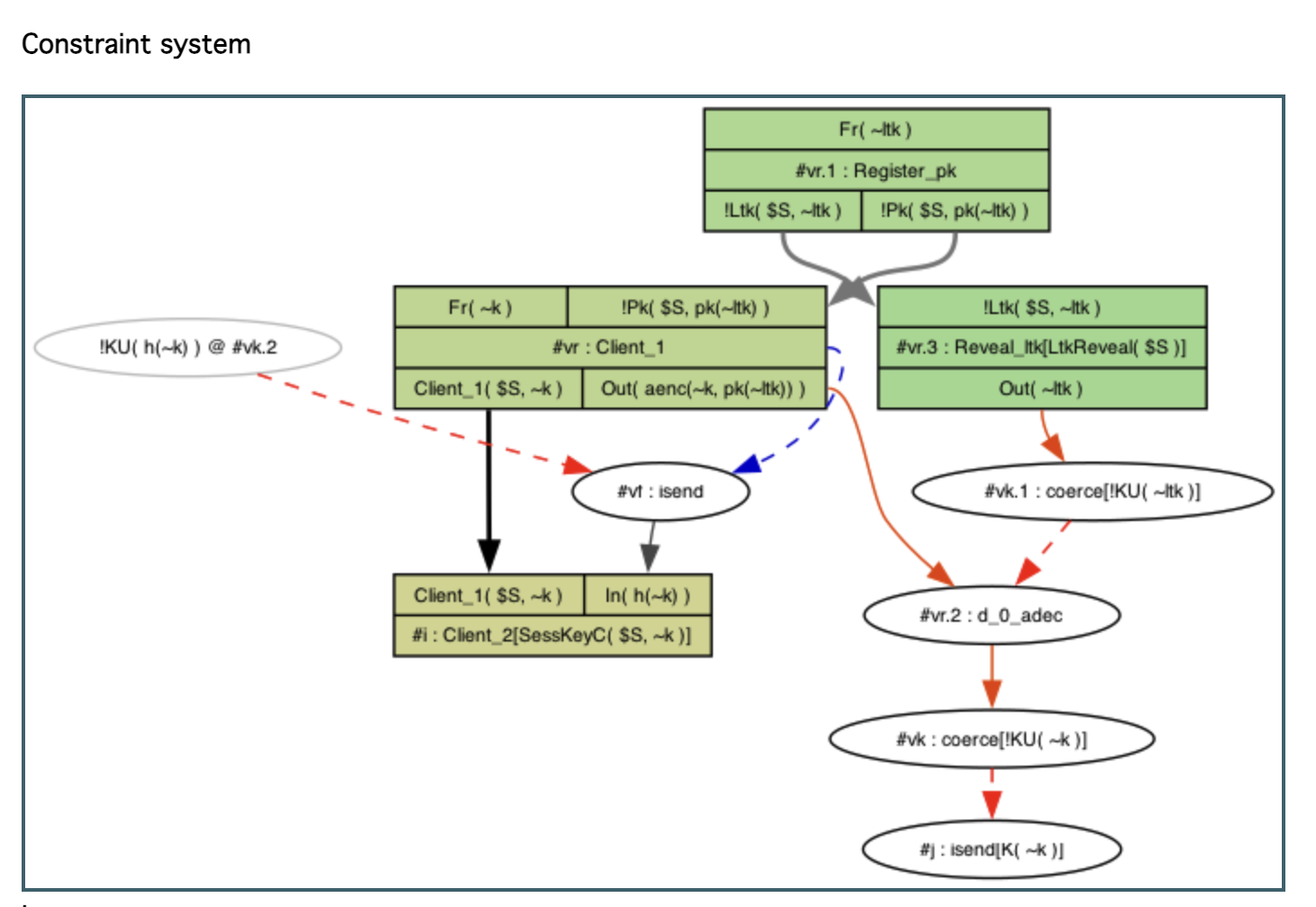
이 최종 상태에서 생성된 그래프(Constructed graph)가 모순(Contradiction)으로 이어지는데, 그 이유는 그래프에 LtkReveal(S)이 포함되어 있기 때문이다.
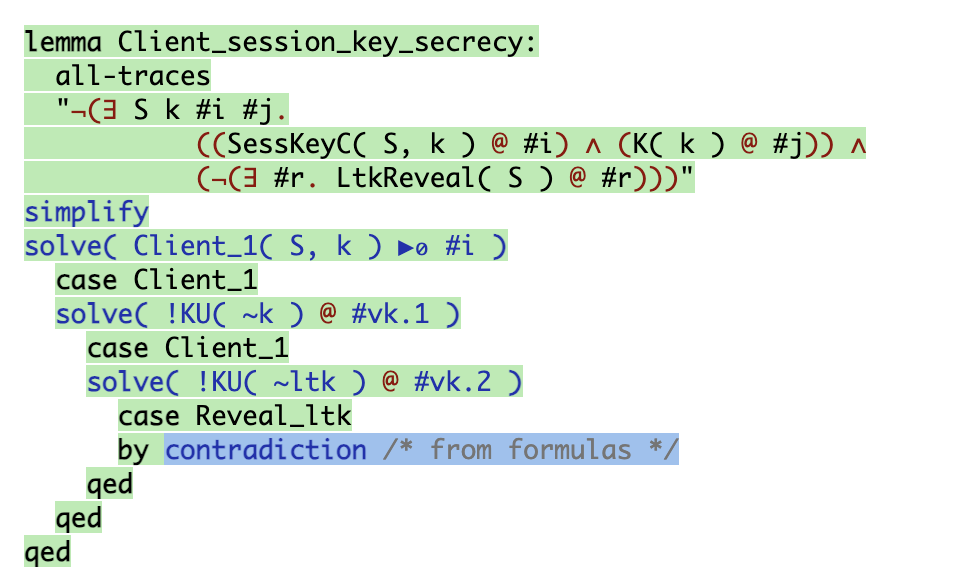
lemma는 이제 초록색으로 색칠되고 성공적으로 증명되었다는 것을 의미한다. 만약 반례를 찾았다면, 붉은색으로 칠해질 것이다.
Tamarin의 그래프에서는 다양한 종류의 화살표가 사용되며, 각각 다른 의미를 갖는다.
- 일반적인 검은색 또는 회색 실선(solid) 화살표는 프로토콜의 사실(facts)의 기원(origin)을 나타낸다.
- 붉은색 또는 주황색 실선은 공격자가 받은 메시지에서 값을 추출하는 과정을 나타낸다.
점선 화살표(Dashed arrows)의 경우 두 개의 액션 사이에 순서(ordering) 제약이 있음을 나타낸다.
- 검은색 점선 : 공식(formulas)에서 유도된 순서 제약 (lemma나 특정 restriction에서 유래)
- 진한 파란색 : 새로운(fresh) 값에서 유도된 순서 제약 (새로운 값은 반드시 그 값을 생성한 후에만 사용될 수 있음)
- 빨간색 점선 : 공격자가 값을 조합하는 과정에서 발생하는 단계
- 진한 주황색 점선 : Tamarin의 정규형 조건(normal form conditions)에서 유도된 순서 제약
- 보라색 점선 : 단사적 사실(Injective Fact)에서 기인한 순서 제약 (ex. 특정한 값이 한 번 만 사용될 수 있음)
초록색 점선 화살표는 Tamarin의 증명 과정에서 불완전한(adversary deduction) 추론 단계를 나타낸다. 즉, 공격자가 특정 값을 유추하는 과정에서 아직 완전히 증명되지 않은 단계를 시각적으로 표현할 때 사용된다.
그래프에서 약어(abbreviations) 사용 옵션을 사용하면 길거나 반복되는 항(term)들을 약어로 변환하여 표시할 수 있다.
