
📚 문제 설명
하드디스크는 한 번에 하나의 작업만 수행할 수 있습니다. 디스크 컨트롤러를 구현하는 방법은 여러 가지가 있습니다. 가장 일반적인 방법은 요청이 들어온 순서대로 처리하는 것입니다.
예를들어 다음와 같은 요청이 들어왔을 때를 그림으로 표현하면 아래와 같습니다.
0ms 시점에 3ms가 소요되는 A작업 요청
1ms 시점에 9ms가 소요되는 B작업 요청
2ms 시점에 6ms가 소요되는 C작업 요청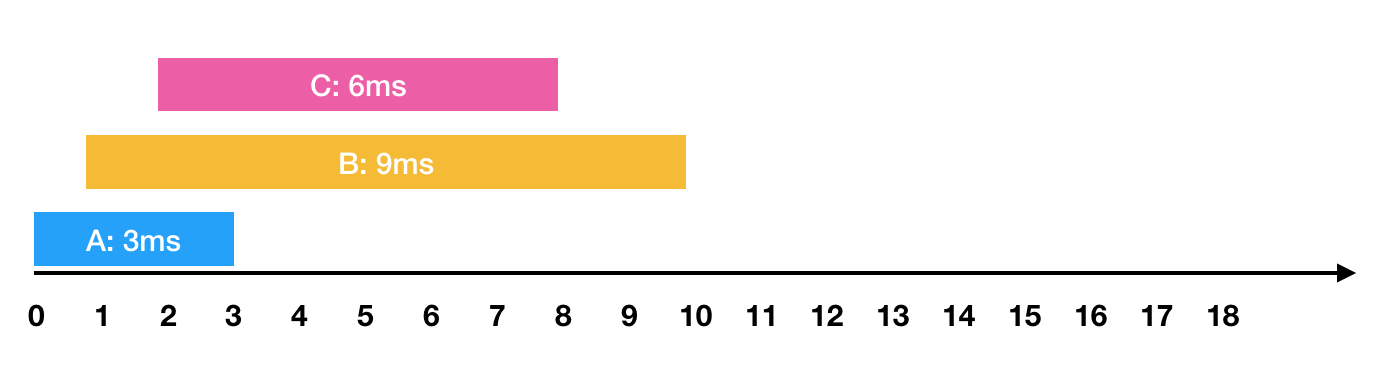
한 번에 하나의 요청만을 수행할 수 있기 때문에 각각의 작업을 요청받은 순서대로 처리하면 다음과 같이 처리 됩니다.
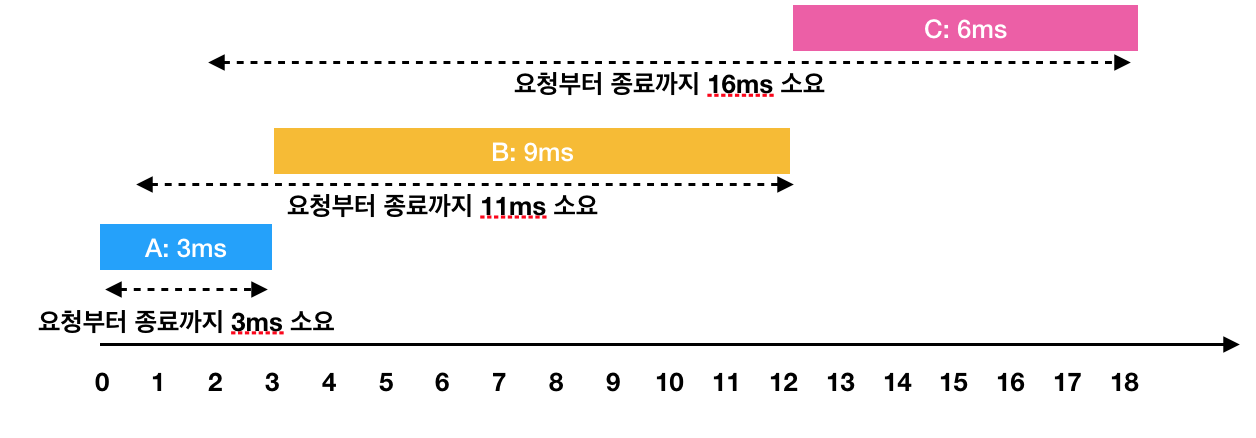
A: 3ms 시점에 작업 완료 (요청에서 종료까지 : 3ms)
B: 1ms부터 대기하다가, 3ms 시점에 작업을 시작해서 12ms 시점에 작업 완료(요청에서 종료까지 : 11ms)
C: 2ms부터 대기하다가, 12ms 시점에 작업을 시작해서 18ms 시점에 작업 완료(요청에서 종료까지 : 16ms)이 때 각 작업의 요청부터 종료까지 걸린 시간의 평균은 10ms(= (3 + 11 + 16) / 3)가 됩니다.
하지만 A → C → B 순서대로 처리하면
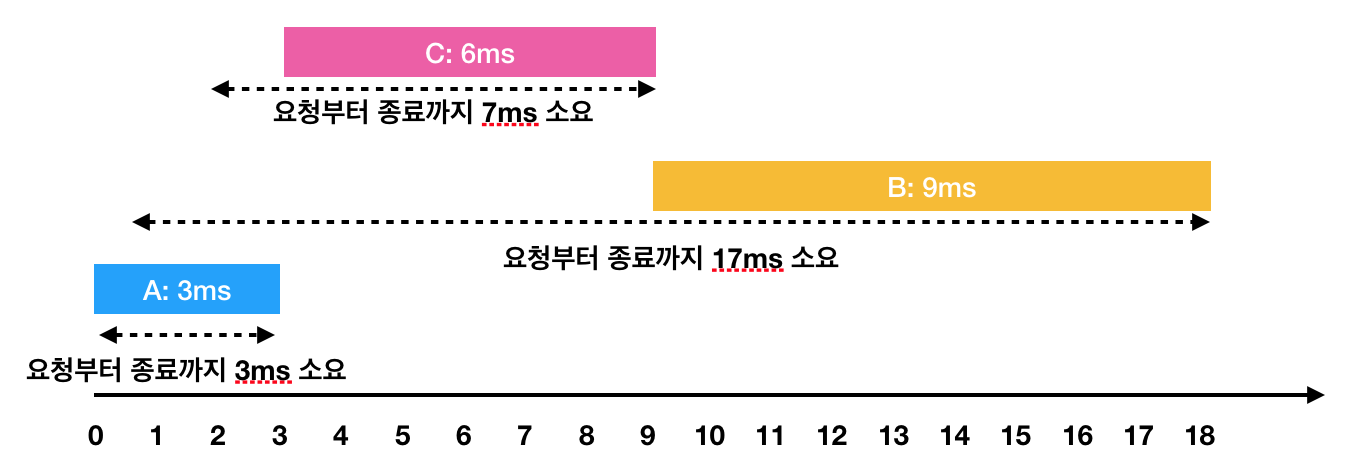
A: 3ms 시점에 작업 완료(요청에서 종료까지 : 3ms)
C: 2ms부터 대기하다가, 3ms 시점에 작업을 시작해서 9ms 시점에 작업 완료(요청에서 종료까지 : 7ms)
B: 1ms부터 대기하다가, 9ms 시점에 작업을 시작해서 18ms 시점에 작업 완료(요청에서 종료까지 : 17ms)이렇게 A → C → B의 순서로 처리하면 각 작업의 요청부터 종료까지 걸린 시간의 평균은 9ms(= (3 + 7 + 17) / 3)가 됩니다.
각 작업에 대해 [작업이 요청되는 시점, 작업의 소요시간]을 담은 2차원 배열 jobs가 매개변수로 주어질 때, 작업의 요청부터 종료까지 걸린 시간의 평균을 가장 줄이는 방법으로 처리하면 평균이 얼마가 되는지 return 하도록 solution 함수를 작성해주세요. (단, 소수점 이하의 수는 버립니다)
🔥 제한 조건
- jobs의 길이는 1 이상 500 이하입니다.
- jobs의 각 행은 하나의 작업에 대한 [작업이 요청되는 시점, 작업의 소요시간] 입니다.
- 각 작업에 대해 작업이 요청되는 시간은 0 이상 1,000 이하입니다.
- 각 작업에 대해 작업의 소요시간은 1 이상 1,000 이하입니다.
- 하드디스크가 작업을 수행하고 있지 않을 때에는 먼저 요청이 들어온 작업부터 처리합니다.
입출력 예
jobs return
[[0, 3], [1, 9], [2, 6]] 9📖 문제 풀이
Code_1 - 실행 에러
import heapq def solution(jobs): t, time = 0, [] # t : 현재까지 소요된 시간, time : 각 소요시간을 담은 list heapq.heapify(jobs) t = jobs[0][1] - jobs[0][0] time.append(t) heapq.heappop(jobs) while len(jobs) > 1: if jobs[0][0] <= t and jobs[1][0] <= t: if jobs[0][1] >= jobs[1][1]: b_t = jobs[0] jobs[0] = jobs[1] jobs[1] = b_t t += jobs[0][1] time.append(t-jobs[0][0]) heapq.heappop(jobs) else: t += jobs[0][1] time.append(t-jobs[0][0]) heapq.heappop(jobs) t += jobs[0][1] time.append(t-jobs[0][0]) return round(sum(time) / 3)1. 첫번째 작업 수행 종료 - 현재까지 소요된 시간 t 2. 2,3 번째 작업의 요청 시점이 t보다 작은 경우 - 2, 3번째 작업의 소요시간을 비교하여 더 작은 작업을 먼저 수행 3. 2,3 번째 작업의 요청 시점이 t보다 큰 경우 - 작업 요청 시점이 더 작은 작업을 먼저 수행 * 우선 작업 요청 시점을 기준으로 min heap으로 정렬 * 현재까지의 시점을 합하여 변수에 저장 * heapq의 최솟값(jobs[0])에 대해 소요시간 계산Code_2 - 성공
def solution(jobs): time, t, cnt, start = 0, 0, 0, -1 heap = [] while cnt < len(jobs): for job in jobs: if start < job[0] <= t: heapq.heappush(heap, (job[1], job[0])) if len(heap) > 0: cur = heapq.heappop(heap) start = t t += cur[0] time += (t - cur[1]) cnt += 1 else: t += 1 return int(time / len(jobs))
- heap을 별도로 생성하여 (작업 소요시간, 요청 시점) 형식으로 정렬
