
📚 문제 설명
n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.
다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.
🔥 제한 조건
- 섬의 개수 n은 1 이상 100 이하입니다.
- costs의 길이는 ((n-1) * n) / 2이하입니다.
- 임의의 i에 대해, costs[i][0] 와 costs[i][1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i][2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
- 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
- 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
- 연결할 수 없는 섬은 주어지지 않습니다.
입출력 예
n costs return
4 [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] 4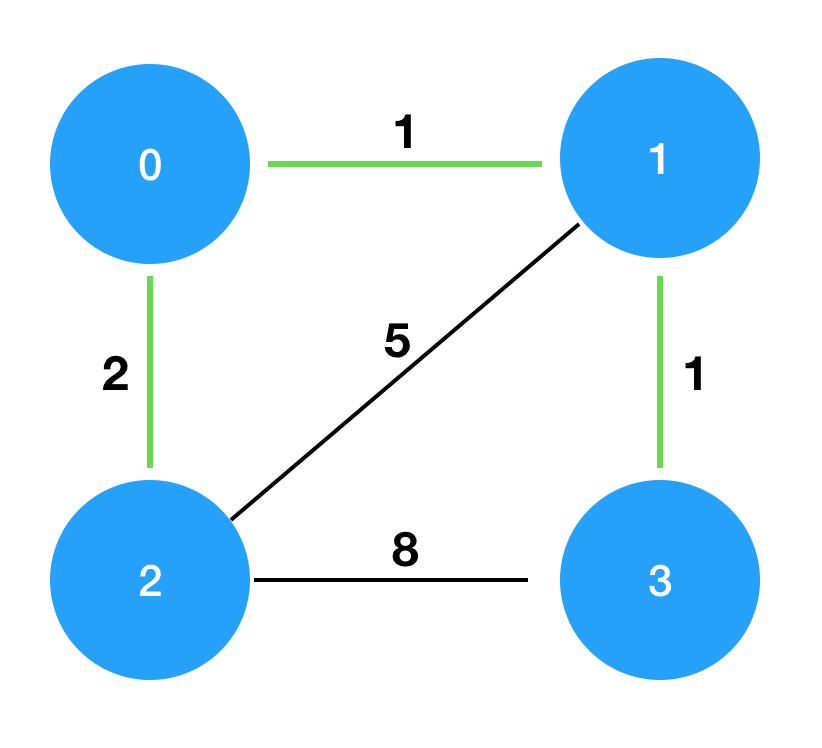
📖 문제 풀이
Code_1 - 실행 에러
import heapq def solution(n, costs): answer = 0 INF = int(1e9) graph = [[] for _ in range(n)] distance = [INF]*n for c in costs: node, target, cost = c graph[node].append((target, cost)) def dijkstra(start): q = [] heapq.heappush(q, (0, start)) distance[start] = 0 while q: cost, node = heapq.heappop(q) if distance[node] < cost: continue for next_g in graph[node]: next_cost = next_g[1] + cost if next_cost < distance[next_g[0]]: distance[next_g[0]] = next_cost heapq.heappush(q, (next_cost, next_g[0])) dijkstra(0) print(distance) return answer
- 다익스트라 알고리즘으로 구현하려고 노력했지만 답이 안 나올것 같아서 결국 구글링으로 힌트를 얻음...
Code_2 - 성공
def solution(n, costs): answer = 0 costs.sort(key=lambda x: x[2]) connect = set([costs[0][0]]) # 시작 연결점 while len(connect) != n: for cost in costs: # print(cost[0], cost[1], connect, answer) if cost[0] in connect and cost[1] in connect: continue if cost[0] in connect or cost[1] in connect: connect.update([cost[0], cost[1]]) answer += cost[2] break return answer
- 건설 비용을 기준으로 오름차순 정렬하여 비용이 가장 낮은 조건들을 먼저 연산함
- set안에 모든 위치가 연결될 때까지 반복문을 수행하며 두섬이 이미 연결된 경우 무시하고 연결되지 않은 경우 비용을 더함
- set.update()를 통해 중복을 제거함
