목적
학교 자료구조 과목 수행으로 비선형 자료구조에 관해 블로그를 작성해야 되서 알아보게 되었다.
비선형 자료구조란?
비선형 자료구조는 데이터가 일렬로 나열되지 않고, 자료 간의 복잡한 관계를 표현할 수 있는 구조이다.
하나의 자료가 여러 자료와 연결될 수 있으며 대표적으로 트리와 그래프가 있다.
이 중 먼저 트리에 대해 알아볼 것이다.
트리
트리 (Tree)란 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조이다.
트리는 또한 트리 내에 다른 하위 트리가 있고 그 하위 트리 안에는 또 다른 하위 트리가 있는 재귀적 자료구조이기도 한다.
트리의 용어
트리의 용어로는
- 노드(node) : 트리의 구성요소
- 루트(root) : 부모가 없는 노드
- 서브트리(subtree) : 하나의 노드와 그 노드들의 자손들로 이루어진 트리
- 단말노드 : 자식이 없는 노드
- 비단말노드 : 적어도 하나의 자식을 가지는 노드
- 레벨(level) : 트리의 각층의 번호
- 높이(height) : 트리의 최대 레벨
- 차수(degree) : 노드가 가지고 있는 자식 노드의 개수
트리의 종류
1) 이진트리
모든 노드가 2개의 서브트리를 가지고 있는 트리이다.
- 이진 트리의 노드에는 최대 2개까지의 자식 노드가 존재한다.
- 모든 노드의 차수가 2 이하가 된다.
- 이진 트리에는 서브 트리간의 순서가 존재한다.
이진트리의 분류
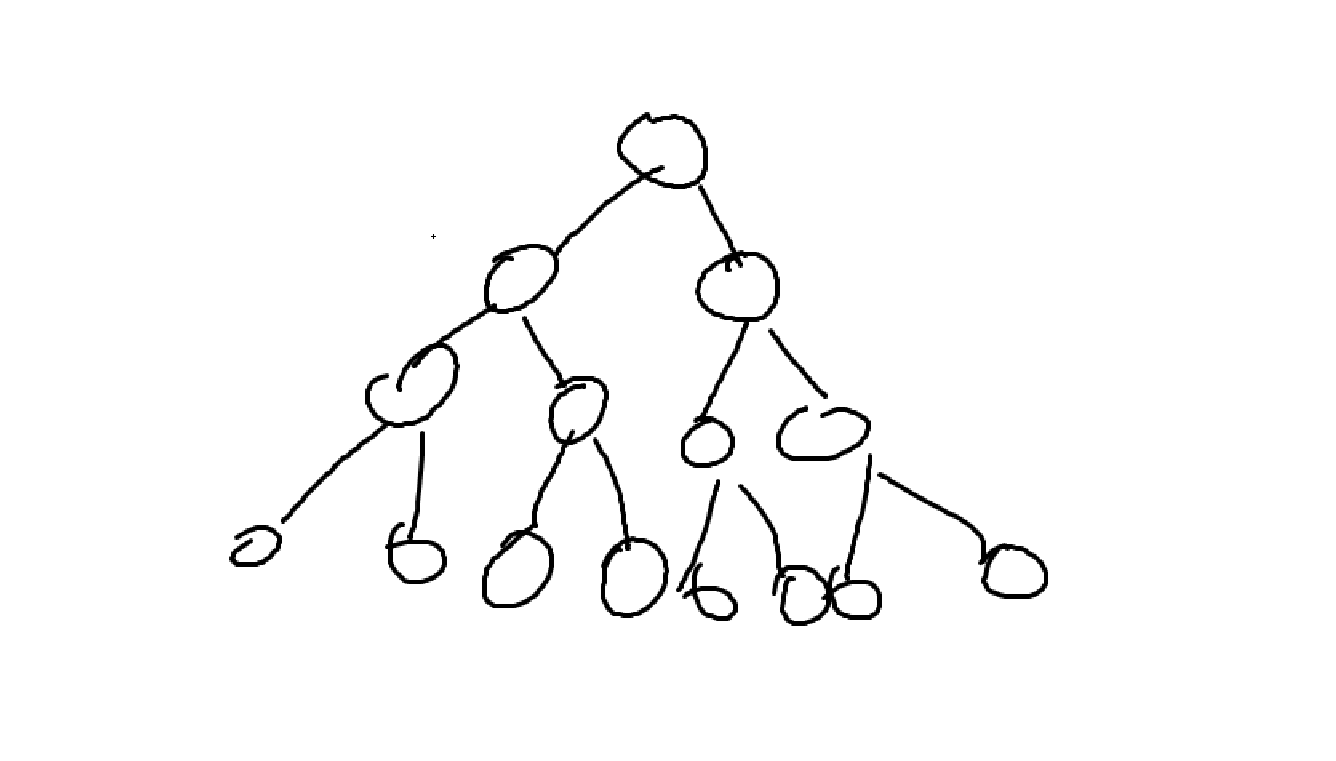
- 포화 이진트리 : 꽉찬 이진트리
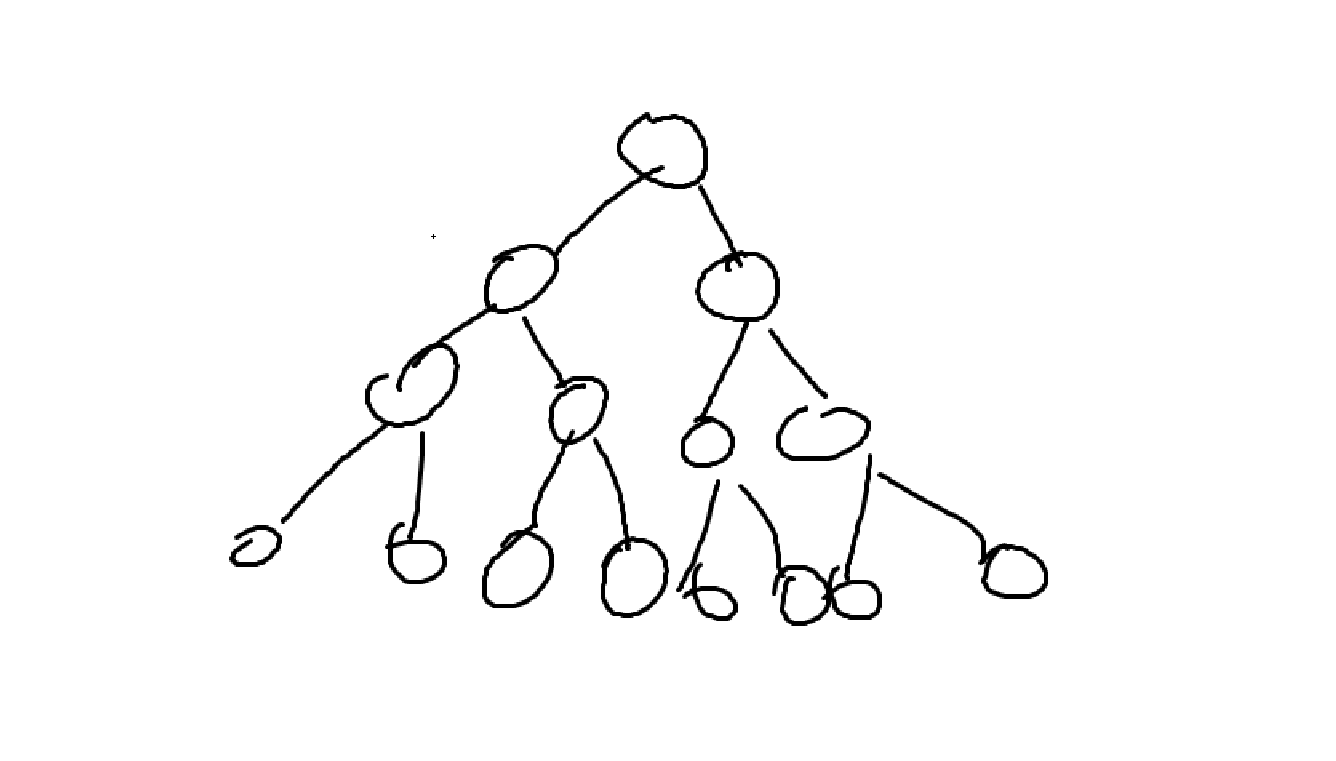
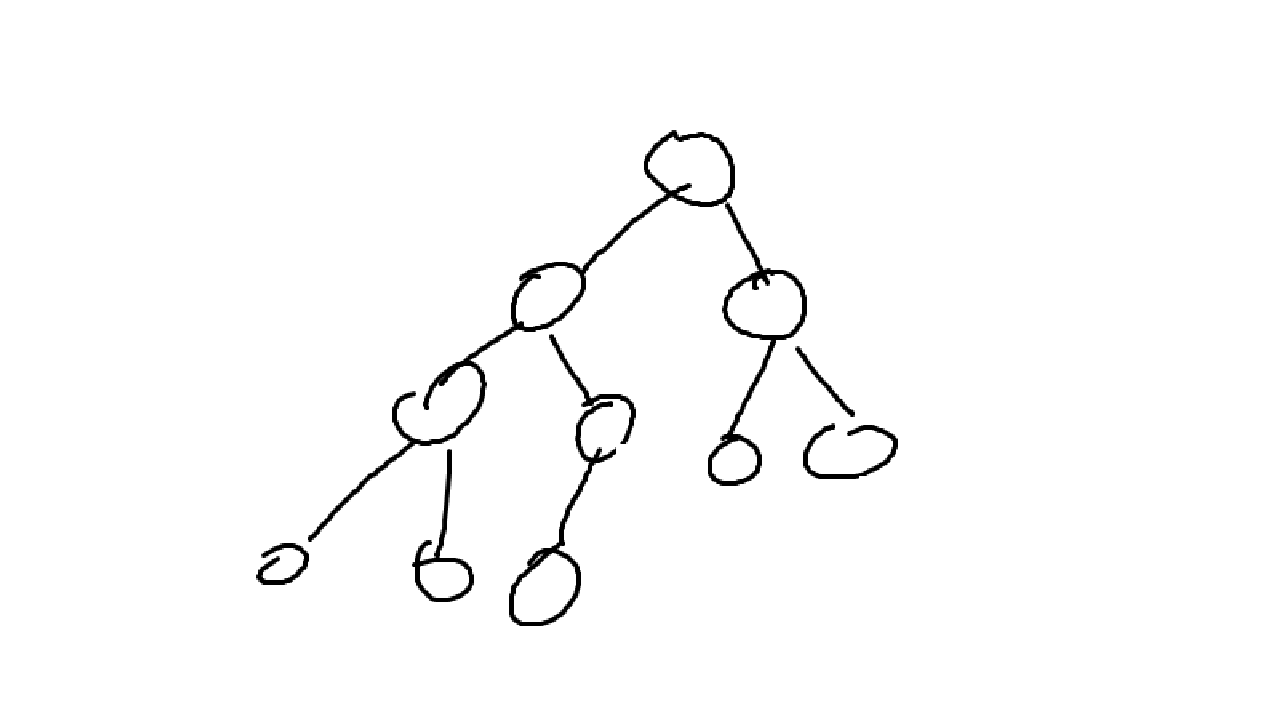
- 완전 이진트리 : 레벨 1부터 k-1까지는 노드가 모두 채워져 있고 마지막 레벨 k에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진트리
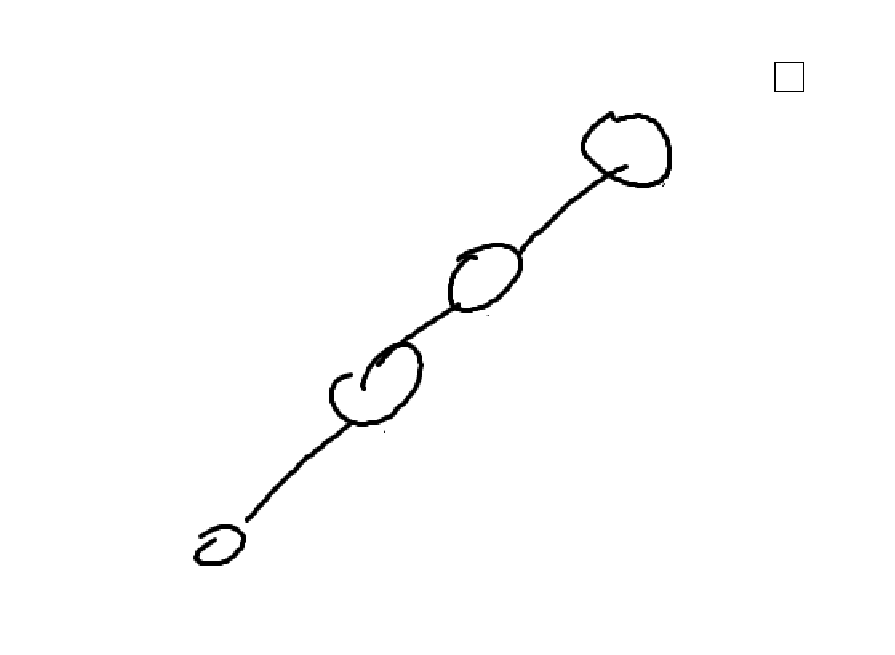
- 편향 이진 트리 : 최소 개수의 노드 개수를 가지며 왼쪽 혹은 오른 쪽의 서브 트리만을 가진 트리
2) 이진 탐색 트리
이진 탐색 트리는 자신보다 작은 값은 왼쪽 서브트리에, 자신보다 큰 값은 오른쪽 서브트리에 저장한다.
key(왼쪽 서브트리) ≤ key(루트노드) ≤ key(오른쪽 서브트리) 이다.
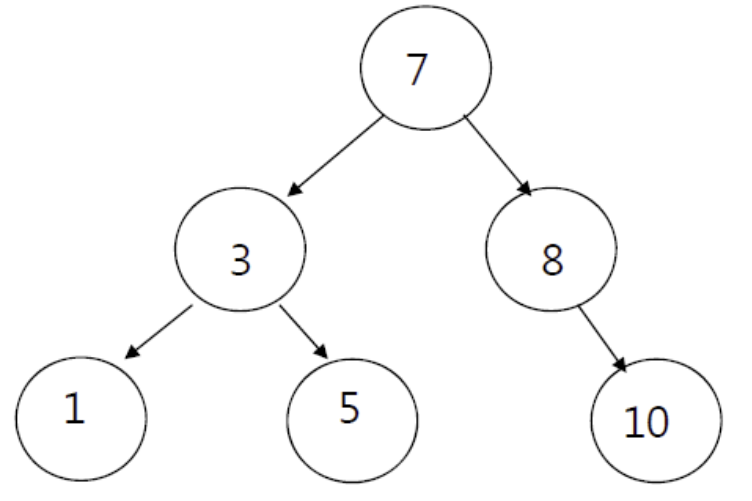
트리 탐색 기법
깊이 우선 탐색 - DFS (스택)
한 방향으로 갈 수 있을 때까지 가다가 더 이상 갈 수 없게 되면 돌아오는 방식이다.
1) 전위 순회
루트 -> 왼쪽 서브트리 -> 오른쪽 서브트리 순으로 방문한다.
void preorder(Node* root) {
if (root == NULL) return; // 탐색할 노드가 없으면 빠져 나옴
printf("%c ", root->data); // 데이터 출력
preorder(root->left); // 왼쪽 노드 탐색
preorder(root->right); // 오른쪽 노드 탐색
}2) 중위 순회
왼쪽 서브트리 -> 루트 -> 오른쪽 서브트리 순으로 방문한다.
void inorder(Node* root) {
if (root == NULL) return; // 탐색할 노드가 없으면 빠져 나옴
inorder(root->left); // 왼쪽 노드 탐색
printf("%c ", root->data); // 데이터 출력
inorder(root->right); // 오른쪽 노드 탐색
}3) 후위 순회
왼쪽 서브트리 -> 오른쪽 서브트리 -> 루트 순으로 방문한다.
void postorder(Node* root) {
if (root == NULL) return; // 탐색할 노드가 없으면 빠져 나옴
postorder(root->left); // 왼쪽 노드 탐색
postorder(root->right); // 오른쪽 노드 탐색
printf("%c ", root->data); // 데이터 출력
}너비 우선 탐색 - BFS (큐)
BFS는 레벨 순회와 같은 방식으로 한 레벨에 있는 노드를 모두 방문한 후 다음 레벨로 내려가 탐색을 계속하는 방식이다.
void bfs(int start) {
queue[rear++] = start; // 시작 노드를 큐에 삽입
visited[start] = 1; // 시작 노드 방문 표시
while (front < rear) { // 큐가 비어있지 않으면 반복
int node = queue[front++]; // 큐에서 노드 하나 꺼냄
printf("%d ", node); // 꺼낸 노드 출력
for (int i = 0; i < n; i++) { // 모든 노드를 확인
if (graph[node][i] && !visited[i]) { // 인접하고 아직 방문 안했으면
queue[rear++] = i; // 큐에 추가
visited[i] = 1; // 방문 표시
}
}
}
}코드
#include <stdio.h>
#include <stdlib.h>
// 트리 노드 구조체 정의
typedef struct Node {
char data;
struct Node* left;
struct Node* right;
} Node;
// 새 노드 생성 함수
Node* createNode(char data) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->data = data;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
// 전위 순회
void preorder(Node* root) {
if (root == NULL) return;
printf("%c ", root->data);
preorder(root->left);
preorder(root->right);
}
// 중위 순회
void inorder(Node* root) {
if (root == NULL) return;
inorder(root->left);
printf("%c ", root->data);
inorder(root->right);
}
// 후위 순회
void postorder(Node* root) {
if (root == NULL) return;
postorder(root->left);
postorder(root->right);
printf("%c ", root->data);
}
int main() {
Node* A = createNode('A');
Node* B = createNode('B');
Node* C = createNode('C');
Node* D = createNode('D');
Node* E = createNode('E');
A->left = B;
A->right = C;
B->left = D;
B->right = E;
printf("전위 순회 : ");
preorder(A);
printf("\n");
printf("중위 순회 : ");
inorder(A);
printf("\n");
printf("후위 순회 : ");
postorder(A);
printf("\n");
return 0;
}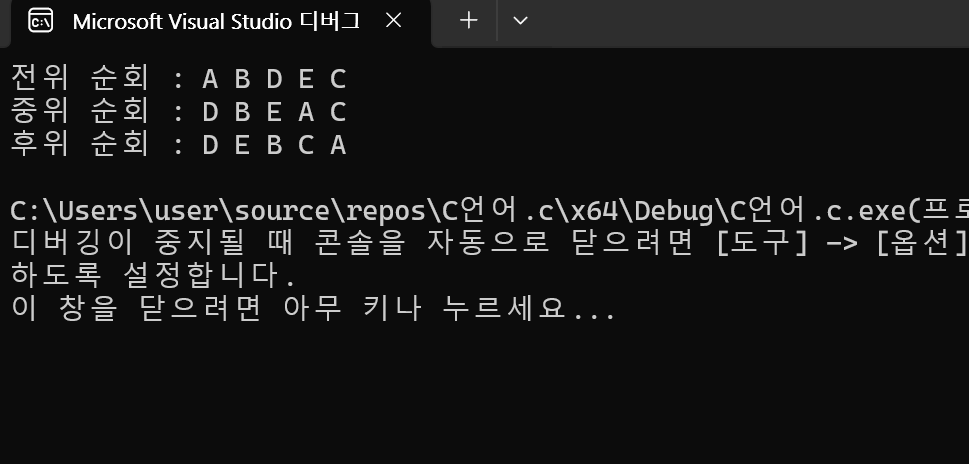
이런식으로 구현할 수 있다.
그래프
그래프란 정점과 간선으로 구성된 자료구조로, 객체 간의 복잡한 관계를 표현하고 분석하는데 사용된다.
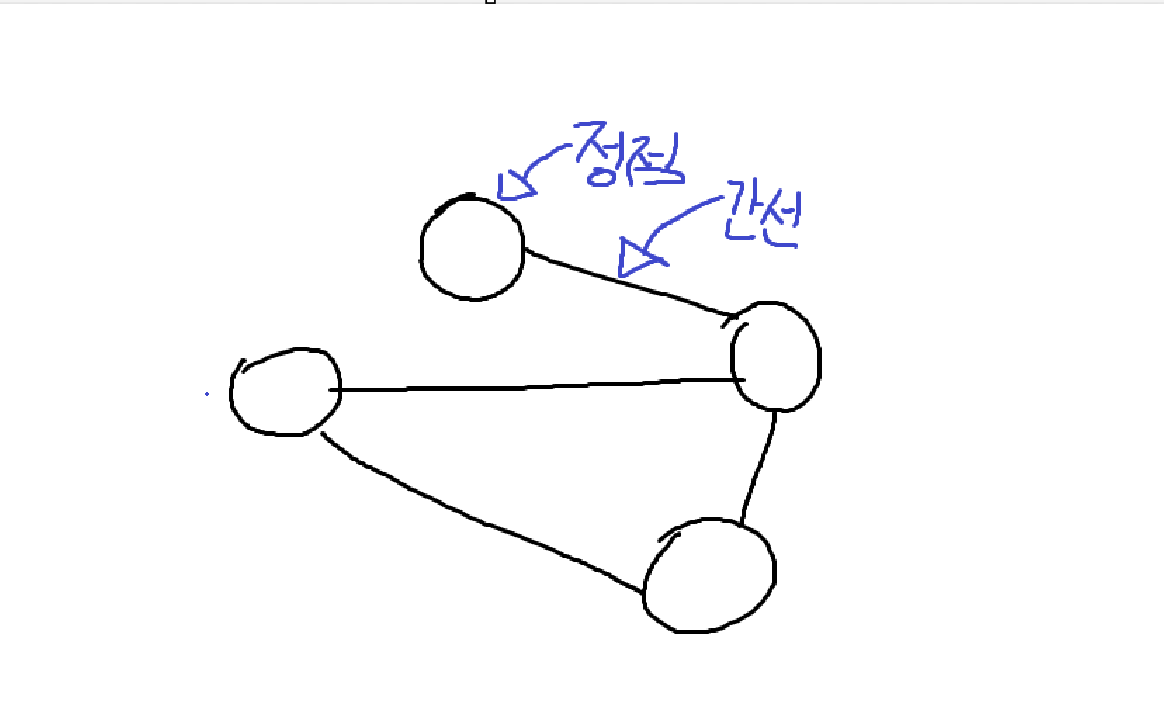
용어
- 정점 : 그래프를 구성하는 기본 단위로 객체나 개체를 나타낸다.
- 간선 : 두 정점을 연결하는 선으로 객체 간의 관계나 연결을 나타낸다.
그래프의 종류
무방향 그래프
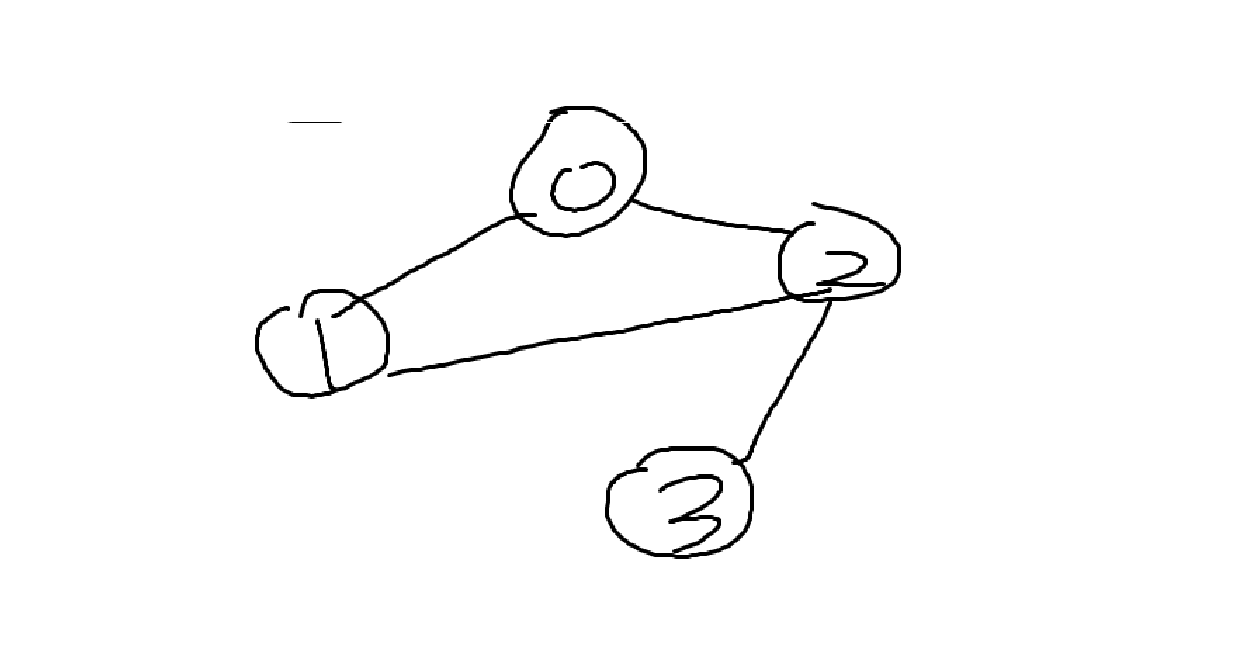
간선에 방향이 없는 그래프이다.
두 정점 사이가 양방향으로 연결되어 있다.
- 나타낼 때 소괄호()로 묶어 표시한다.
- (0,1)과 (1.0)은 같은 간선이다.
예시) E(G) = {(0,1),(0,2),(1,0),(2,0)}
방향 그래프
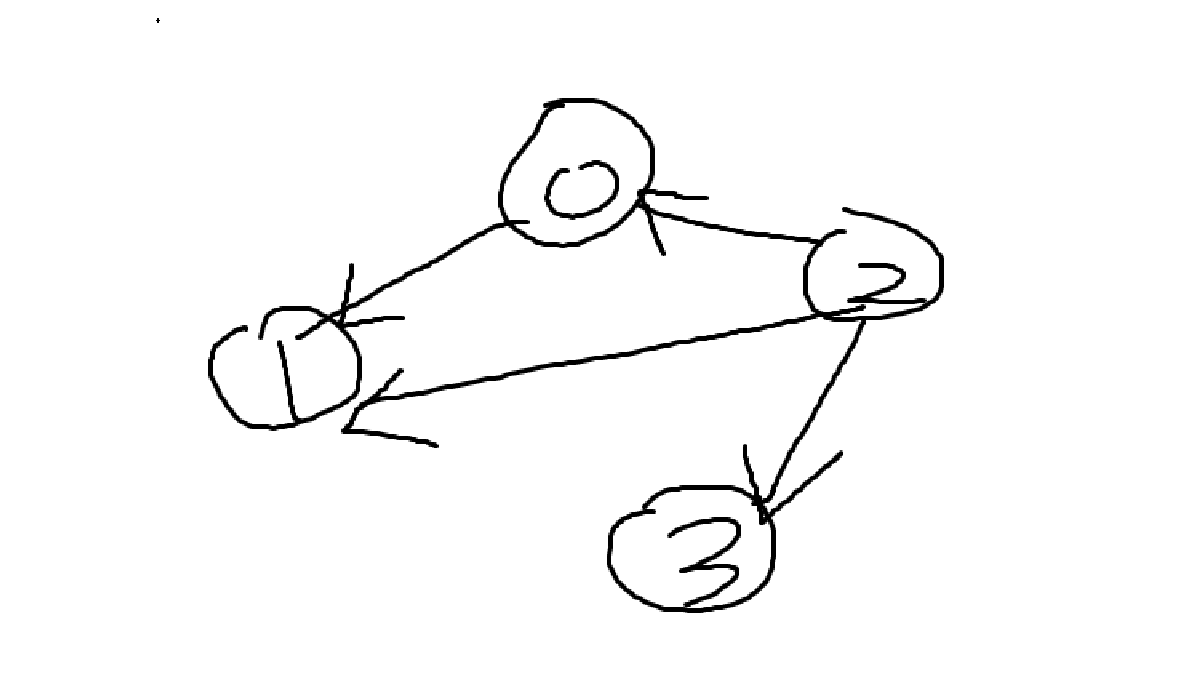
간선에 방향이 있는 그래프이다.
- <> 꺽쇠로 묶어 표시한다.
- <0,1>과 <1,0>은 다른 간선이다.
예시) E(G) = {<0,1>,<0,2>,<1,0>,<2,0>}
그래프 표현 방식
인접 행렬
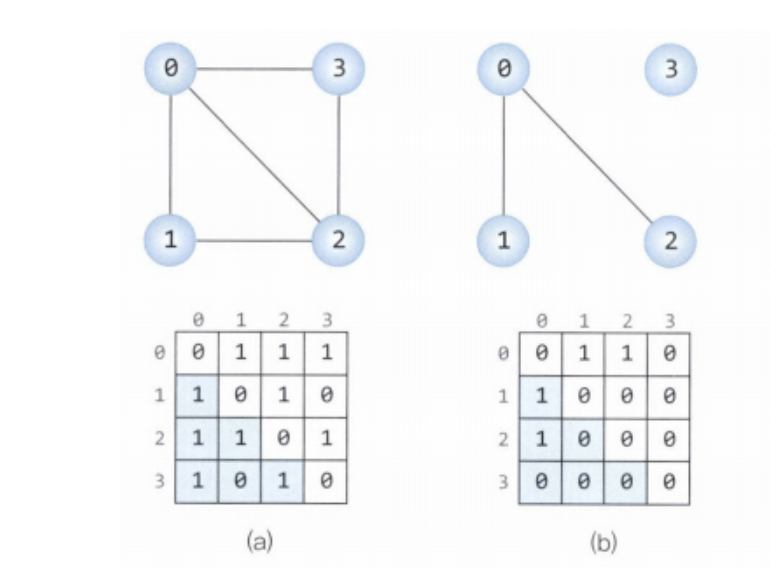
인접 행렬은 두 정점의 간선의 유무를 이중 배열 형태로 저장하게 된다.
무방향 그래프
양방향 구조로 0-1이 연결되어 있으면 1-0도 연결되어야 한다.
방향 그래프
한 쪽 방향으로만 연결되어 있어 0->1은 연결되어 있지만 1->0은 연결되어 있지 않을 수 있다.
인접 리스트
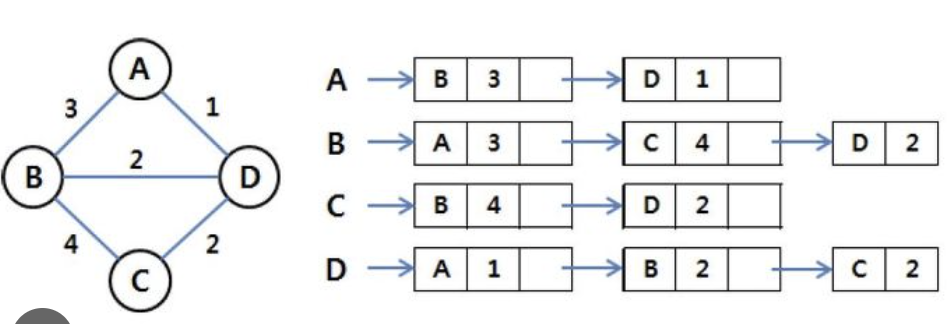
인접 리스트는 두 정점의 간선의 유무를 연결 리스트로 저장한다.
어느 정점과 연결되어 있는지만 저장한다.
그래프 탐색
DFS
한 방향으로 갈 수 있을 때까지 간다.
갈 수 없게 되면 가장 가까운 갈림길로 돌아가는 순회 방법이다.
인접 행렬로 나타내면 이렇게 구현할 수 있다.
void dfs(int v) {
visited[v] = 1; // 현재 노드 방문 표시
printf("%d ", v); // 방문한 노드 출력
for (int i = 0; i < MAX; i++) {
if (graph[v][i] && !visited[i]) { // i노드가 현재 노드와 연결되어 있고 방문하지 않았는지 확인
dfs(i); // 그렇다면 깊이 들어감
}
}
}BFS
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨여져 있는 정점을 나중에 방문하는 순회 방법이다.
인접 행렬로 나타내면 이렇게 구현할 수 있다.
void bfs(int start) {
int queue[MAX];
int front = 0, rear = 0;
visited[start] = 1; // 시작 노드 방문 표시
queue[rear++] = start; // 큐에 시작 노드 삽입
while (front < rear) { // 큐가 빌때까지
int v = queue[front++]; // 큐에서 하나씩 꺼냄
printf("%d ", v); // 방문한 노드 출력
for (int i = 0; i < MAX; i++) {
if (graph[v][i] && !visited[i]) { // 연결되어 있고 방문하지 않은 노드인지 확인
visited[i] = 1; // 방문 표시
queue[rear++] = i; // 큐에 추가
}
}
}
}
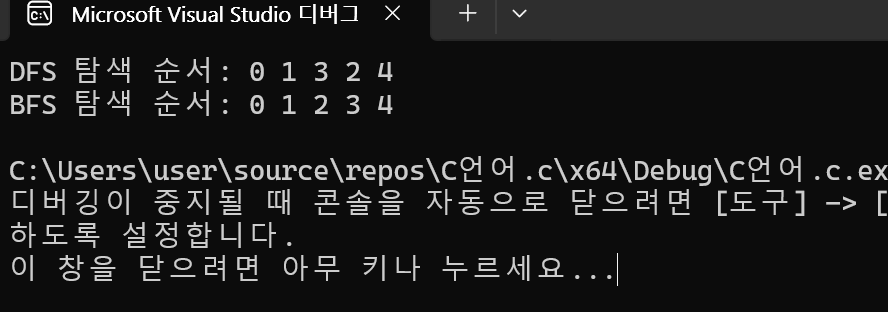
전체 코드
전체 코드로 구현하면 이렇게 나타낼 수 있다.
#include <stdio.h>
#define MAX 5
int graph[MAX][MAX] = {
// 0 1 2 3 4
{0, 1, 1, 0, 0},
{1, 0, 0, 1, 0},
{1, 0, 0, 1, 1},
{0, 1, 1, 0, 1},
{0, 0, 1, 1, 0}
};
int visited[MAX];
// DFS
void dfs(int v) {
visited[v] = 1;
printf("%d ", v);
for (int i = 0; i < MAX; i++) {
if (graph[v][i] && !visited[i]) {
dfs(i);
}
}
}
// BFS
void bfs(int start) {
int queue[MAX];
int front = 0, rear = 0;
visited[start] = 1;
queue[rear++] = start;
while (front < rear) {
int v = queue[front++];
printf("%d ", v);
for (int i = 0; i < MAX; i++) {
if (graph[v][i] && !visited[i]) {
visited[i] = 1;
queue[rear++] = i;
}
}
}
}
int main() {
printf("DFS 탐색 순서: ");
for (int i = 0; i < MAX; i++) visited[i] = 0; // 초기화
dfs(0);
printf("\n");
printf("BFS 탐색 순서: ");
for (int i = 0; i < MAX; i++) visited[i] = 0; // 초기화
bfs(0);
printf("\n");
return 0;
}
마무리
이상으로 비선형 자료구조의 트리와, 그래프에 대해 알아보았다.