에라토스테네스의 채는 아주 유명한 소수판별법입니다
효율이 좋아서그럼
만약 어떤 수가 소수다?
그럼 그 수의 배수들은 소수가 아니겠죠?
예를 들면 2는 소수잖아요
근데 이제 4, 6, 8은 소수가 아닌거임
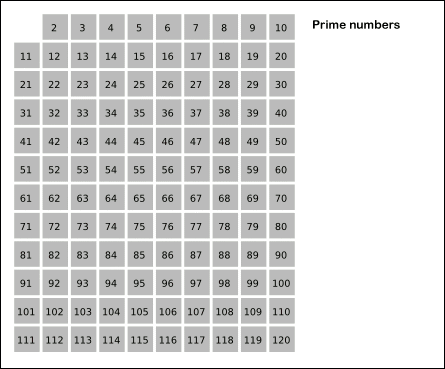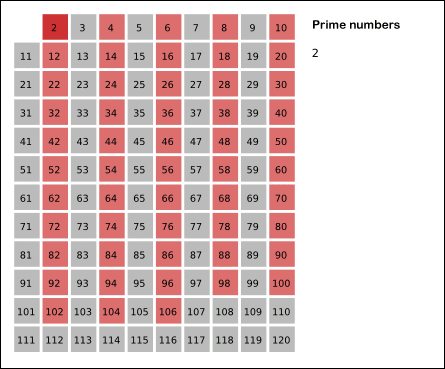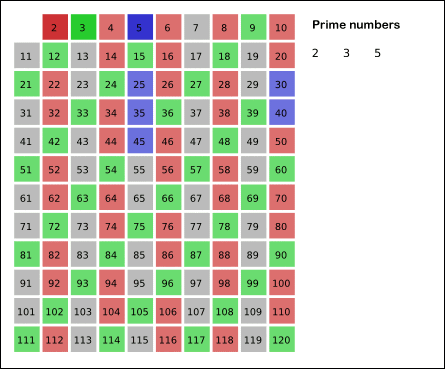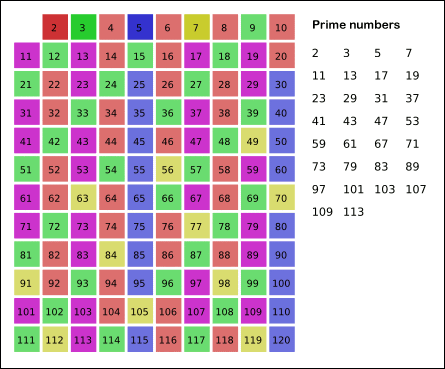
이런식으로 소수 하나 저당잡은 다음에 그 수의 배수들은 전부 다 합성수다 이거죠 이렇게 후다닥 소수를 구하면 빠르대요
아마 메모이제이션같은 느낌이 아닐까 합니다
def prime_list(n):
# 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
sieve = [True] * n
# n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
m = int(n ** 0.5)
for i in range(2, m + 1):
if sieve[i] == True: # i가 소수인 경우
for j in range(i+i, n, i): # i이후 i의 배수들을 False 판정
sieve[j] = False
# 소수 목록 산출
return [i for i in range(2, n) if sieve[i] == True]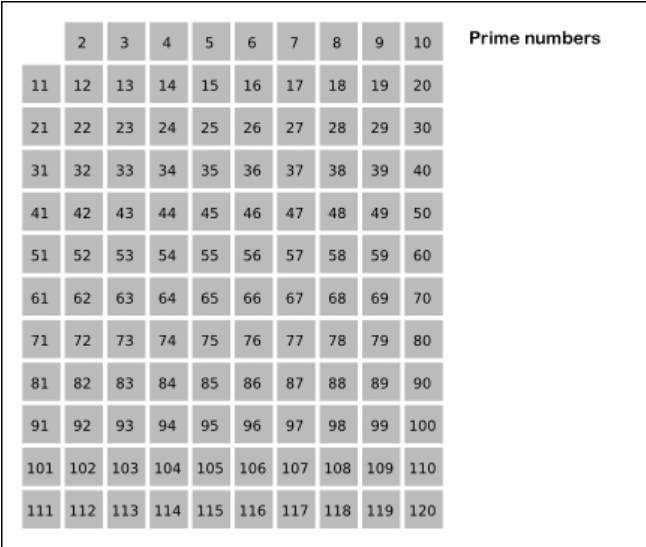
에라토스테네스의 채가 아니라 에라토스테네스의 '체'로 고쳐주셨으면 해요.