[프로그래머스] 억억단을 외우자★ - 접근과 풀이(Python) with 조화급수의 시간복잡도

지누·2024년 7월 14일

알고리즘을 어느정도 오래 했고, 실제 기업에서 진행하는 코테에 미리 적응하기 위해 요즘은 백준이 아닌 프로그래머스에서 알고리즘 스터디를 진행중이다.
백준과 VSCode 환경에 적응하다가, 자동완성도 없고 불친절한 에러메세지를 띄워주는 웹IDE를 사용하려니 너무 힘들었다. 그치만 불편한 환경에 적응하려고 한다.

레벨 1~5까지 있는데, 레벨 2에서 턱턱 막히고, 레벨3는 정말 어렵다.. 체감 난이도가 골드 상위권쯤 되는 것 같다. vscode 자동완성에 찌들어서라고 굳게 믿고싶다..^^

문제 : https://school.programmers.co.kr/learn/courses/30/lessons/138475

문제에는 억억단이라고 되어있는데, 최악의 테스트케이스를 생각해 보았을 때 1 ~ 500만까지 모든 숫자의 약수의 개수를 구하는 것이 핵심이다.
그리고, 그 약수의 개수를 가지고 [s,e] 구간에서의 최댓값을 구하는 것 또한 2번째 핵심이었는데, 이 부분은 전혀 생각하지 못하고 정답을 참고했다.

접근 1. 약수의 개수 구하기

약수의 개수를 구하는 것과, 소수 판별 등은 PS의 정수론 분야 단골 손님이다. 난이도도 적당히 어려워서 코테에서 나올 법 한데, 구현, 그리디 같은 장르를 열심히 풀다 보니 감을 못잡았다.

1.1. 약수의 개수 구하기 - 방법 1, $O(e\sqrt{e})$

내가 시도했던 방법이다.
1부터 $e$ 까지의 숫자 num에 대해, 1부터 $\sqrt{e}$ 까지 나누어 떨어지는 지 판별하여 num의 약수의 개수를 일일이 구하는 방법이다.

위 방법은 $O(e)*O(\sqrt{e})$ = $O(e\sqrt{e})$ 의 시간 복잡도를 가진다.
e가 500만이므로, 1억이 넘어가므로 TLE가 날 것이라 예상은 했는데, 프로그래머스는 시간 제한을 명시하지 않아서 될지도 모른다고 생각하고 시도했지만 어림 없었다.

아래는 약수 개수를 구하는 부분의 코드이다.

import math
MAX = 5_000_001
def solution(e, starts):
    cnt = [0]*(e+1)
    for num in range(1,e+1):
        for div in range(1,int(math.sqrt(num))+1):
            if num % div == 0:
                cnt[num]+=2
            if div**2==num:
                cnt[num]-=1

1.2. 약수의 개수 구하기 - 방법 2, $O(e\log{e})$ with 조화수열

다른 사람의 풀이를 참고한 부분이다.
1부터 $e$ 까지의 숫자 num에 대해, num*2, num*3, num*4, ...를 $e$ 까지 진행하여 num*k에 해당하는 count를 1씩 더해주는 방법이다.

1*1, 1*2, 1*3, 1*4 ... 1*500만
2*1, 2*2, 2*3, 2*4 ... 2*250만
3*1, 3*2, 3*3, 3*4 ... 3*167만
...
10000*1, 10000*2, 10000*3, 10000*4 ... 10000*500
...
500만*1

이런식으로 진행된다. 1을 인수로 가지는 모든 수를 찾고, 2,3,4,5...500만을 인수로 가지는 모든 수를 찾는 방법이라는 것이 직관적으로 보인다.

위 방법의 시간복잡도는 조화수열에 근사한 $O(e\log{e})$ 이다.

조화수열

첫 번째 행은 500만개, 두 번째 행은 250만개, 3번째 행은 167만개... 이렇게 계산된다.
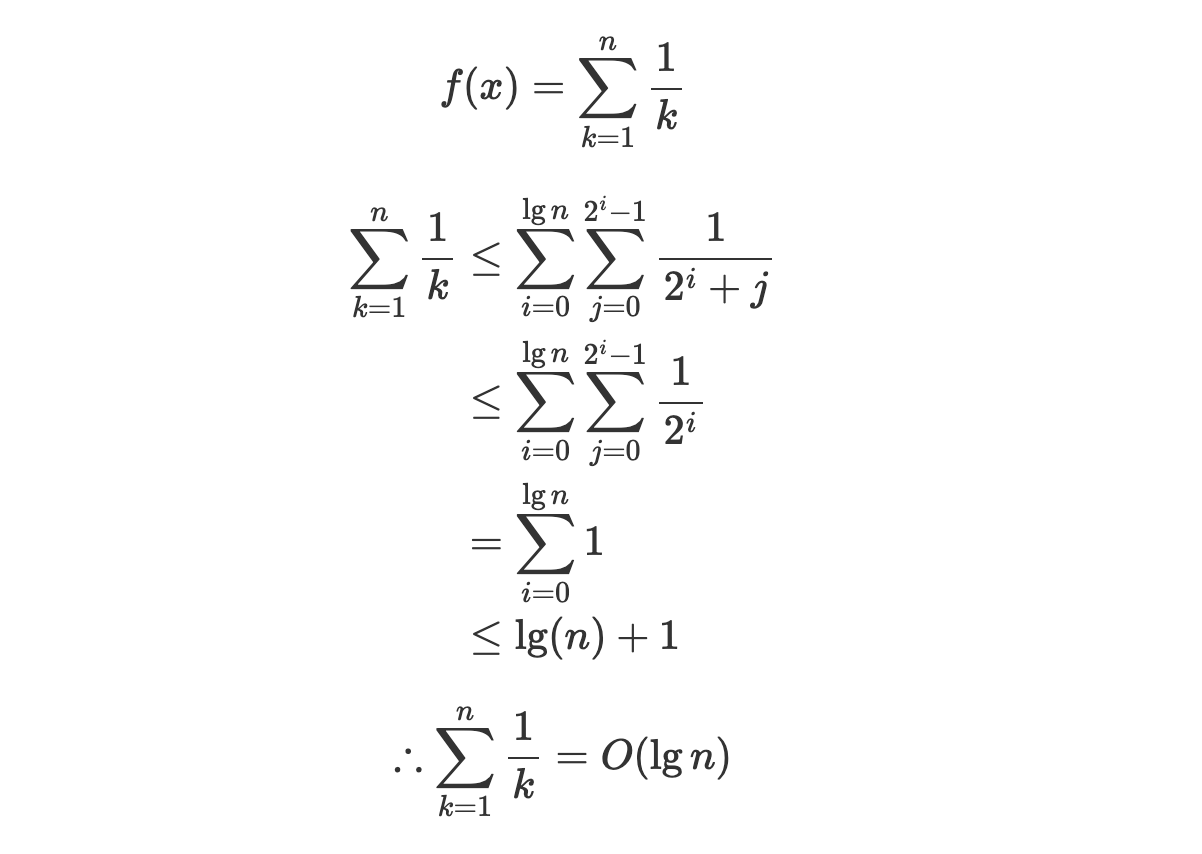
즉 최대 범위 ${e}$ 에 대해 $O(\frac{e}{1} + \frac{e}{2} + \frac{e}{3} + ... \frac{e}{e})$ = $O(e)*O(\sum_{i=1}^{e} \frac{1}{i})$ $\approx$ $O(e\log{e})$ 이다.

위와 같은 과정을 통해 얻어지며, 자세한 과정이 궁금하다면 검색을 통해 알아보는 것을 권유한다.

e가 500만이라는 것을 보았을 때, $O(e\log{e})$ 의 시간 복잡도를 바로 떠올렸어야 하는데, 위의 방식이 $O(e\log{e})$ 시간 복잡도를 가지는지 몰랐다. 자주 나오는 코드는 아니지만 알아두면 좋을 것 같다. 아래는 풀이 코드이다.

## 약수의 개수 구하기 방법 2
import math
MAX = 5_000_001
def solution(e, starts):
    cnt = [1]*(e+1)
    for num in range(1,e+1):
        for increment in range(num*2,e+1,num):
            cnt[increment]+=1

접근 2. 구간 내 최댓값 구하기

cnt[e] 배열에 1부터 e까지의 약수의 개수를 넣어 놓았다.

그리고 [s,e]의 범위에 대해서 최댓값의 인덱스를 정답으로 반환해야 한다.
그리고 e는 고정되어 있으며 s의 범위가 $1\leq s \leq e$ 이다. 그리고 해당 s를 최대 10만개 제공해주므로, $O(10만*500만)$ 이다. 정상적인 방법으로 $O(se)$ 의 시간 복잡도로 접근했더니 당연히 TLE가 났는데, 이 부분도 놓치고 있었다.

e가 고정되어 있다는 점을 활용하여 뒤에서부터 접근하는 dp를 사용하면 된다.
본 게시글에서는 조화수열의 시간복잡도를 알아보는 것이 메인이었기에, 내가 실패한 코드와 성공한 코드만 적겠다.

# 접근 2. 실패한 코드 O(se)
answer=[]
    for start in starts:
        ansVal=-1
        ansIdx=-1
        for idx in range(start,e+1):
            if ansVal<cnt[idx]:
                ansVal = cnt[idx]
                ansIdx = idx
        answer.append(ansIdx)
    return answer

# 접근 2. 성공한 코드 O(e)
 # dp[n] : [n,e] 구간의 최댓값의 idx(=가장 큰 약수의 개수의 idx)
    dp = [0] *(e+1)
    dp[e] = e
    maxVal = cnt[e]
    for i in reversed(range(1,e)):
        # cnt[i]의 값이 [i+1,e]의 최댓값보다 큰 경우(= 더 많이 등장한 경우)
        if cnt[i] >= cnt[dp[i+1]]:
            dp[i] = i
        else:
            dp[i] = dp[i+1]
    
    answer = []
    for start in starts:
        answer.append(dp[start])
    return answer

풀이

아래는 최종 정답 코드이다.

import math
MAX = 5_000_001
def solution(e, starts):
    cnt = [1]*(e+1)
    for num in range(1,e+1):
        for increment in range(num*2,e+1,num):
            cnt[increment]+=1
# -------------------            
    
    # dp[n] : [n,e] 구간의 최댓값의 idx(=가장 큰 약수의 개수의 idx)
    dp = [0] *(e+1)
    dp[e] = e
    maxVal = cnt[e]
    for i in reversed(range(1,e)):
        # cnt[i]의 값이 [i+1,e]의 최댓값보다 큰 경우(= 더 많이 등장한 경우)
        if cnt[i] >= cnt[dp[i+1]]:
            dp[i] = i
        else:
            dp[i] = dp[i+1]
    
    answer = []
    for start in starts:
        answer.append(dp[start])
    return answer

코테에 잘 나오진 않겠지만, 알아두면 좋을 트릭이다. 그리고 dp인줄 몰랐던 dp까지. 상당히 어려운 문제인 것 같다. 프로그래머스 너무 어렵다.