문제
N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.
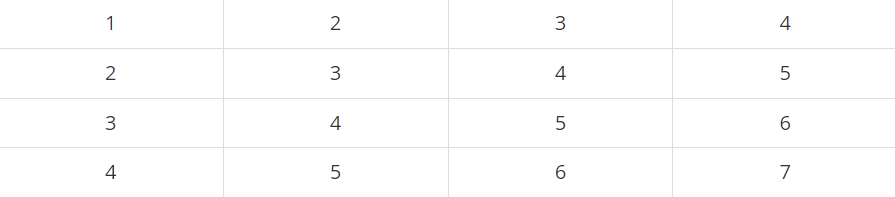
여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
입력
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)
출력
총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.
아이디어
누적합 문제의 2차원 배열버전 문제이다. 먼저 누적합을 나타내는 배열을 구해야 하는데, 이 문제는 2차원 배열의 모든 값을 누적합으로 구하는 문제는 아니다.
예를 들어 (2,2)부터 (3,4)까지의 합을 구할 때는 전체 2차원 배열의 일부분의 합을 구하는 것이다.

따라서 구간 합은 3+4+5+4+5+6=27이 된다. 누적합을 저장할 2차원 배열 (i,j)의 저장될 값을 (1, 1)부터 (i,j)의 누적합을 저장하게 된다.
그리고 문제에서 주어진(x1, y1)~(x2, y2)의 구간 합을 구하기 위해서는 먼저 (1, 1)부터 (x2, y2)의 누적 합에서 포함되지 않은 구간의 합을 제외시켜줘야 한다. 따라서 (1, 1)~(x1-1, y2)의 구간 합과 (1, 1)~(x2, y1-1)의 구간 합을 제외시키고 두 번 제외된 (x1-1, y1-1)에 저장된 값을 더해주면 구간 합을 구할 수 있다.
N, M = map(int, input().split())
nums = [[0]*(N+1)]
answer = []
for i in range(N):
new_num =[0]
for j, num in enumerate(list(map(int, input().split()))):
new_num.append(num + new_num[-1] + nums[i][j+1] - nums[i][j])
nums.append(new_num)
for _ in range(M):
x1, y1, x2, y2 = map(int, input().split())
result = nums[x2][y2] - nums[x1-1][y2] - nums[x2][y1-1] + nums[x1-1][y1-1]
answer.append(result)
for s in answer:
print(s)