• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note9을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Machine Learning

머신 러닝은 지도 학습, 비지도 학습으로 크게 분류할 수 있다.

• 지도 학습(supervised learning): 입력값과 결괏값 사이의 관계를 추론, 새로운 입력값을 통해 결과를 예측하는 알고리즘

• 비지도 학습(unsupervised learning): 특정 결괏값이 없는 입력값을 통해 데이터 간의 구조 등을 알아내는 알고리즘

머신 러닝에 사용하는 데이터셋이 주어지면 대체적으로 세 가지 서브셋으로 나누어 학습에 사용한다.

• 훈련 데이터(training data): 입력값-결괏값을 통해 모델을 학습할 때 사용
• 검증 데이터(validation data): 모델 훈련이 끝난 뒤 성능을 검증할 때 사용. 모델 성능에 따라 하이퍼파라미터를 수정하거나 다른 학습 알고리즘을 적용
• 시험 데이터(test data): 훈련 및 검증에서 사용하지 않은 데이터셋으로 마지막 한 번만 시험용으로 활용

나이브 베이즈

나이브 베이즈 모델은 분류(classification) 문제를 해결할 때 적절한 알고리즘이다.

본 노트에서 나이브 베이즈가 적용되는 전형적인 분류 문제는 스팸 필터링이다.

• 분류 문제: 입력값이 주어지면 각 입력값에 대한 라벨을 통해 분류된다. 훈련 데이터를 통해 입력 데이터와 라벨 간의 관계를 학습, 새로운 데이터가 주어졌을 때 결괏값을 예측한다.

• 특성(feature): 입력 데이터의 어떤 부분을 알고리즘이 학습할 것인지 정해야 한다. 알고리즘은 입력 데이터의 특정 부분을 추출한 뒤 학습한다.

총 $n$개의 특성을 추출해 스팸과 정상 메일 간의 차이를 구별한다고 가정하자.

$P(Y=spam|F_1=f_1,...,F_n=f_n)$
$P(Y=ham|F_1=f_1,...,F_n=f_n)$

모든 메일에서 $n$개의 단어를 특성으로 간주, 추출했다. 각 메일 별로 추출하기 때문에 어떤 단어는 스팸에, 어떤 단어는 정상 메일에, 둘 다 있거나 없는 단어도 있을 것이다. 있다면 $1$, 없다면 $0$으로 표시해 라벨 별로 어떤 단어가 많이 나타나는지 파악할 수 있다는 말이다.

이런 브루트 포스 방법은 기본적인 분류 문제를 해결할 실마리를 던져주지만, 연산량이 매우 크다는 점에서 비현실적이다. 라벨 2개(스팸, 정상)인 위 문제만 하더라도 $n$, 그러니까 추출할 단어의 개수가 $200$개만 되더라도 총 $2^{200+1}$ 개 엔트리에 해당하는 결합 확률 분포표를 계산해야 하기 때문이다.

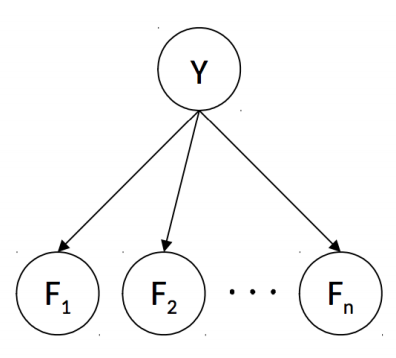
이 브루트 포스 방법에서 잠시 숨을 돌려 나이브 베이즈로 돌아가자. d-separation 규칙을 통해 베이즈 넷의 각 노드 $F_i$가 다른 노드에 대해서 조건적으로 독립인지 구할 수 있다. $Y$가 스팸인지 정상인지 구별하기 위한 엔트리 2개, 이 라벨이 주어질 때 특성 노드 $F_i$ 값을 할당할 엔트리 $4n$개를 합쳐 총 $4n+2$로 시간 복잡도가 대폭 감소했다.

특성 노드 $F$가 주어질 때, 이 특성에 대한 조건부 확률이 가장 큰 라벨 $Y$ 값을 예측하는 식은 다음과 같다.

$prediction(f_1,..,f_n)=argmax_y P(Y=y|F_1=f_1,...,F_N=f_n)=argmax_y P(Y=y, F_1=f_1,...,F_N=f_n)=argmax_y P(Y=y)\prod\limits_{i=i}^{n}P(F_i=f_i|Y=y)$

각 라벨이 주어질 때 특성 노드가 독립적이기 때문에 두 번째 식이 가능하다.

위 문제는 분류 라벨이 두 개인 이진 분류(binary classification) 문제다. 라벨이 두 개 이상인 분류 문제도 존재한다. 이 경우 $k$의 서로 다른 라벨로 입력값을 분류한다고 가정하자.

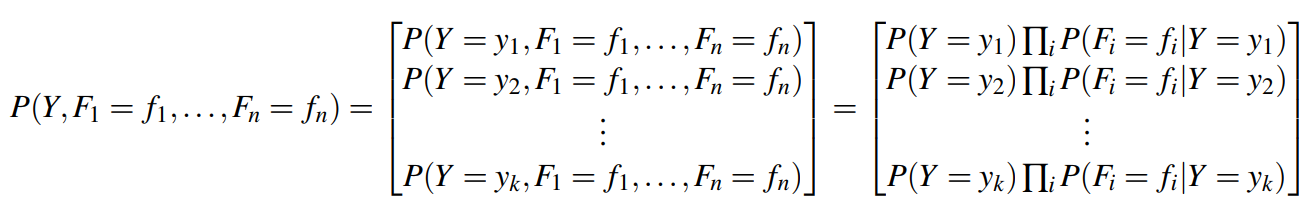
위 식을 한 줄로 간략화하자.
$prediction(F)=argmax_{y_i}P(Y=y_i)\prod\limits_{j}P(F_j=f_j|Y=y_i)$

1. Parameter Estimation

파라미터 추정을 통해 입력 데이터에서 베이즈 넷에서 사용되는 조건부 확률 값을 학습하자. $N$ 개의 샘플 포인트 또는 관측값 집합이 있다고 하자. 미지수 $\theta$가 파라미터 값으로 작용한 확률 분포에서 추출한 $x_1,...,x_N$이 바로 이 관측값 집합이다.

이때 해야 할 일은 주어진 샘플에서 가장 그럴 듯한 파라미터 $\theta$를 학습하는 것이다. 관측값이 동전을 던진 결과(앞면/뒷면)이고 이 확률 분포가 $\theta$라고 가정하자.

주어진 샘플 관측값을 고를 확률을 최댓값으로 만들어주는 파라미터를 찾는 최대 우도 추정, $MLE$ 문제다. $MLE$는 다음과 같은 가정을 따른다.

• 각 샘플값 $x_i$는 같은 확률 분포를 따른다.
• 각 샘플값 $x_i$는 서로 다른 값에 조건부 독립이다.
• 파라미터 $\theta$로 값은 특정 데이터를 얻기 전까지는 균등한 확률(uniform prior)이다.

샘플이 같은 확률 분포를 따르며 서로 조건부 독립이라는 특성을 $i.i.d$ (independent, identically distributed)라고 일컫는다.

우도, $likelihood$는 주어진 확률 분포에서 우리가 얻는 샘플이 추출될 가장 그럴 듯한 경우다.

$L(\theta)=P_{\theta}(x_1,...,x_N)=\prod^N\limits_{i=1}P_{\theta}(x_i)$

위 식을 미분해 최댓값/최솟값이 되는 구간을 얻을 수 있다.

$\frac{\delta}{\delta\theta}L(\theta)=0$

2. Maximum Likelihood for Naive Bayes

스팸 필터링 분류 문제를 $MLE$를 사용해 풀어보자. 필요한 변수들은 다음과 같다.

• $n$(추출할 특성의 개수), $N$(훈련 데이터 개수, 스팸 데이터 $N_s$와 정상 메일 데이터 $N_h$으로 구성), $F_i$(메일 별 추출될 특성 단어, 각 단어가 메일에 존재하면 1, 그렇지 않으면 0), $Y$(스팸 또는 정상 메일로 분류할 라벨), $f_i^{(j)}$($f_i$가 $j$번째 메일에 나타난다면 1, 그렇지 않으면 0)

이진 분류 문제이기 때문에 베르누이 분포를 사용할 수 있다. 양 확률 합이 1이므로 정상 메일 확률을 1에서 뺀 경우를 스팸 메일이라고 간주하자.

우도를 구하는 식은 다음과 같다.

$L(\theta)=\prod^{N_h}\limits_{j=1}P(F_i=f_i^{(j)}|Y=ham)=\prod^{N_h}\limits_{j=1}\theta(f_i^{(j)})(1-\theta)^{1-f_i^{(j)}}$

$j$번째 메일에 $i$번째 특성 $f_i$가 나온다면, 즉 값이 1인 경우 위 식은 $\theta^1(1-\theta)^0=\theta$, 값이 0인 경우라면 $\theta^0(1-\theta)^1=(1-\theta)$다.

우도 $L$을 미분해 최댓값을 구하자. 로그를 통해 풀면 수월하다.

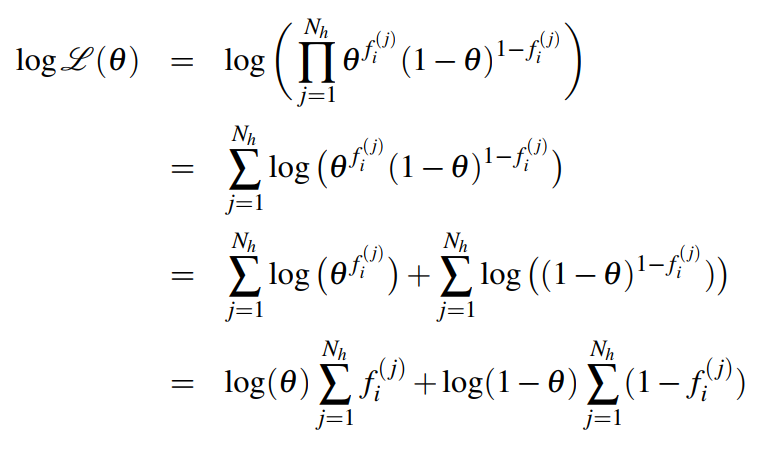
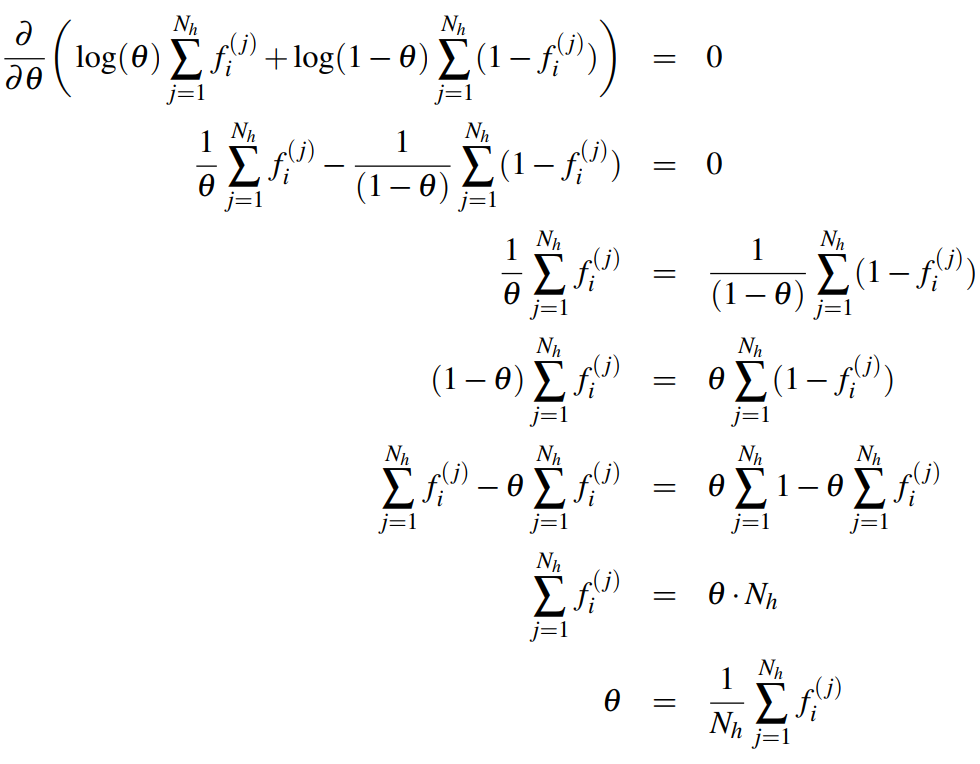
정상 메일 확률 $MLE$는 특성 $i$번째가 나타나는 정상 메일의 개수를 모든 정상 메일 개수로 나눈 값이다. 직관적인 생각과도 일치한다.

3. Smoothing

훈련 데이터셋으로 모델을 학습한 정도가 과도해진다면 훈련 데이터셋이 아닌 다른 데이터셋에는 적절한 예측값을 내놓지 못할 수 있다. 이를 과적합(overfitting)이라고 부르며 일반적인 데이터셋에 사용되기 위해 지양해야 한다.

나이브 베이즈 분류 모델의 과적합을 라플라스 스무딩(Laplace smoothing)을 통해 낮출 수 있다. 결괏값을 $x$라고 할 때 그 개수를 $count(x)$라고 표현할 수 있을 것인데, 이때 추가 $k$개를 더 준다고 가정한다.

$P_{MLE}(x)=\frac{count(x)}{N}$
$P_{LAP,k}(x)=\frac{count(x)+k}{N+k|X|}$

$k$개를 여분으로 더 봤다는 말은 곧 전체 $X$ 클래스의 인스턴스를 $k$개 더 봐야 한다는 말이므로 $k|X|$를 분모에 더해야 한다.

조건부 확률을 구할 때에도 라플라스 스무딩이 적용되기 때문에 $P_{LAP,k}(x|y)=\frac{count(x,y)+k}{count(y)+k|X|}$이다. $k$가 0인 경우, 무한히 많아지는 경우는 다음과 같다.

• $P_{LAP,0}(x)=P){MLE}(x)$
• $P_{LAP,\infty}(x)=\frac{1}{|X|}$

$k$가 하이퍼 파라미터이기 때문에 과적합 정도를 조정하는 건 모델 설계자의 몫이다. 검증 데이터셋에 학습 모델을 적용해 과적합 정도를 파악하자.