
Basic Concepts
시스템 생애 주기
- 입력값 / 출력값
- Bottom-up / Top-down
- 데이터 객체: ADT(abstract data types)
- 연산: 알고리즘
포인터
- C 언어: 메모리 주소를 표현하는 방법. 객체가 담긴 주소 참조
&: 주소 연산자*: 참조 연산자
동적 할당
- 데이터 입력값에 따라 배열 크기가 달라지는 경우 → 동적으로 사이즈 결정 필요
- C 언어: malloc으로 메모리 할당 / free로 메모리 해제
알고리즘의 정의
- 특정 작업을 수행하는 일련의 유한한 명령어 집합
선택 정렬
public func selectionSort<Element>(_ array: inout [Element]) where Element: Comparable {
guard array.count >= 2 else { return }
// 비교 X
for cur in 0..<array.count-1 {
// cur 번째 가장 작은 수 구하기
var lowest = cur
for other in (cur+1)..<array.count {
if array[lowest] > array[other] {
lowest = other
}
}
// 현 시점 배열 내에서 가장 "작은" 값이 담긴 인덱스 lowest
if lowest != cur {
array.swapAt(lowest, cur)
}
}
}이진 탐색
- 반복
public func binarySearchIterative<Element>(_ array: [Element], _ searchedItem: Element) -> Int where Element: Comparable {
var left = 0
var right = array.count-1
while left < right {
let middle = (left + right) / 2
if searchedItem == array[middle] {
return middle
} else if searchedItem > array[middle] {
left = middle + 1
} else {
right = middle - 1
}
}
return -1
}
var array = [1, 2, 3, 4, 5, 100, -1, 20, 30]
let wrongIdx = binarySearchIterative(array, 30)
// -1 -> 정렬되지 않은 배열을 파라미터로 전달
array.sort()
// [-1, 1, 2, 3, 4, 5, 20, 30, 100] -> 정렬된 배열을 파라미터로 전달
let rightIdx = binarySearchIterative(array, 30)
print(rightIdx)
// 7- 재귀
public func binarySeachRecursive<Element>(_ array: [Element], _ searchItem: Element, _ left: Int, _ right: Int) where Element: Comparable {
if left <= right {
let middle = (left + right) / 2
if searchItem == array[middle] {
idx = middle
} else if searchItem > array[middle] {
binarySeachRecursive(array, searchItem, middle + 1, right)
} else {
binarySeachRecursive(array, searchItem, left, middle - 1)
}
}
}
var idx = -1
var array = [30, 2, 3, 4, 5, 100, -1, 20, 1]
binarySeachRecursive(array, 30, 0, array.count-1)
// -1 -> 정렬되지 않은 배열을 파라미터로 전달
array.sort()
// [-1, 1, 2, 3, 4, 5, 20, 30, 100] -> 정렬된 배열을 파라미터로 전달
binarySeachRecursive(array, 30, 0, array.count-1)
// 7순열
- 재귀
public func permutatinRecursive<Element>(_ array: [Element]) {
if targetArray.count == array.count {
print(array)
guard let array = array as? [Int] else { return }
resultArray.append(array)
return
}
for idx in 0..<targetArray.count {
if !checked[idx] {
checked[idx] = true
permutatinRecursive(array + [targetArray[idx]])
checked[idx] = false
}
}
}
var targetArray = [1, 2, 3]
var checked = Array(repeating: false, count: targetArray.count)
var resultArray = [[Int]]()
permutatinRecursive([])
// [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]데이터 추상화
- 객체의 집합 + 객채에서 이루어지는 연산의 집합
- 사용자로부터 데이터 타입의 객체 표현을 숨기는 것이 좋은 디자인 방법 → 제공한 함수만으로 원하는 기능을 발휘하도록 만들기
ADT
- Abstract Data Type: 객체를 구체적으로 표현한 내용과 그 객체에 대한 연산이 객체 표현 및 연산 구현과 분리되어 있는 방식
데이터 타입을 추상적으로 만들어야 한다. 파이썬, 자바 등 특정 언어로부터 독립적으로 기능하도록(
implementation-independent)! - Creator: 새로운 인스턴스를 생성하는 함수
- Transformer: 다른 인스턴스를 통해 특정 인스턴스를 생성하는 함수
- Observer: 인스턴스 정보를 보여주는 함수
자연수의 ADT

퍼포먼스 분석
- 프로그램이 주어진 작업의 구체적인 양식을 충족하는지?
- 정확히 작동하는지?
- 사용법 및 작동 양식을 보여주는 문서가 있는지?
- 프로그램이 논리적 양식에 따라 작동하는지?
- 가독성 있는 코드인지?
- 프라이머리/세컨더리 스토리지를 효율적으로 쓰는지?
- 러닝 타임이 적절한지?
공간 복잡도
- 실행이 마무리될 때까지 걸리는 메모리 사용량
- : 입력/출력 값 및 사이즈에 독립적인 변수.
- : 특정 인스턴스 값에 의존적인 변수
일반적으로 공간 복잡도는 에 따라서 결정된다!
- 일반적으로 메모리 사용량보다 연산 속도가 더 중시된다.
시간 복잡도
- 실행이 마무리될 때까지 걸리는 컴퓨터 시간
- 컴파일 시간 와 실행 시간 의 합
특정 알고리즘의 퍼포먼스를 측정하는 건 쉽지 않기 때문에 간략화된 방식이 필요하다!
Big-Oh 표기법
빅-오 표현 방법은
upper bound임에 주의하자!- : constant
- : linear
- : quadratic
- : exponential
- : logarithmic
- : log linear
이 밖에도
lower bound인 빅-오메가,lower and upper bound인 빅-세타 표기 방법이 존재하지만, 빅-오가 가장 전반적으로 두루 사용되는 시간 복잡도 표기 방법이다!
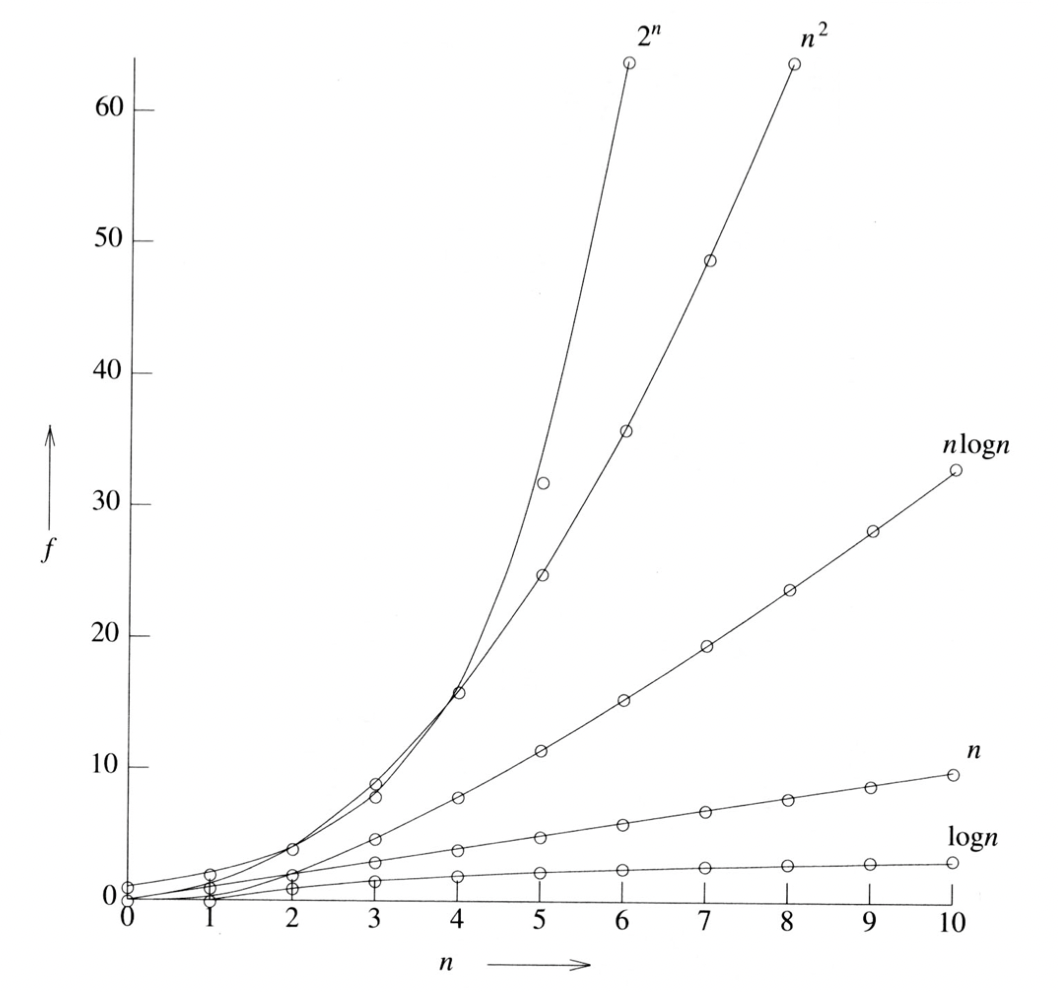
n이 선형적으로 증가하지만 연산 필요 시간은 알고리즘의 효율성에 따라서 엄청난 격차가 벌어지기 때문에, 효율적인 알고리즘을 짜는 게 연산 시간을 줄이는 데 필수적이다!
