기초 수학

본격적으로 파이썬 코드에 잘 활용되는 기초 수학 개념들에 대해 학습하고 정리해보기로 한다.

1. 약수 / 소수

바로 문제 풀이를 통해 어떻게 코드적으로 구현하는지 살펴본다.

Ex 1.약수

# 사용자가 입력한 숫자의 약수를 출력
inputNum = int(input('0보다 큰 정수 입력: '))

for i in range(1, (inputNum + 1)):
    if inputNum % i == 0: # 나눠떨어지면 약수
        print(f'{inputNum}의 약수: {i}')

Ex 2. 소수

# 사용자가 입력한 숫자까지의 소수 찾기
inputNum = int(input('0보다 큰 정수 입력: '))

for num in range(2,(inputNum + 1)):
    flag = True
    for n in range(2,num):
        if num % n == 0:
            flag = False
            break

    if flag:
        print(f'{num}: 소수!')
    else:
        print(f'{num}: 합성수!')

2. 소인수분해

말 그대로, 소인수 : 소수 + 약수라서

약수 중에서 소수인 숫자를 소인수라고 보면 된다.

따라서 소인수 분해는

어떤 수를 소인수로 분해하는 것을 말한다.

✅ 소인수분해를 이용해서 약수를 구할 수도 있다. ✅

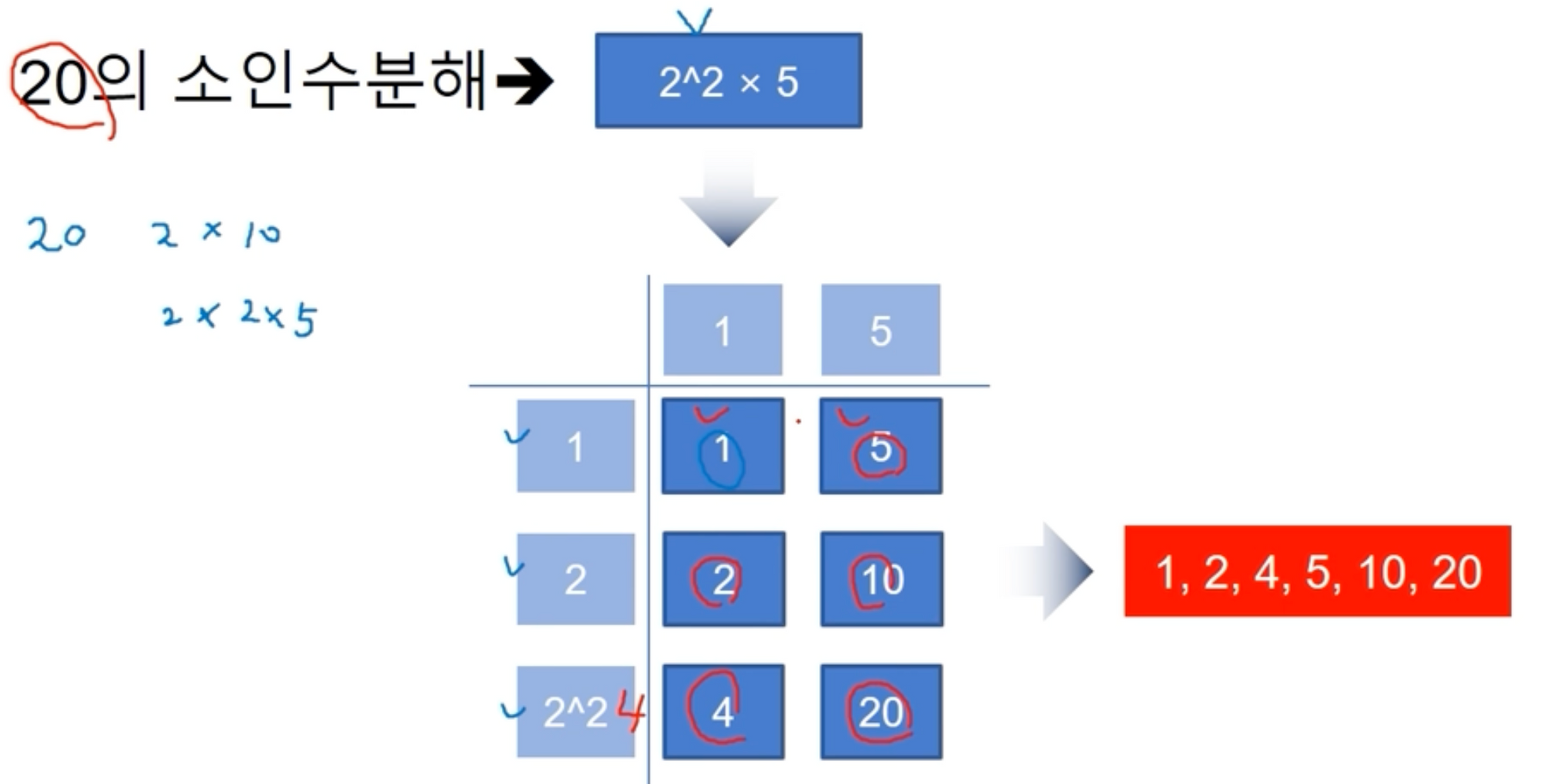
🔻연습 문제🔻

# 입력한 수를 소인수분해하자.
inputNum = int(input('1보다 큰 정수 입력: '))

n = 2
while n <= inputNum:
    if inputNum % n == 0:
        print(f'소인수 : {n}')
        inputNum /= n
    else:
        n += 1

# 72에 x를 곱하면 y의 제곱이 된다고 할 때, x에 해당하는 가장 작은 정수를 구하자.

inputNum = int(input('1보다 큰 정수 입력: '))

n = 2
numlist = []
while n <= inputNum:
    if inputNum % n == 0:
        print(f'소인수 : {n}')
        if numlist.count(n) == 0: # numlist 에 없고, 처음 나왔다면
            numlist.append(n)
        elif numlist.count(n) == 1: # 이미 들어있기 때문에, 그냥 신경쓸 필요 없다. -> 제거하자
            numlist.remove(n)

        inputNum /= n
    else:
        n += 1

print(f'searchNumber : {numlist}')

3. 최대공약수

소인수분해를 이용하면 최대공약수 및 공약수를 구할 수 있다.

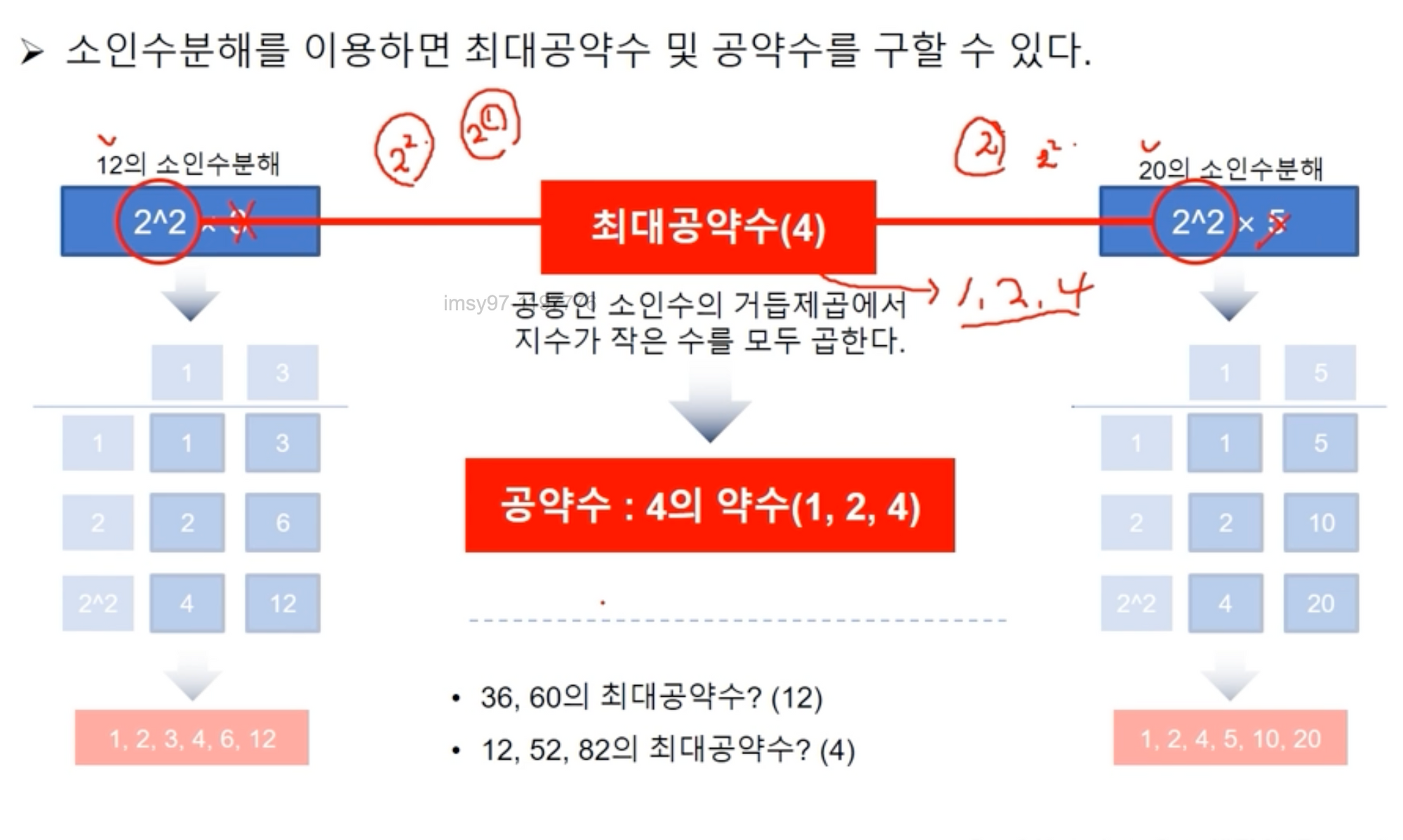
🔻연습 문제🔻

# 두 개의 수를 입력하면 공약수와 최대공약수를 출력하는 코드를 작성하자.
n1 = int(input('1보다 큰 정수 입력: '))
n2 = int(input('1보다 큰 정수 입력: '))

max_num = 0
for i in range(1, (n1 + 1)):
    if n1 % i == 0 and n2 % i == 0:
        print(f'공약수 : {i}')
        max_num = i

print(f'최대공약수 : {max_num}')

# 세 개의 수를 입력하면 공약수와 최대공약수를 출력하는 코드
n1 = int(input('1보다 큰 정수 입력: '))
n2 = int(input('1보다 큰 정수 입력: '))
n3 = int(input('1보다 큰 정수 입력: '))

maxNum = 0
for i in range(1,(n1 + 1)):
    if n1 % i == 0 and n2 % i == 0 and n3 % i == 0: # 세 값에 모두 나눠떨어지면 공약수
        print(f'공약수 : {i}')
        maxNum = i
print(f'최대공약수 : {maxNum}')

유클리드 호제법

유클리드 호제법을 이용해서 최대공약수를 구할 수 있다.

• x, y의 최대공약수는 y와 (x%y) 의 최대공약수와 같다.

🔻연습 문제🔻

n1 = int(input('1보다 큰 정수 입력: '))
n2 = int(input('1보다 큰 정수 입력: '))

temp1 = n1
temp2 = n2

while temp2 > 0:
    temp = temp2
    temp2 = temp1 % temp2
    temp1 = temp

print(f'{n1},{n2}의 최대공약수:  {temp1}')

# 최대공약수를 가지고 공약수를 구하기
for n in range(1,(temp1 + 1)):
    if temp1 % n == 0:
        print(f'{n1}, {n2}의 공약수 : {n}')

3. 최소공배수

최대공약수를 이용해서 최소공배수 구할 수 있다.

# 두 개의 수를 입력하면 최소공배수를 출력하는 코드를 작성하자.
n1 = int(input('1보다 큰 정수 입력: '))
n2 = int(input('1보다 큰 정수 입력: '))
maxNum = 0

for i in range(1, (n1 + 1)):
    if n1 % i == 0 and n2 % i == 0:
        print(f'공약수 : {i}')
        maxNum = i

print(f'최대공약수: {maxNum}')

minNum = (n1 * n2) // maxNum # 최소공배수
print(f'최소공배수: {minNum}')

# 세 개의 수를 입력하면 최소공배수를 출력하는 코드를 작성하자.
n1 = int(input('1보다 큰 정수 입력: '))
n2 = int(input('1보다 큰 정수 입력: '))
n3 = int(input('1보다 큰 정수 입력: '))
maxNum = 0

for i in range(1, (n1 + 1)):
    if n1 % i == 0 and n2 % i == 0:
        maxNum = i

print(f'최대공약수: {maxNum}')

minNum = (n1 * n2) // maxNum # 최소공배수
print(f'{n1}, {n2}의 최소공배수: {minNum}')

newNum = minNum
for i in range(1, (newNum + 1)):
    if newNum % i == 0 and n3 % i == 0:
        maxNum = i

print(f'최대공약수: {maxNum}')

minNum = (newNum * n3) // maxNum # 최소공배수
print(f'{n1}, {n2}, {n3}의 최소공배수: {minNum}')

4. 진법

• 2진수 → 8진수 변환

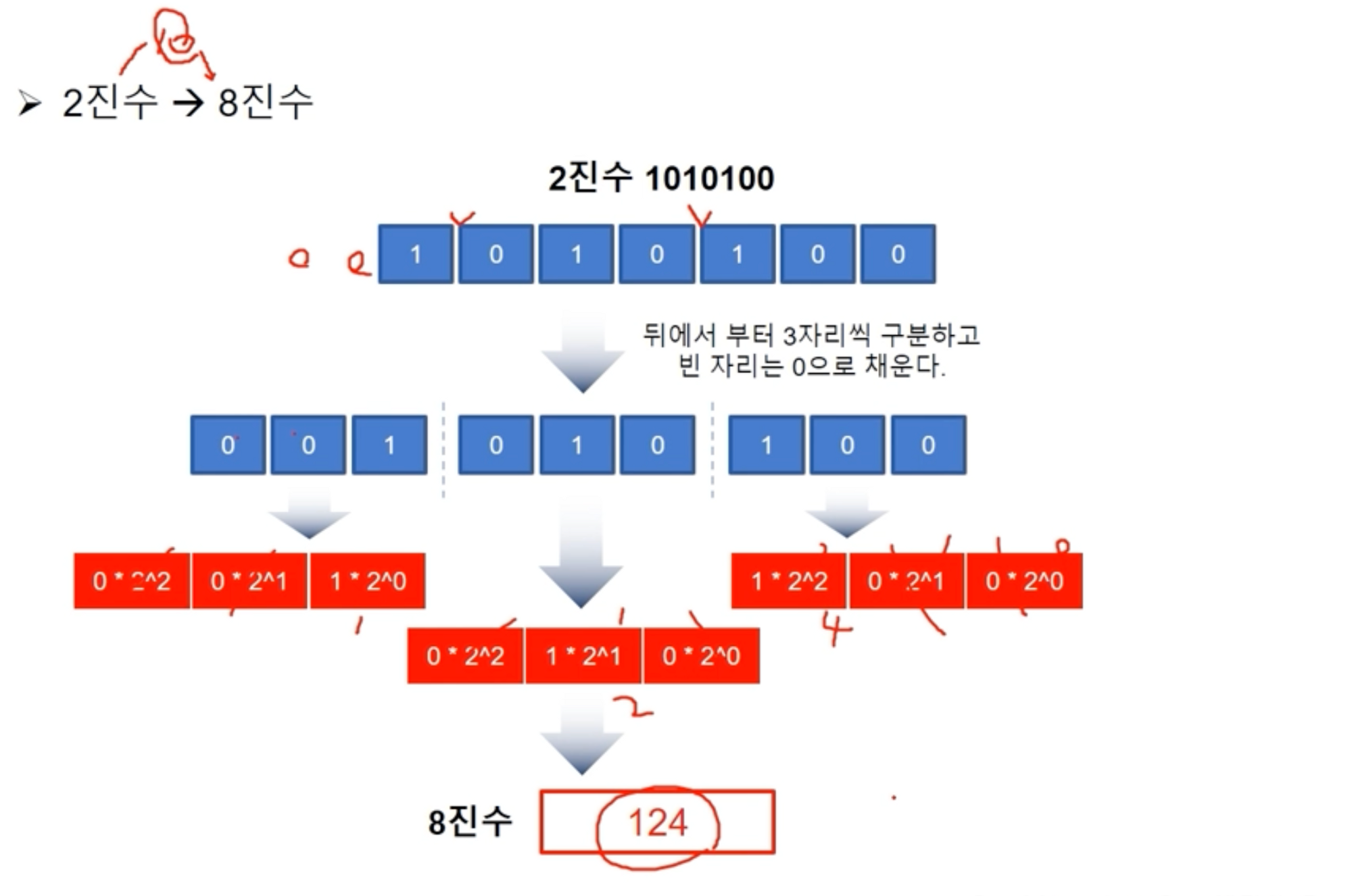
• 2진수 → 16진수

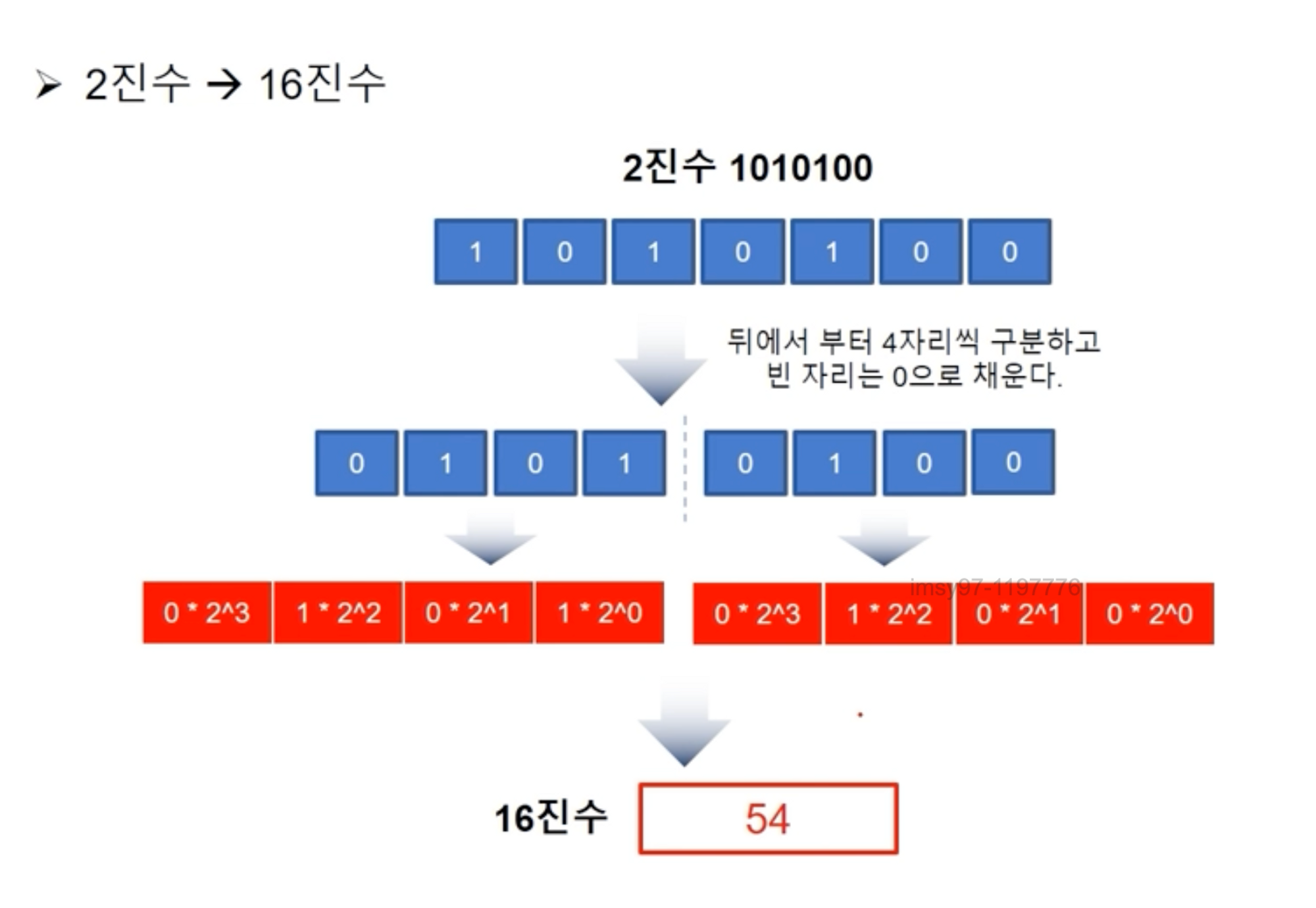
파이썬에서의 진법 변환

10진수 → 2진수, 8진수, 16진수
- bin() : 2진수로 변환
- oct() : 8진수로 변환
- hex() : 16진수로 변환

• 이외에도 format() 함수로도 바꿀 수 있다.

  dNum = 30
  print('2진수: {}'.format(format(dNum, '#b'))) # 또는 '0b'를 빼고 출력하고 싶다면 'b' 만 써준다.
  print('8진수: {}'.format(format(dNum, '#o'))) # 또는 'o'
  print('16진수: {}'.format(format(dNum, '#x'))) # 또는 'x'
  
  # 또는 아래와 같이 사용할 수도 있다.
  print('{0:#b} , {0:#o},  {0:#x}'.format(dNum))

X진수 → 10진수
- int() 를 사용한다.

X진수 → X진수
- 8진수로 변환 : oct()
- 2진수로 변환 : bin()
- 16진수로 변환 : hex()
- 10진수로 변환 : int()

---

🔜 다음 스터디 노트..

다음 스터디 노트에서는 수열 과 관련된 개념들과, 팩토리얼, 순열, 조합, 확률 에 대한 개념들을 학습하고, 정리해보도록 한다.