문제 설명
하드디스크는 한 번에 하나의 작업만 수행할 수 있습니다. 디스크 컨트롤러를 구현하는 방법은 여러 가지가 있습니다. 가장 일반적인 방법은 요청이 들어온 순서대로 처리하는 것입니다.
- 0ms 시점에 3ms가 소요되는 A작업 요청
- 1ms 시점에 9ms가 소요되는 B작업 요청
- 2ms 시점에 6ms가 소요되는 C작업 요청
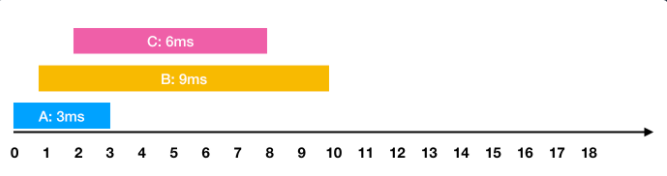
한 번에 하나의 요청만을 수행할 수 있기 때문에 각각의 작업을 요청받은 순서대로 처리하면 다음과 같이 처리 됩니다.

이 때 각 작업의 요청부터 종료까지 걸린 시간의 평균은 10ms(= (3 + 11 + 16) / 3)가 됩니다.
하지만 A → C → B 순서대로 처리하면

이렇게 A → C → B의 순서로 처리하면 각 작업의 요청부터 종료까지 걸린 시간의 평균은 9ms(= (3 + 7 + 17) / 3)가 됩니다.
제한 사항
jobs의 길이는 1 이상 500 이하입니다.
jobs의 각 행은 하나의 작업에 대한 [작업이 요청되는 시점, 작업의 소요시간] 입니다.
각 작업에 대해 작업이 요청되는 시간은 0 이상 1,000 이하입니다.
각 작업에 대해 작업의 소요시간은 1 이상 1,000 이하입니다.
하드디스크가 작업을 수행하고 있지 않을 때에는 먼저 요청이 들어온 작업부터 처리합니다.
풀이
처음 이 문제를 봤을 때, 스케줄링 문제에서 대기시간을 포함하기만 하면 될것 같았다. 문제 분류로 힙이 적혀있었지만 힙 구조를 사용하지 않고 한번 해 봤다.
힙 X
- 끝나는 시간을 기준으로 정렬
- 시작시간에 요청이 있으면 작업이 끝나는 지점으로 시작시간 옮겨줌.
- 요청에서 처리까지 걸리는 시간을 answer에 더해줌.
- 작업이 끝났기에 리스트에서 pop 시켜줌.
- 리스트가 모두 pop 될때까지 반복.
def solution(jobs):
answer = 0
jobs_num = len(jobs)
jobs = sorted(jobs, key = lambda x : x[1])
start = 0
while len(jobs) != 0 :
for i in range (0,len(jobs)):
if jobs[i][0] <= start :
start += jobs[i][1]
answer += abs(jobs[i][0] - start)
jobs.pop(i)
break;
if i == len(jobs) -1 :
start +=1
return answer // jobs_num놀랍게도 정답이었다...그러나 힙의 카테고리에 들어있으니...힙을 사용한 풀이도 공부해 보았다.
힙
힙을 사용한다는 것은 우선순위 큐를 사용한다는 말로 유추할 수 있다. 그렇다면 우선순위 큐를 사용하는 이유는 무엇인가?
바로 파이썬 내장함수인 sort() 보다 빠르기 때문이다.
sort()도 사실 제법 빠른 편이지만, 이 sort() 를 이기는게 우선순위 큐. 즉, heapq이다. 그래서 위의 풀이와 다른 점이라고는 sort()로 한꺼번에 정렬을 시킨 것과 다르게 heapq를 사용해 정렬을 해 나가며 가장 작업시간이 작은순으로 정렬을 하는 것이다. 정리하자면,
- 현재 시간 계산( 처음엔 0 )
- 현재 시간보다 요청 시간이 작은 작업을 힙큐에 넣어줌.
heappop()으로 가장 짧은 작업의 끝나는 시간을 현재 시간으로 설정.- 해당 작업의 대기시간 + 작업시간을 따로 저장.
- 리스트가 모두 pop 될때까지 반복.
import heapq
def solution(jobs):
answer , now , end = 0,0, -1
wait , n , cnt = [], len(jobs), 0
while cnt < n :
for j in jobs :
if end < j[0] <= now :
answer += now - j[0]
heapq.heappush(wait,j[1])
if not wait:
now += 1
continue
t = heapq.heappop(wait)
answer += len(wait) * t
end = now
now += t
cnt += 1
return answer//n