배열
배열은 값 또는 변수 엘리먼트의 집합으로 구성된 구조로, 하나 이상의 인덱스 또는 키로 식별된다.

-
자료구조는 크게 메모리 공간 기반의 연속 방식과 포인터 기반의 연결 방식으로 나뉜다. 배열은 이 중에서 연속 방식의 가장 기본이 되는 자료형이다.
-
배열은 크기를 지정하고 해당 크기만큼의 연속된 메모리 공간을 할당받는 작업을 수행하는 자료형을 말하는데, 크기가 고정되어 있으며 한번 생성한 배열은 크기를 변경하는 것이 불가능하다.
-
배열은 어느 위치에나 O(1)에 조회가 가능하다는 장점이 있다. 즉시 주소를 계산할 수 있고, 언제든 해당 메모리 주소에 있는 값을 O(1)에 조회가 가능하다.
연결 리스트
연결 리스트는 데이터 요소의 선형 집합으로, 데이터의 순서가 메모리에 물리적인 순서대로 저장되지는 않는다.
-
연결 리스트는 컴퓨터과학에서 배열과 함께 가장 기본이 되는 대표적인 선형 자료구조 중 하나로 다양한 추상 자료형 구현의 기반이 된다.
-
동적으로 새로운 노드를 삽입하거나 삭제하기가 간편하며, 연결 구조를 통해 물리 메모리를 연속적으로 사용하지 않아도 되기 때문에 관리도 쉽다. 또, 데이터를 구조체로 묶어서 포인터로 연결한다는 개념은 여러가지 방법으로 다양하게 활용이 가능하다.
-
연결 리스트는 배열과는 달리 특정 인덱스에 접근하기 위해서는 전체를 순서대로 읽어야 하므로 상수 시간에 접근할 수 없다.
-
탑색에는 O(n)이 소요되며, 시작 또는 끝 지점에 아이템을 추가하거나 삭제, 추출하는 작업은 O(1)에 가능하다.
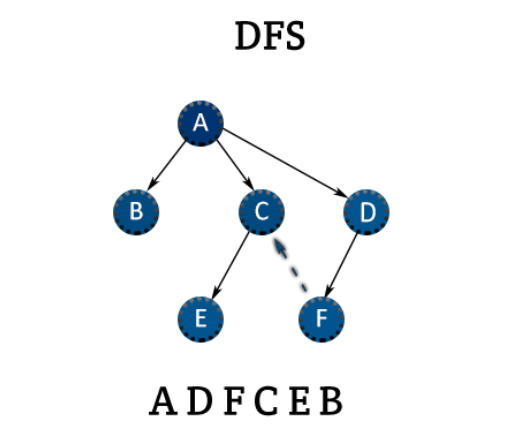
DFS (깊이 우선 탐색)
-
DFS는 19세기 프랑스의 수학자 찰스 피에르 트레모가 미로 찾기를 풀기 위한 전략을 찾다 고안한 것으로 알려져 있으며, 일반적으로 BFS에 비해 더 널리 쓰인다.
-
주로 스택으로 구현하거나 재귀로 구현하며, 백트래킹을 통해 뛰어난 효용을 보인다.
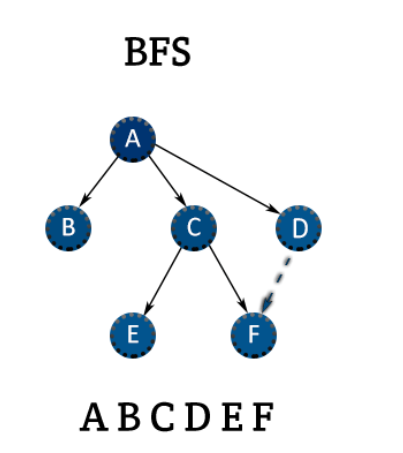
BFS (너비 우선 탐색)
-
BFS는 주로 큐로 구현하며, 그래프의 최단 경로를 구하는 문제 등에 사용된다.
-
BFS는 DFS보다 쓰임새는 적지만, 최단 경로를 찾는 다익스트라 알고리즘 등에 매우 유용하게 쓰인다.