알고리즘에 대해 알아보자!
- 근삿값
- 평균
- 재귀
- 하노이의 탑
- 병합 정렬
- 퀵 정렬

10. 근삿값
특정 값(참값)에 가장 가까운 값을 근삿값이라고 한다.
import random
nums = random.sample(range(0, 50), 20) # 중복되면 안되서 .sample()로 구성
print(f'nums : {nums}')
# ▼ 근삿값 알고리즘
inputNum = int(input('input number : '))
print(f'inputNum : {inputNum}')
nearNum =0 #우리가 찾고 싶은 값
minNum =50 #가장 큰 값으로 설정, 50만큼 차이가 난다..?
for n in nums:
#▼ 차이를 구해야 함
absNum = abs(n - inputNum) # 음수가 나올 수 있으므로 절대값을 씌워 줌 #abs : 절대값
if absNum < minNum: # 작으면
minNum = absNum # 재설정
nearNum = n # 사용자가 입력한 숫자에서 가장 가까운 값은 n 이라고 설정
print(f'nearNum: {nearNum}')▼
nums : [13, 48, 36, 23, 20, 10, 29, 47, 22, 27, 30, 28, 33, 44, 41, 5, 43, 25, 15, 32]
input number : 17
inputNum : 17
nearNum: 15🏷️실습
근삿값 알고리즘을 이용해서 시험 점수를 입력하면 학점이 출력되는 프로그램을 만들어보자. 평균 점수에 따른 학점 기준 점수는 다음과 같다

- near.py
#학점 구하기
def getNearNum(an):
baseScores = [95,85,75,65,55] #1. 95에 근삿값이면 A학점...부분
nearNum = 0
minNum = 100 #2. minNum : 점수, 가장 큰 점수로 일단 초기값 설정
#▼근사값을 찾는 for()문
for n in baseScores: #3. bascores 만큼 돌아가서
#4. 차이를 구해야 함
absNum = abs(n - an) #5. n에서 사용자가 입력한 값(an)을 뺴줌, 절대값(abs) 처리
if absNum < minNum:
minNum = absNum
nearNum = n #6. 점수를 찾음
#7. ▼ 근사값에 따른 점수를 출력하는 문장
if nearNum == 95:
return 'A'
elif nearNum == 85:
return 'B'
elif nearNum == 75:
return 'C'
elif nearNum == 65:
return 'D'
elif nearNum <= 55:
return 'F'- nearEx.py : 실행파일
import near
scores = []
kor = int(input('국어 입력 : '))
scores.append(kor)
eng = int(input('영어 입력 : '))
scores.append(eng)
mat = int(input('수학 입력 : '))
scores.append(mat)
sci = int(input('과학 입력 : '))
scores.append(sci)
his = int(input('국사 입력 : '))
scores.append(his)
totalScore = sum(scores)
print(f'총점 : {totalScore}')
avgScore = totalScore / len(scores)
print(f'평균 : {avgScore}')
#8. 근사값 구하기
grade = near.getNearNum(avgScore) #9. 학점이 반환 됨
print(f'학점 : {grade}')▼
국어 입력 : 45
영어 입력 : 71
수학 입력 : 82
과학 입력 : 69
국사 입력 : 90
총점 : 357
평균 : 71.4
학점 : C11. 평균
여러 수나 양의 중간값을 갖는 수를 평균이라고 한다
- 기본 모양 (1)
import random
nums = random.sample(range(0,100), 10)
print(f'nums : {nums}')
total =0
for n in nums: # 10개의 수를 발생 시킴
total += n # 발생할때 마다, 총 10개의 수를 다 더함 = 총합계
average = total / len(nums) # 평균을 구함 : 총합 / 총 길이(개수)
print(f'average: {round(average, 2)}') # 출력- 기본 모양(2)
# 50 이상, 90이하 수들의 평균
nums = random.sample(range(0,100), 30)
print(f'nums : {nums}')
total =0
targetNums = []
for n in nums:
if n >= 50 and n <= 90:
total += n
targetNums.append(n)
average = total / len(targetNums)
print(f'targetNums: {targetNums}')
print(f'average: {round(average, 2)}')- 기본모양 (3) 정수들 만의 평균 구하기
nums = [4,5,12,0,5,7.34,9.1,9,3,3.159,1,11,12.789]
print(f'{nums}')
targetNums = []
total =0
for n in nums:
if n - int(n) == 0: # = 이건 정수란 얘기
total += n
targetNums.append(n)
average = total / len(targetNums)
print(f'average: {round(average, 2)}')
print(f'targetNums :{targetNums}')🏷️실습
★ 풀이 방법 : 평균 + 순위 알고리즘
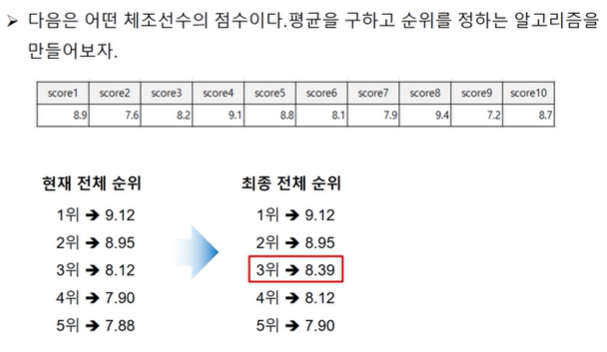
- 근사값 알고리즘 : near.py
#근삿값 알고리즘 활용
class Top5Players:
#1. 값 설정 & 초기화
def __init__(self, cs, ns):
self.currentScore = cs
self.newScore = ns
#2. 어디에 끼어들어갈지 재정의
def setAlignScore(self):
nearIdx =0 #근사값 인덱스
nearScore =0 # 근사값
minNum =10.0 # 최소
#3. 가장 가까이에 있는 인덱스, 점수 구하기
for i, s in enumerate(self.currentScore):
absNum = abs(self.newScore - s)
if absNum < minNum:
minNum = absNum
nearIdx = i
nearScore = s
#4. 찾아 들어갈 자리 선정
if self.newScore >= self.currentScore[nearIdx]: #5. 가장 가까운 숫자(nearIdx)보다 크거나 같다면
#6. 하나씩 뒤로 밀려나야 함
for i in range(len(self.currentScore)-1, nearIdx, -1): #7. (self.currentScore)-1 ~ nearIdx 까지, -1 씩
self.currentScore[i] = self.currentScore[i-1] #8. 하나 밀려남
self.currentScore[nearIdx] = self.newScore #9. 새로운 점수를 밀려난 자리에 넣어 줌
#10. 작은 경우
else:
for i in range(len(self.currentScore)-1, nearIdx +1, -1):
self.currentScore[i] = self.currentScore[i-1]
self.currentScore[nearIdx] = self.newScore
def getFinalTop5Scores(self):
return self.currentScore- 실행문 : avg.py
#11. class 불러옴
import near
scores = [8.9,7.6,8.2,9.1,8.8,8.1,7.9,9.4,7.2,8.5]
top5PlayerScores = [9.12,8.95,8.12,7.90,7.88]
print(f'top5PlayerScores :{top5PlayerScores}')
total =0
average =0
for n in scores:
total += n
average = round(total / len(scores), 2)
print(f'total : {total}')
print(f'average : {average}')
#12. near 모듈에서 Top5Players 모듈을 만듬
tp = near.Top5Players(top5PlayerScores, average)
#13. 레퍼런스 호출해 정렬을 다시 함
tp.setAlignScore()
top5PlayerScores = tp.getFinalTop5Scores()
print(f'top5PlayerScores : {top5PlayerScores}')▼
top5PlayerScores :[9.12, 8.95, 8.12, 7.9, 7.88]
total : 83.7
average : 8.37
top5PlayerScores : [9.12, 8.95, 8.37, 8.12, 7.9]12. 재귀(factorial_!)
재귀알고리즘 이란?
나 자신을 다시 호출하는 것
10 -> (num)으로 호출 -> recusion(num-1)로 호출 -> (num)으로 호출 -> ....
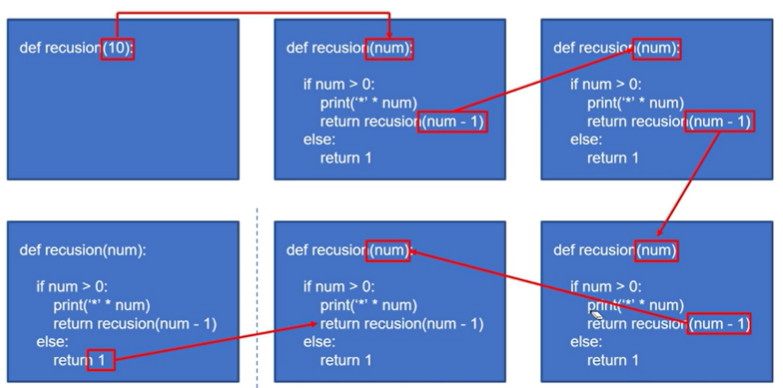
- 방법 (1) : recusion + if()
def recusion(num):
#1. 재귀함수는 if()조건문을 포함 함, 그렇지 않은 경우 무한루프에 빠짐
if num > 0: #2. 0보다 큰 경우에만 '나'를 호출하겠다
print('*' * num) # 3. num 갯수 만큼 *을 찍겠다
return recusion(num-1) # 4.'나'를 반환해줌, 1자리 뺴서 (=10-9-8->7 순으로 반복되야 하기 때문)
else:
return 1 #5. num이 0이 되는 순간, 1을 반환해 주겠다
recusion(10) # 나는 10개의 *로 시작하겠다.- 방법(2) : factorial !이용
def factorial(num):
if num > 0:
return num * factorial(num-1) #재호출 = (n-1)_
else:
return 1
print(f'factorial(10) {factorial(10)}')▼
factorial(10) 3628800🏷️실습
- 방법(1) : 반복문 이용
def greatestCommoDevide(n1, n2):
maxNum = 0 #1. 최대공약수 선언
for i in range(1, (n1 +1)):
if n1 % i == 0 and n2 % i == 0: #2.공약수가 구해짐
maxNum = i #3. i를 maxNum에 할당해 줌
return maxNum
print(f'greatestCommoDevide(82, 32) :{greatestCommoDevide(82, 32)}')
print(f'greatestCommoDevide(96, 40) :{greatestCommoDevide(96, 40)}')▼
greatestCommoDevide(82, 32) :2
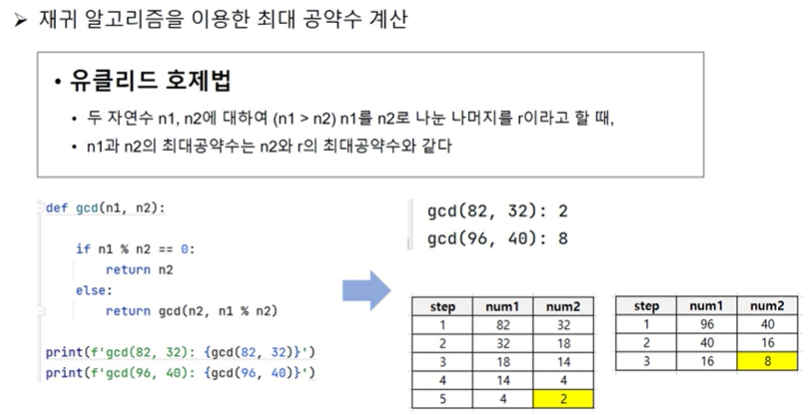
greatestCommoDevide(96, 40) :8- 방법(2) : 재귀함수 이용
def gcd(n1, n2):
if n1 % n2 == 0:
return n2
else:
return gcd(n2, n1 % n2) # 재귀함수를 이용해 , 다시 '나' 자신을 호출
print(f'gcd(82,32) : {gcd(82,32)}')
print(f'gcd(96,40) : {gcd(96,40)}')▼
gcd(82,32) : 2
gcd(96,40) : 813. 하노이의 탑
하노이의 탑 이란?
퍼즐게임의 일종으로 3개의 기둥을 이용해 원판을 다른 기둥으로 옮기면 되고, 제약 조건은 다음과 같다.
1. 한번에 1개의 원판만 옮길 수 있다
2. 큰 원판이 작은 원판 위에 있어서는 안된다
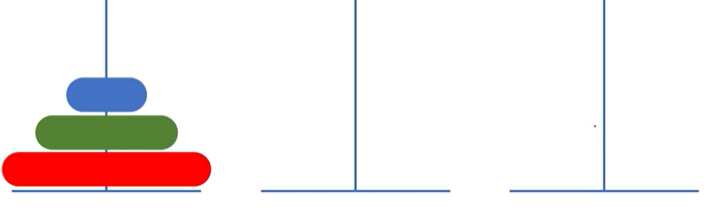
🏷️실습
#1. def moveDisc(원판 개수, 출발 기둥, 도착 기둥, 경유 기둥)
def moveDisc(discCnt, fromBar, toBar, viaBar):
if discCnt == 1:
print(f'{discCnt}disc: {fromBar}에서 {toBar}(으)로 이동!')
else:
moveDisc(discCnt-1, fromBar, viaBar, toBar) # (discCnt-1)개들을 경유 기둥으로 이동
print(f'{discCnt}disc: {fromBar}에서 {toBar}(으)로 이동!') # discCnt을 목적 기둥으로 이동
moveDisc(discCnt-1, viaBar, toBar, fromBar) # (discCnt-1)개들을 도착 기둥으로 이동
#2. 3개의 원판을, 1번 출발기둥 부터 시작해서, 3번 도착기둥 까지 옮기겠다, 경유 기둥은 2번 이다
moveDisc(3, 1, 3, 2)▼
1disc: 1에서 3(으)로 이동!
2disc: 1에서 2(으)로 이동!
1disc: 3에서 2(으)로 이동!
3disc: 1에서 3(으)로 이동!
1disc: 2에서 1(으)로 이동!
2disc: 2에서 3(으)로 이동!
1disc: 1에서 3(으)로 이동!14. 병합정렬
자료구조를 분할하고 각각의 분할된 자료구조를 정렬한 후 다시 병합하여 정렬한다
- 분할 시 : 각 숫자를 나눔
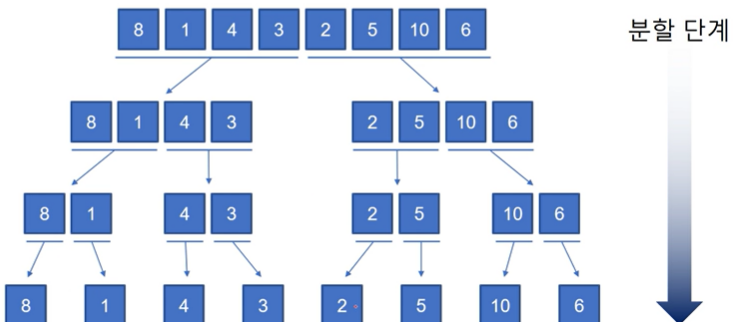
- 병합 시 : 각 옆의 숫자와 순서를 확인해 가장 작은 숫자부터 왼쪽 -> 오른쪽으로 나열
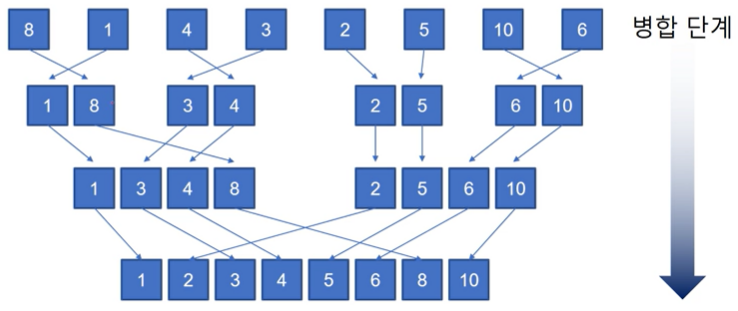
- 재귀함수 이기 때문에, 계속 분할(#2)하는 과정이 먼저 이뤄 짐
- return 된 뒤 병합 단계(#10)로 넘어 감
- 이후 크고 작음을 판별(#14)한 뒤 자리를 바꿈(#16)
-> 최종 정렬 완료 후 출력
def mSort(ns): #1. ns로 숫자를 받음
#2. ▼ 분할 단계
if len(ns) < 2: #3. ns의 길이가 2보다 작다면 (=1개만 남았다면)
return ns #4. ns 반환
midIdx = len(ns) // 2 #5. midIdx (중간값) = 전체 숫자 나열의 1/2
# 6. ▼ 재귀함수 이용
leftNums = mSort(ns[0:midIdx]) #7. 왼쪾 숫자 나열 = mSort호출 (0 부터 midIdx 전까지) ★
rightNums = mSort(ns[midIdx:len(ns)]) #8. 오른쪽 숫자 나열 = mSort호출 (midIdx 부터 끝까지) ★
# 9. ▲ 언제 까지 반복? : 1개가 남을 때까지( len(ns) < 2: ) 계속 분할한다..!!!!
# 10. ▼ 병합 단계
mergeNums = [] #11. 담을 리스트 만들어주기
leftIdx = 0 #12. 왼쪽
rightIdx = 0 #13. 오른쪽
#14. ▼ 병합 중, 크고 작음을 비교
#15. leftIdx가 leftNums보다 작고, rightIdx이 rightNums 보다 작다면
while leftIdx < len(leftNums) and rightIdx < len(rightNums):
#16. ▼ 자리 바꾸는 문장
if leftNums[leftIdx] < rightNums[rightIdx]:
mergeNums.append(leftNums[leftIdx])
leftIdx += 1
else:
mergeNums.append(rightNums[rightIdx])
rightIdx += 1
#17. 기존 값에 (시작 인덱스 ~ 끝)까지 더해준다
mergeNums = mergeNums + leftNums[leftIdx : ]
mergeNums = mergeNums + rightNums[rightIdx : ]
return mergeNums
nums = [0,1,4,3,2,5,10,6]
print(f'mSort(nums) : {mSort(nums)}')▼
mSort(nums) : [0, 1, 2, 3, 4, 5, 6, 10]🏷️실습

- sort.py
def mSort(ns, asc=True): ⭐ #1. 내림/오름 선택 & asc
if len(ns) < 2:
return ns
midIdx = len(ns) // 2
leftNums = mSort(ns[0 : midIdx], asc=asc) ⭐
rightNums = mSort(ns[midIdx : len(ns)], asc=asc) ⭐
mergedNums = []
leftIdx =0
rightIdx =0
while leftIdx < len(leftNums) and rightIdx < len(rightNums):
if asc:
if leftNums[leftIdx] < rightNums[rightIdx]:
mergedNums.append(leftNums[leftIdx])
leftIdx += 1
else:
mergedNums.append(rightNums[rightIdx])
rightIdx += 1
else:
if leftNums[leftIdx] > rightNums[rightIdx]:
mergedNums.append(leftNums[leftIdx])
leftIdx += 1
else:
mergedNums.append(rightNums[rightIdx])
rightIdx += 1
mergedNums = mergedNums + leftNums[leftIdx : ]
mergedNums = mergedNums + rightNums[rightIdx : ]
return mergedNums- ex.py
import random as rd
import sortMod as sm
#2. 랜덤 모듈로 1 ~ 100 까지, 10가지 수 발생 시킴
rNums = rd.sample(range(1, 101), 10)
print(f' not sorted rNums : {rNums}')
print(f'sorted rNums Asc 오름차순 : {sm.mSort(rNums)}') ⭐
print(f'sorted rNums Dsc 내림차순 : {sm.mSort(rNums, asc=False)}') ⭐▼
not sorted rNums : [30, 78, 60, 92, 54, 49, 99, 59, 40, 26]
sorted rNums Asc 오름차순 : [26, 30, 40, 49, 54, 59, 60, 78, 92, 99]
sorted rNums Dsc 내림차순 : [99, 92, 78, 60, 59, 54, 49, 40, 30, 26]15. 퀵 정렬
기존 값 보다 작은 값과 큰 값으로 분리한 구 다시 합친다
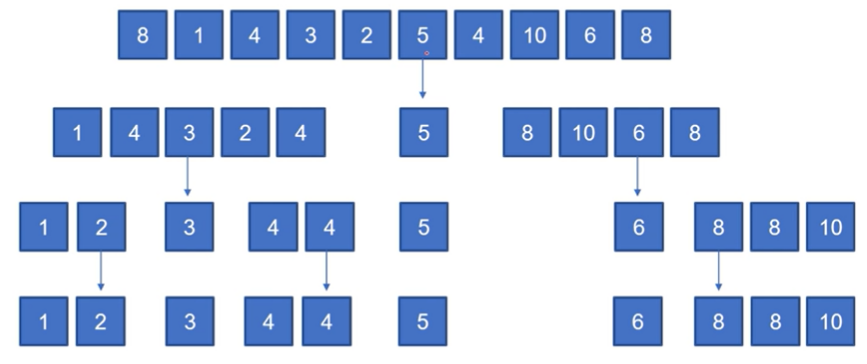
- 5를 기준으로 왼/오 를 나눔
- 왼쪽 3을 기준으로 왼/오 나눔
- 오른쪽 6을 기준으로 다 크니까, 모두 오른쪽으로 보냄
- 오른쪽 8을 기준으로 10을 오른쪽으로 보냄
-> 결과 적으로 오름차순으로 잘 정리 됨
def qSort(ns):
if len(ns) < 2:
return ns
midIdx = len(ns) // 2 #1. 기준 값
midVal = ns[midIdx]
smallNums = [] # 왼쪽 숫자 정렬
sameNums = [] # 그중 값이 같은 애들
bigNums = [] # 오른쪽 숫자 정렬
for n in ns:
if n < midVal: # 기준값 보다 작다면
smallNums.append(n) # 왼쪽에 추가
elif n == midVal: # 같다면
sameNums.append(n) # 같은수 리스트에 추가
else: # 큰경우,
bigNums.append(n) # 오른쪽에 추가
# 모든 값을 반환해줘야 함
return qSort(smallNums) + sameNums + qSort(bigNums)
nums = [0,1,4,3,2,5,4,10,6,8]
print(f'qSort(nums) :{qSort(nums)}')▼
qSort(nums) :[0, 1, 2, 3, 4, 4, 5, 6, 8, 10]🏷️실습

- sortMod.py
def qSort(ns, asc=True):
if len(ns) < 2:
return ns
midIdx = len(ns) // 2
midVal = ns[midIdx]
smallNums = []
sameNums = []
bigNums = []
for n in ns:
if n < midVal:
smallNums.append(n)
elif n == midVal:
sameNums.append(n)
else:
bigNums.append(n)
if asc: # 오름차순이 True이면 아래처럼 가고
return qSort(smallNums, asc=asc) + sameNums + qSort(bigNums, asc=asc)
else: # 내림차순 이면 아래와같이 해라
return qSort(bigNums, asc=asc) + sameNums + qSort(smallNums, asc=asc)- quickEx.py
import random as rd
import sortMod as sm
rNums = rd.sample(range(1,100), 10)
print(f'not sorted eNums: {rNums}')
print(f' sorted eNums ASC 오름차순 : {sm.qSort(rNums)}')
print(f' sorted eNums DSC 내림차순 : {sm.qSort(rNums, asc=False)}')▼
not sorted eNums: [94, 76, 97, 35, 49, 75, 80, 44, 67, 65]
sorted eNums ASC 오름차순 : [35, 44, 49, 65, 67, 75, 76, 80, 94, 97]
sorted eNums DSC 내림차순 : [97, 94, 80, 76, 75, 67, 65, 49, 44, 35]