최근에 경험을 위해 코딩테스트를 보고있는데, 트리를 이론으로만 공부해서 문제는 이해하지만 건들 수도 없었다.
그래서 트리를 공부하기 시작했다.
트리 순회
- Pre-order Traversal (전위 순회)
- In-order Traversal (중위 순회)
- Post-order Traversal (후위 순회)
- Level-order Traversal (레벨 순회)
순회에는 이렇게 4가지 종류가 있다.
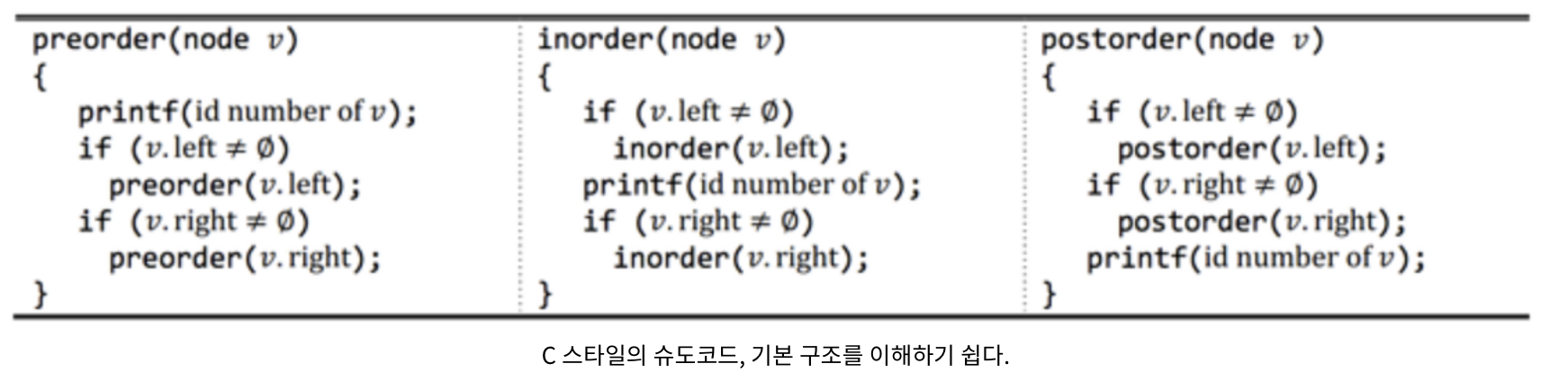
Pre-order
전위 순회는 Root -> Left -> Right 순으로 진행한다.
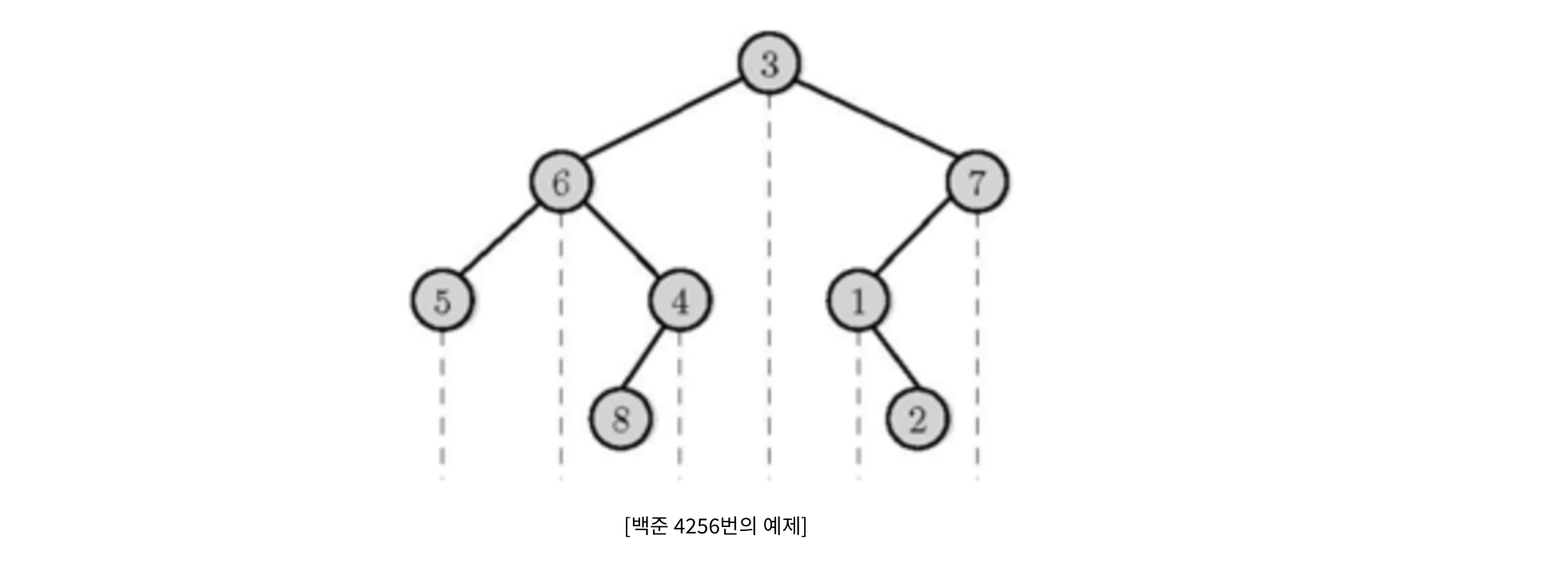
위의 예제을 전위 순회하면 3,6,5,4,8,7,1,2 이다.
트리 순회의 기초를 익히기 위해 리트 코드의 문제를 풀이해보았다.
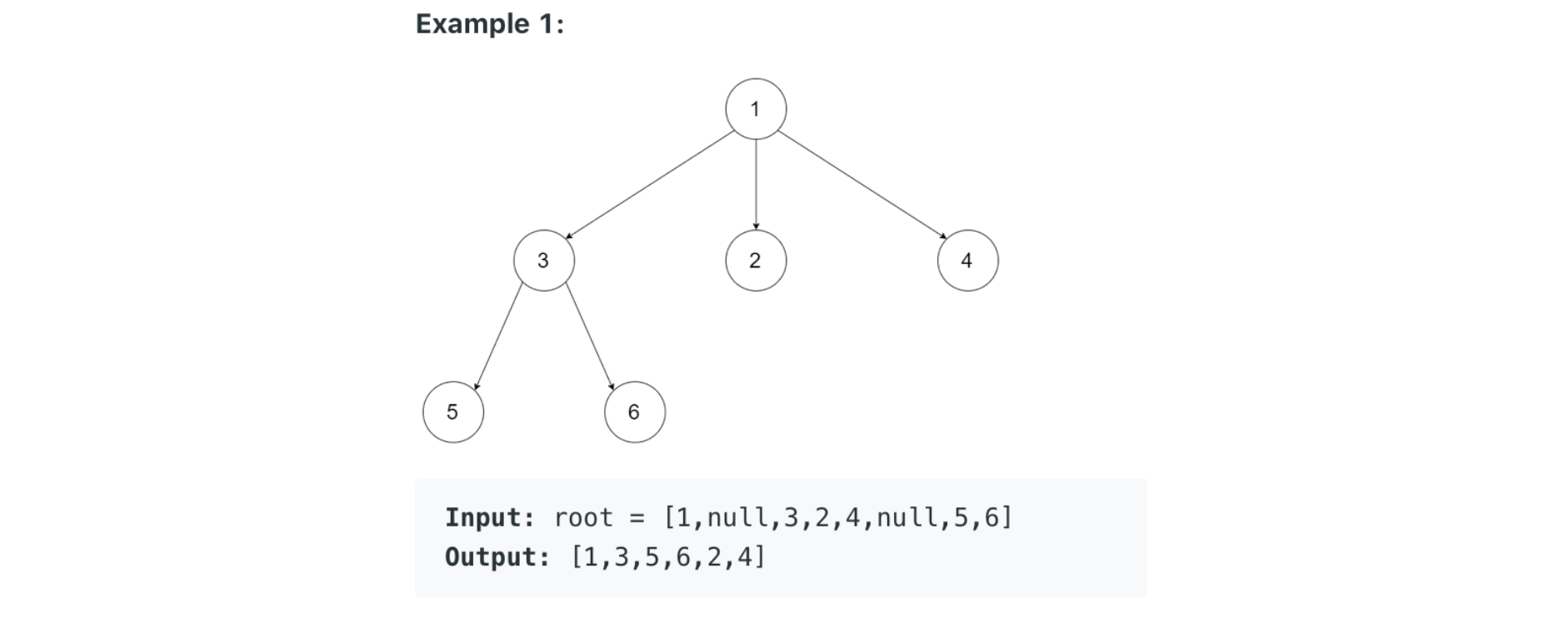
589. N-ary Tree Preorder Traversal
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
List<Integer> result = new ArrayList<>();
public List<Integer> preorder(Node root) {
if(root == null) return new ArrayList<Integer>();
result.add(root.val);
if(root.children != null) {
for(Node node : root.children) {
preorder(node);
}
}
return result;
}
}특이점이라면, 일반적인 트리 문제 풀이에서 주로 아래와 같은 구조의 클래스를 사용했는데, 위 문제에서는 자식을 List로 구현했다.
public class Node{
int val;
Node left;
Node right;
Node(int val) {
this.val = val;
}
}자식 노드를 별도의 노드로 연결해줬다면, Root -> Left -> Right 순이기 때문에, Left를 우선적으로 재귀호출 했을텐데 List의 형태이기 때문에 List의 인덱스 순서가 빠를 수록 왼쪽에 있는 것으로 for문으로 List의 원소를 꺼내고 꺼내는 데로 재귀를 호출한다.
In-order
중위 순회는 Left -> Root -> Right 순으로 진행 한다.
위 예제를 중위 순회하면 5,6,8,4,3,1,2,7이 된다.
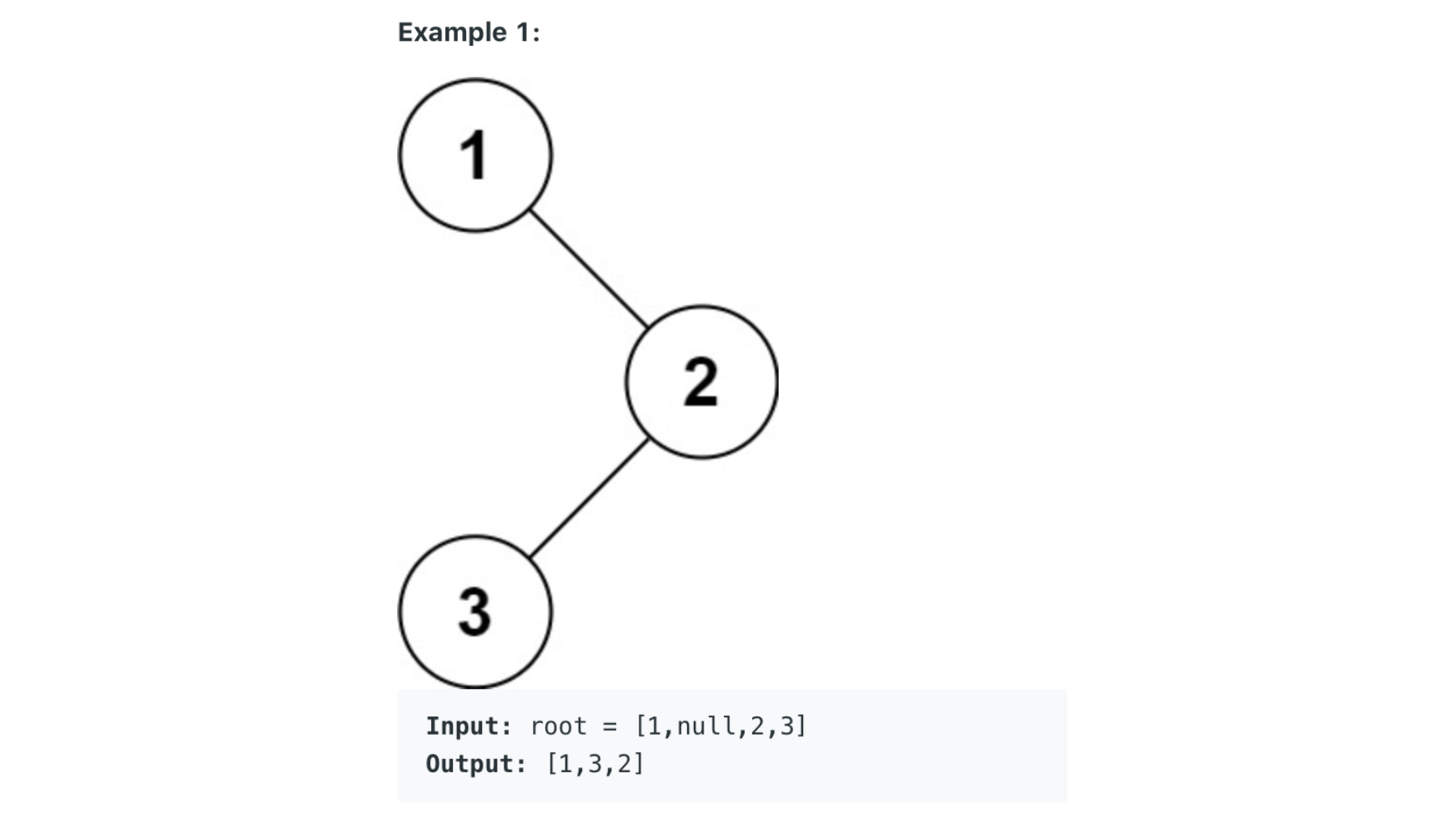
94. Binary Tree Inorder Traversal
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> result = new ArrayList<>();
public List<Integer> inorderTraversal(TreeNode root) {
if(root == null) return new ArrayList<Integer>();
if(root.left != null) inorderTraversal(root.left);
result.add(root.val);
if(root.right != null) inorderTraversal(root.right);
return result;
}
}위 문제는 나에게 익숙한 형태로 노드 클래스가 선언되어 있다.
Left -> Root -> Right 의 순서에 맞춰 조건문 짜준다.
Post-order
후위 순환은 Left -> Root -> Rightt순으로 진행한다.
위 예제를 후위 순환하면 5,8,4,6,2,1,7,3이 된다.
처음 봤을때 1보다 2가 먼저 나오는 것에 대해 좀 당황 스러웠다.
모든 순환은 순환 과정의 현재 노드를 루트 노드인 서브 트리로 보고,
순환을 진행 하므로 위 예제에서 왼쪽의 순환을 끝내고 오른쪽으로 넘어 왔을 때,
루트 노드가 1인 서브트리를 순환할 때, Left -> Right -> Root 순이기 때문에 Left(null) -> Right(2) -> Root(1) 순으로 순환하게 된다.
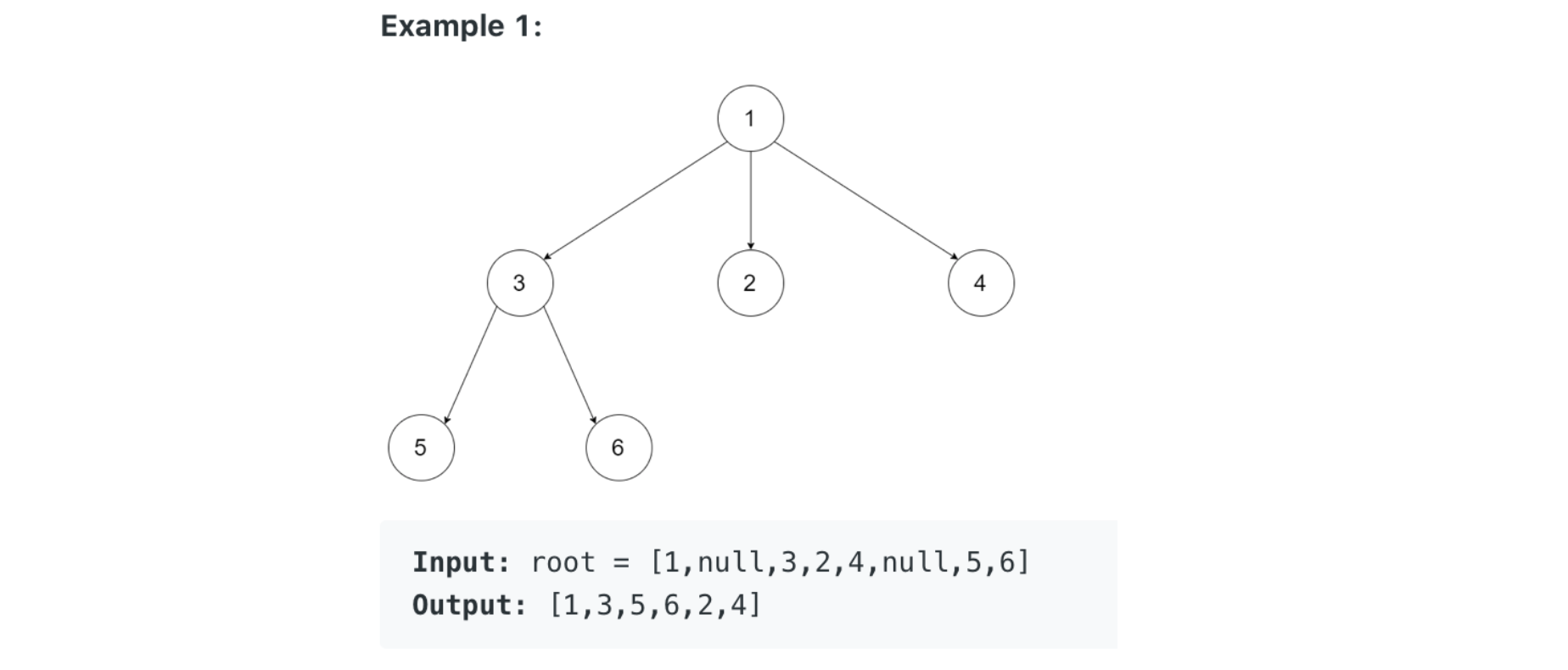
590. N-ary Tree Postorder Traversal
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public List<Integer> postorder(Node root) {
ArrayList<Integer> result = new ArrayList<>();
if(root == null) return result;
for(Node node : root.children) {
result.addAll(postorder(node));
}
result.add(root.val);
return result;
}
}코드의 구조를 보면 알겠지만, List로 연결 되어 있으면,
자식 노드를 가장 깊게 들어가면 된다.
이후 최고 레벨의 노드로 가게되면 Left -> Right -> Root 순이므로 List의 인덱스 순으로 순환을 하면 된다.
전위, 중위, 후위 순환의 코드를 보면 알 수 있듯이 전체 구조는 거의 비슷하고,
원하는 순환의 순환 우선순위에 따라 약간의 변형을 해주면 된다.
Level-order
레벨 순회는 계층의 레벨 별로 탐색을 진행한다.
위의 예제을 레벨 순회하면 3,6,7,5,4,1,8,2 이다.
개념 자체는 가장 쉬울 것이다.
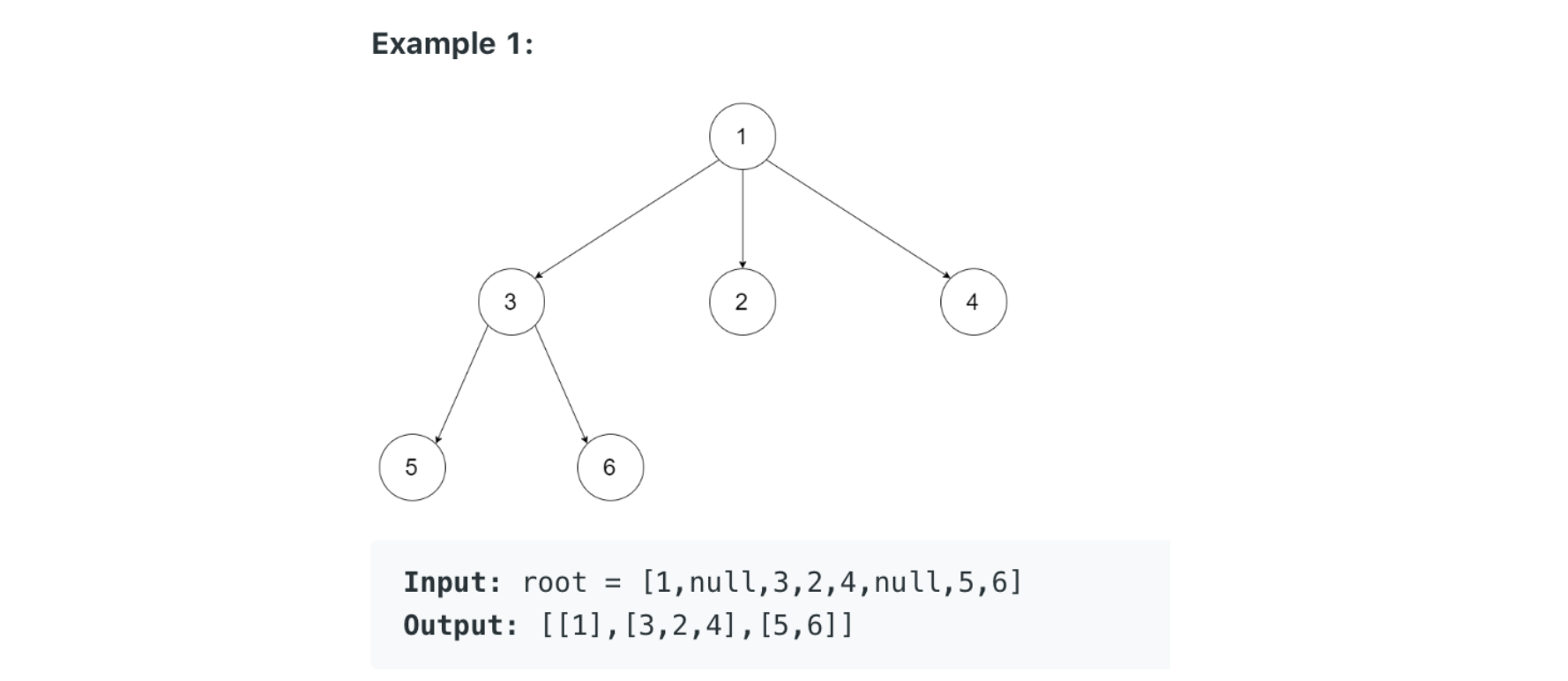
429. N-ary Tree Level Order Traversal
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) {
return result;
}
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
List<Integer> list = new ArrayList<>();
int size = queue.size();
for (int i = 0; i < size; i++) {
Node node = queue.poll();
list.add(node.val);
if (node.children != null) {
for (Node n : node.children) {
queue.add(n);
}
}
}
result.add(list);
}
return result;
}
}위 문제도 자식노드가 List로 연결되어있다.
레벨 순환은 특이하게 다른 순환들과 다르게 재귀로 순환하지 않는다.
처음에 문제를 풀이할 때, 재귀적으로 레벨을 올려가며 풀이하려고 했는데,
깔끔하지 않아서 찾아보니 Queue를 사용하여 BFS처럼 할 수 있음을 알게 되었다.
while문의 수행 횟수가 레벨의 수이다.
트리 순회의 특징
위 예제의 순회 결과를 살펴 보면
Pre : 3,6,5,4,8,7,1,2
In : 5,6,8,4,3,1,2,7
Post : 5,8,4,6,2,1,7,3
의 결과를 볼 수 있다.
이와 같은 결과가 있을 때, In + Post -> Pre, In + Pre -> Post를 할 수 있다.
package tree;
import java.io.*;
import java.util.*;
public class Q4256 {
static int[] pre, in;
static int n;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
StringTokenizer s;
while(t-- > 0) {
n = Integer.parseInt(br.readLine());
pre = new int[n];
in = new int[n];
s = new StringTokenizer(br.readLine());
for(int i = 0; i < n; i++) pre[i] = Integer.parseInt(s.nextToken());
s = new StringTokenizer(br.readLine());
for(int i = 0; i < n; i++) in[i] = Integer.parseInt(s.nextToken());
post(0, n, 0, sb);
sb.append('\n');
}
System.out.println(sb);
}
public static void post(int start, int end, int cur, StringBuilder sb) {
for(int i = start; i < end; i++) {
if(in[i] == pre[cur]) {
post(start, i, cur + 1, sb);
post(i + 1, end, cur + 1 + i - start, sb);
sb.append(pre[cur]).append(' ');
}
}
}
}
Pre는 Root -> Left -> Right순으로 순회하므로 첫 번째 원소가 전체 트리의 루트 노드이다.
In은 Left -> Root -> Right 순으로 순회하므로 전체 트리의 루트 노드를 알면 전체 노드중 왼쪽 서브 트리와 오른쪽 서브 트리를 구분할 수 있다.
Pre를 통해 알아낸 루트 노드와 In을 비교하여 서브트리를 구분 하고,
해당 서브트리의 루트 노드를 알아내어 서브트리를 계속 나누어서 Post를 알아낼 수 있다.
package tree;
import java.io.*;
import java.util.*;
public class Q2263 {
static int[] post, in;
static int n;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
StringTokenizer s;
n = Integer.parseInt(br.readLine());
in = new int[n];
post = new int[n];
s = new StringTokenizer(br.readLine());
for(int i = 0; i < n; i++) in[i] = Integer.parseInt(s.nextToken());
s = new StringTokenizer(br.readLine());
for(int i = 0; i < n; i++) post[i] = Integer.parseInt(s.nextToken());
pre(0, n, n-1, sb);
System.out.println(sb);
}
public static void pre(int start, int end, int cur, StringBuilder sb) {
for(int i = start; i < end; i++) {
if(in[i] == post[cur]) {
sb.append(post[cur]).append(' ');
pre(start, i, cur - end + i, sb);
pre(i + 1, end, cur - 1, sb);
}
}
}
}
위 알고리즘을 동일하게 사용한 In + Post -> Pre 문제이다.
그런데 문제는..

엄청난 시간이 걸렸다. for문을 계속 돌려서 비교하다보니 노드의 수가 10만개 까지 들어와서 엄청나게 걸렸다..
이 시간을 줄일 수 있는 방법을 찾아봐야겠다.
https://pangsblog.tistory.com/47
이 분께서 각 인덱스를 배열에 저장해서 for문을 돌려 검색하는 시간을 없애셨다.
알고리즘 자체는 동일 했다. 참고하면 좋을듯..
