자료구조

• 선형구조: list
• 비선형구조: tree

linked list에서 탐색의 경우, 최악은 O(n). 탐색을 head에서부터 해야 하므로 임의의 장소로 바로 갈 수 없다.

자료구조를 선택할 때 고려할 것

1. 무엇을 저장하는가
2. 동작시간은 어느정도여야 하는가
3. memory 사용량은 어느정도여야 하는가
4. 구현은 얼마나 편리한가

---

Tree

개요

기본적인 tree의 용어 및 구조에 대해 확인하고 binary tree와 binary search tree에 대해 학습한다.

트리를 왜 사용하는가?

선형구조인 list에 비해 탐색시간이 절감된다는 큰 장점이 있다.

용어(terminology)

• node, edge, root, subtree, child

• sibling: 같은 level의 children

• leaf: child가 없는 노드

• ancester: 특정 노드로부터 root까지 올라가며 존재하는 모든 노드

• decendent: subtree의 모든 것
  

• Depth of x
  : length of path from root to x (root에서부터 x까지의 path 수)
  : number of edges in path from root to x (root에서부터 x까지의 path에 있는 간선의 수)

• height of x
  : number of edges in logest path from x to leaf (x에서부터 leaf노드까지의 가장 긴 path에 있는 간선의 수)

---

1. Binary Tree(이진트리)

: children을 최대 2개까지만 가질 수 있는 tree

• 0~2개의 자식만을 가질 수 있다.
• left child와 right child를 구분한다.
• leaf 노드는 null을 가리킨다.(memory가 낭비되지만 탐색속도를 위해 희생)
  

## 이진트리 구현 1) 동적 노드 생성 ``` Struct Node{ int data; struct Node * left; struct Node * right; } ``` 2) 배열로 생성  index 0의 child: index 1, index 2 index 1의 child: index 5, index 8 - index i의 left child: 2i+1, right child: 2i+2 - 배열 생성의 장점: 메모리 사용량이 줄고 인덱스로 접근하여 탐색 속도가 빠르다. - 배열 생성의 단점: 동적 데이터 삽입/삭제의 경우에 좋지 않다.

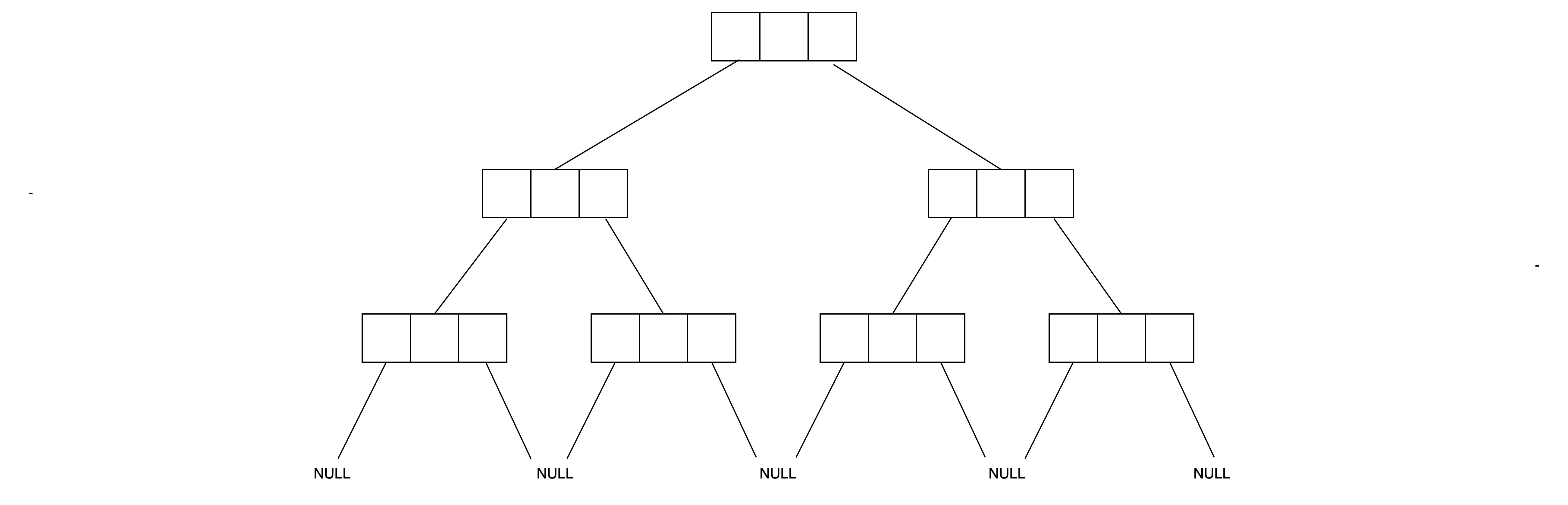
1-1. Complete Binary Tree(완전이진트리)

: 마지막 level을 제외하고 모든 level이 완전히 채워지고, 만약 채워지지 않았다면 모든 노드들이 왼쪽부터 채워진 트리

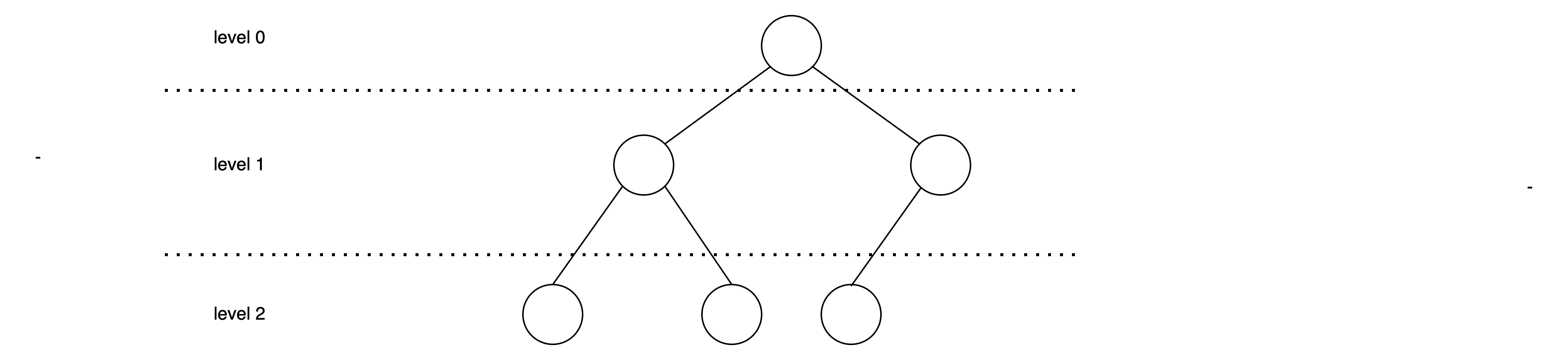
• 가장 마지막 level이 안 채워졌다면, 왼쪽부터 채워져있어야 한다.

1-2. Perfect Binary Tree(포화이진트리)

: 마지막 level까지 모든 노드가 2개의 자식을 가지는 트리

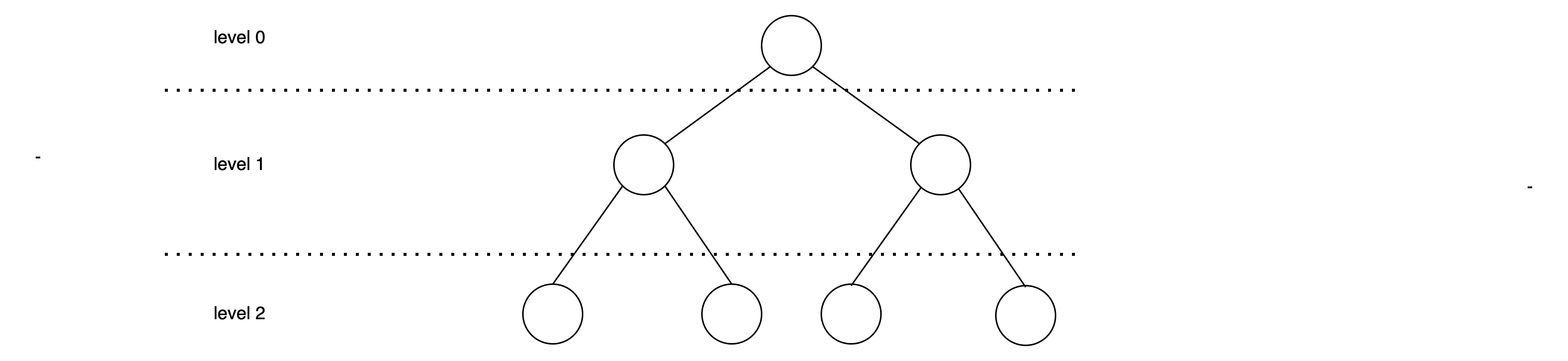
• h = log(n+1)-1 (여기서 log의 밑은 2, h는 높이, n은 노드 수를 의미)

1-3. Balanced Binary Tree

: 모든 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 k보다 크지 않은 트리 (보통 k=1)

• h가 작을수록 탐색 속도가 짧으므로 탐색 속도가 빠름

---

2. Binary Search Tree(BST, 이진탐색트리)

• 이진탐색트리는 탐색, 삽입, 삭제 모두 O(log n)으로 빠르다.
• key에 대해 left subtree < right subtree이다.
• left subtree엔 root의 key 값보다 작은 값들만이 존재하고, right subtree엔 root의 key값보다 큰 값들만 존재한다.
• subtree의 root에 대해서도 동일하게 적용된다.
• 입력되는 순서에 따라, balanced가 지켜지지 않을 수 있다.

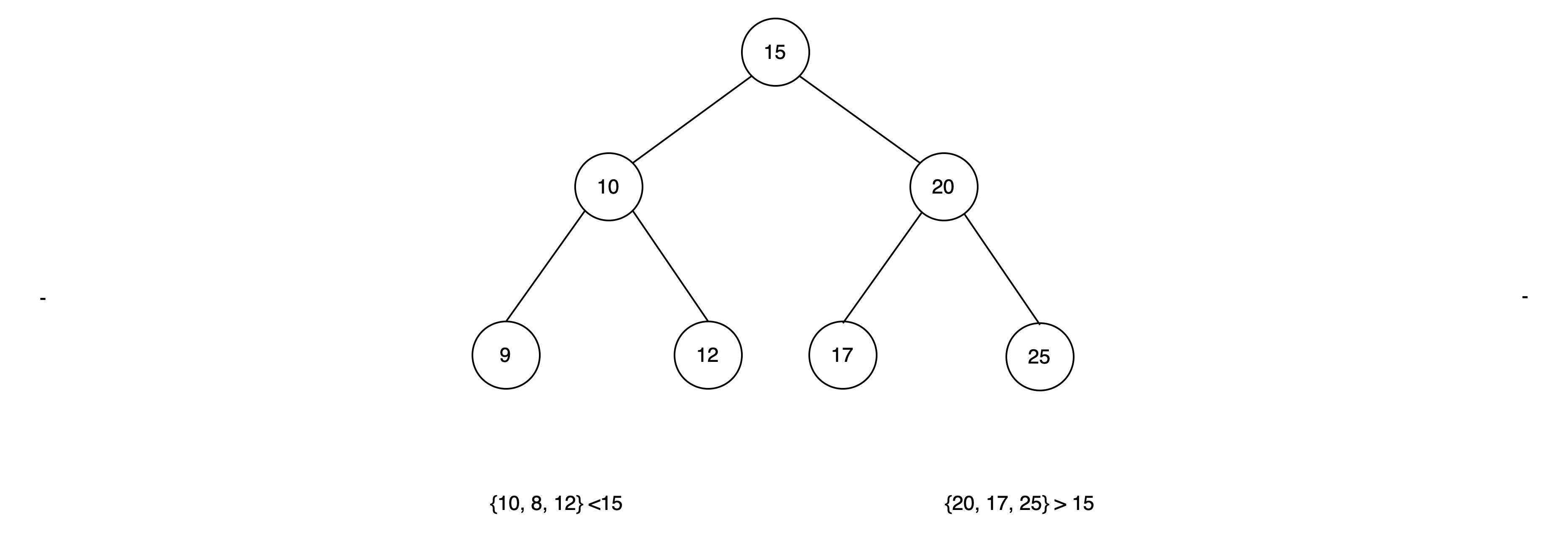
이진트리와 이진탐색트리의 차이

	이진트리	이진탐색트리
search, insert, remove	배열(정렬x) O(n), O(1), O(n) 연결리스트 O(n), O(1),O(n) 배열(정렬o) O(log n), O(n), O(n)	O(log n)
정렬여부	X	O

이진탐색트리 구현

• Double linked list이용

Strucnt BSTNode{
	int data;
    BSTNode* left;
    BSTNode* right;
}

BSTNode* Insert(BSTNode* root, int data){
	if(root==NULL){
    	root = GetNewNode(data);
    }else if(data <= root->data){
    	root->left = Insert(root->left, data);
    }else{
    	root->right = Insert(root->right, data);
    }
    return root;
}

int Search(BSTNode* root, int data){
	if(root == NULL) return 0;
    else if(root-> data == data) return 1;
    else if(root->data >= data) return Search(root->left, data);
    else return Search(root->right, data);
}

int main(){
	BSTNode* rootPtr;
    root = Insert(0,15);
    root = Insert(root,10); 
    root = Insert(root,20);
    .
    .
    .
    num입력받기
    if(Search(root, num) == 1) Printf('found');
}

자세히 살펴보자.

//main
	root = Insert(0,15);

main의 다음 코드에 따라 Insert 함수를 호출한다.

BSTNode* Insert(BSTNode* root, int data){
	if(root==NULL){ 
    	root = GetNewNode(data);
    }else if(data <= root->data){
    	root->left = Insert(root->left, data);
    }else{
    	root->right = Insert(root->right, data);
    }
    return root;
}

Insert의 첫 if문으로 들어가며 다음과 같은 상태가 된다.

//main
	root = Insert(root,10); 

root가 200을 가리키고 data(10)이 root의 data(15)보다 작으므로 else if 로 진입한다.
else if 내의 순환으로, Insert(0, 10)을 호출하고 root->left가 그를 가리킨다.

---

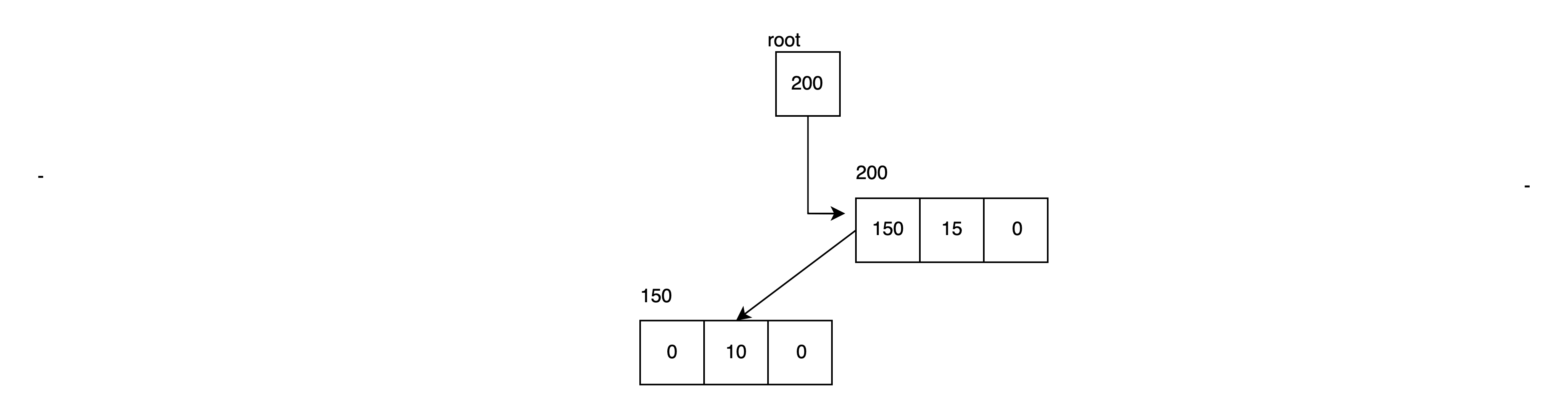
BST 최소값, 최대값 찾기

• 정렬되어있는 BST는 최소값, 최대값 찾기에 적합
• BST에서 최소값은 좌측 끝에 존재하고 최대값은 우측 끝에 존재한다.

최소값 찾기 (FindMin)

//current선언
int FindMin(BSTNode * root){
	if(root == NULL){
    	printf("error, Empty"); 
        return -1;
    }
	BSTNode* current = root;
    while(current->left != NULL){
    	current = current->left;
    }
    return current->data;
}

또는 

//current선언없이, root를 바로 사용해도 된다. 파라미터 root는 함수 내에 있는 지역변수이므로
int FindMin(BSTNode * root){
	if(root == NULL){
    	printf("error, Empty"); 
        return -1;
    }
    while(root->left != NULL){
    	root = root->left;
    }
    return root->data;
}

//순환호출 사용하기
int FindMin(BSTNode * root){
	if(root == NULL){
    	printf("error, Empty"); 
        return -1;
    }else if(root->left == NULL){
    	return root->data;
    }
    return FindMin(root->left);
}

최대값 찾기 (FindMax)

//current선언
int FindMax(BSTNode * root){
	if(root == NULL){
    	printf("error, Empty"); 
        return -1;
    }
	while(root->right != NULL){
    	root = root->right;
    }
    return root->data;
}

---

이진탐색트리 최대 높이 구하기

• height : # of edges in logest path from root to leaf node
• 반복문과 재귀함수를 이용하여 최대 높이를 구해본다.

cf.
depth: root에서 x까지의 높이
(height는 root에서 x를 거쳐 leaf까지의 높이)

int FindHeight(BSTNode* root){
	if(root == NULL) return -1;
    int leftHeight = FindHHeight(root->left);
    int rightHeight = FindHeight(root->right);
    return max(leftHeight, rightHeight) + 1;
}

최악은 O(n
보통......

---

이진탐색트리 순회

• 노드당 한번만 방문한다. 즉, 다시 방문하지는 않는다.

1. 넓이우선순회 (BFS, Breath First Search)
2. 깊이우선순회 (DFS, Depth First Search)

아래의 트리에 대해 1, 2번 순회를 확인한다.

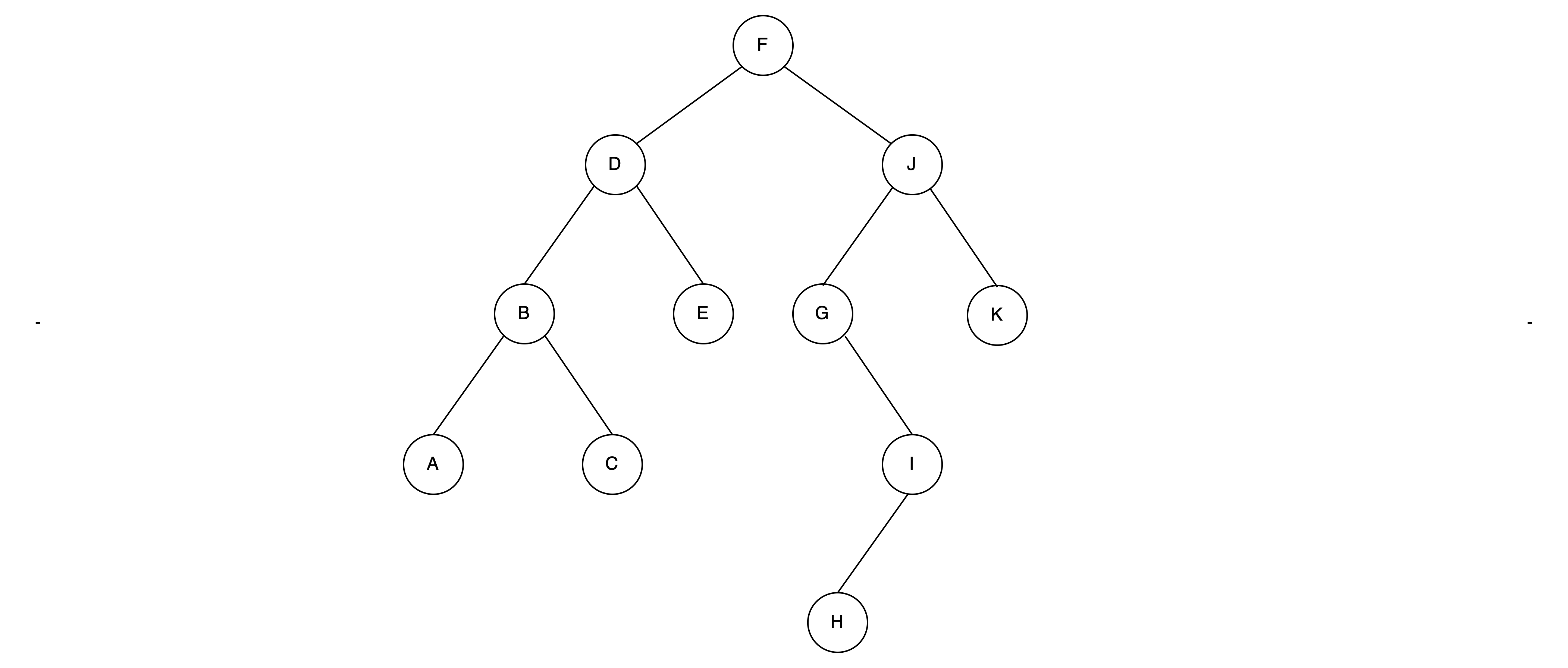
1. BFS(넓이우선순회)

• 왼쪽 먼저
• 낮은 level 먼저

레벨순서순회(level order traversal)

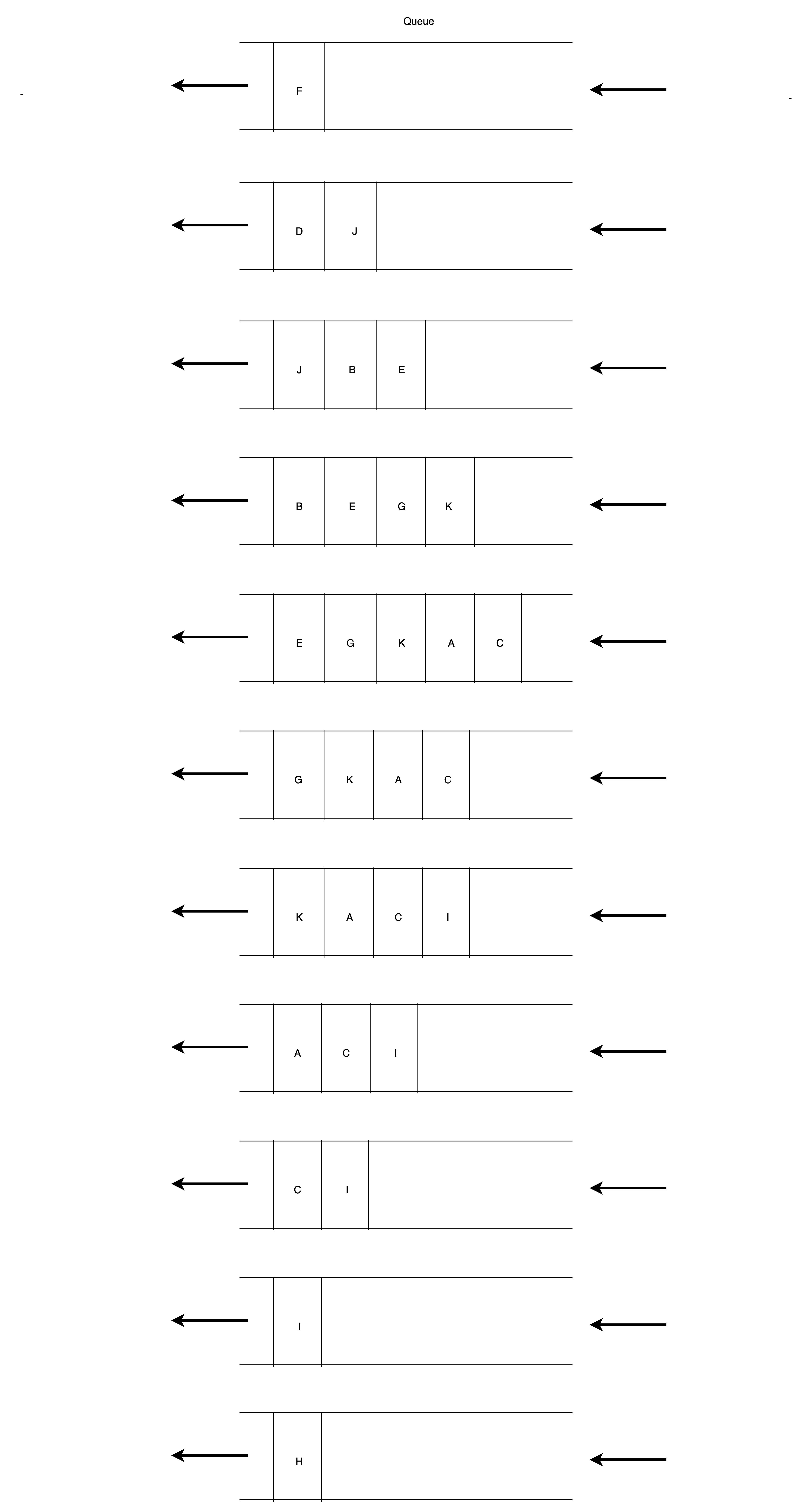
F -> D -> J -> B -> E -> G -> K -> A -> C -> I -> H 순으로 순회한다.

2. DFS(깊이우선순회)

• 3가지 방법으로 깊이우선순회할 수 있다. 순회하는 순서에 따라 (1) preorder; (2) inorder; (3) postorder로 나뉜다.
  

(1) preorder

root, left, right순으로 순회한다.
위의 트리에 대해, F -> D -> B -> A -> C -> E -> J -> G -> I -> H -> K 순으로 순회한다.

(1) inorder

left, root, right순으로 순회한다.
A -> B -> C -> D-> E -> F -> G -> H -> I -> J -> K

(1) postorder

left, right, root순으로 순회한다.
A -> C -> B -> E -> D -> H -> I -> G -> K -> J -> F

---

1. BFS 구현

ADT를 생각하고 구현한다.

• Queue에서 나가며 나가는 노드의 자식을 Queue에 넣는다.