
최소 신장 트리 알고리즘 (MST, Minimum Spanning Tree)
최소 신장 트리 (MST) 는 가중치가 있는 무방향 그래프에서 모든 노드를 포함하면서 가중치의 합이 최소가 되는 트리를 의미한다.
즉, 모든 정점을 연결하면서 최소의 가중치로 연결하는 그래프의 부분 그래프를 찾는 것이 목적이다.
MST의 특징
-
N개의 정점을 가지는 그래프에서 MST는 (N-1)개의 간선만을 가짐
-
사이클이 없어야 함 (트리 구조)
-
모든 정점이 연결되어 있어야 함 (연결 그래프)
-
가중치의 합이 최소여야 함
해결 방법
MST를 해결하는 방법은 크게 2가지 방법이 존재한다.
정점을 기준으로 확장하는 방법인 프림 알고리즘(Prim’s Algorithm), 간선을 기준으로 하는 크루스칼 알고리즘 (Kruskal’s Algorithm) 이렇게 두 방법이 존재한다.
1. 프림 알고리즘 (Prim's Algorithm)
프림 알고리즘은 간단하게 설명을 하면 시작점에서 노드를 Greedy Algorithm를 이용하여 추가하면서 확장하는 방법을 이용한다.
현재 위치의 노드에서 연결된 인접 노드들 중 가장 적은 비용의 간선을 추가하고, 추가된 노드들 중 가중치가 적은 간선을 선택하는 작업을 계속 진행한다.
트리 집합에 속한 정점들과 인접한 정점들 중 가장 낮은 가중치의 간선과 연결된 정점에 대해 간선과 정점을 MST 트리 집합에 포함한다.
사이클을 막기 위해 연결된 정점이 이미 트리가 속한다면 그 다음 순서를 넣는다.
해당 과정을 MST 집합의 원소 개수가 그래프의 정점의 개수가 될 때까지 반복한다.
(간선의 가중치를 더해서 최소 신장 트리 비용 산출)
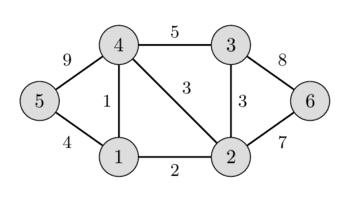
해당 그래프를 예를 들어서 풀어보자.
Step 1.
처음 시작점인 1을 기점으로 인접한 간선 중 가중치가 작은 간선을 선택하여 확장한다.
MST = {1, 4}, 가중치 : 1
Step 2.
현재 MST 집합의 원소는 1과 4가 있기 때문에 1, 4의 노드에서 가장 작은 가중치를 갖는 간선을 찾아 확장을 한다.
1-2의 가중치가 2로 다음으로 가장 작은 가중치를 갖기 때문에 이를 선택하여 확장한다.
MST = {1, 4, 2}, 가중치 : 3
Step 3.
MST = {1, 4, 2, 3}, 가중치 : 6
Result = 17
이렇게 위 과정을 반복하여 17의 가중치로 문제를 해결할 수 있다.
2. 크루스칼 알고리즘 (Kruskal's Algorithm)
프림 알고리즘은 현재 MST에 포함된 정점에서 가장 작은 가중치를 가진 간선을 선택해 확장하는 정점 중심 접근 방식이지만,
반면, 크루스칼 알고리즘은 전체 간선을 가중치 기준으로 정렬한 후, 작은 간선부터 선택하는 간선 중심 접근 방식이라는 점이 중요하다.
이번에는 다른 예시로 문제를 해결해보자.
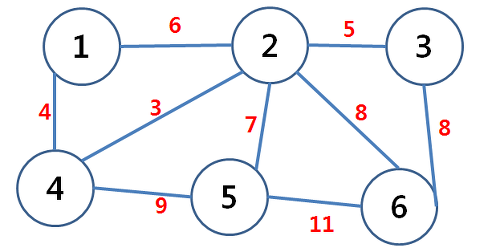
Step 1.
일단 가중치 기준으로 간선들을 정렬을 해야 해결이 편하다.
| 가중치 | 정점 1 | 정점 2 |
|---|---|---|
| 3 | 2 | 4 |
| 4 | 1 | 4 |
| 5 | 2 | 3 |
| 6 | 1 | 2 |
| 7 | 2 | 5 |
| 8 | 2 | 6 |
| 8 | 3 | 6 |
| 9 | 4 | 5 |
| 11 | 2 | 6 |
위 처럼 간선의 거중치를 기준으로 정렬을 했다면 이제 가장 작은 가중치를 선택하여 문젤제를 해결한다.
노드 2와 4를 연결하는 간선을 선택한다.
MST = {2, 4} 가중치 = 3
Step 2.
다음으로 작은 간선인 정점 1과 4의 간선을 선택한다.
MST = {2, 4, 1} 가중치 = 7
Step 3.
MST = {2, 4, 1, 3} 가중치 = 12
Step 4.
다음으로 가중치가 작은 간선은 6의 가중치를 갖는 노드1과 2의 간선이다.
하지만 해당 간선을 선택하면 사이클이 발생하기 때문에 해당 간선은 추가하지 않고 다음으로 넘어간다.
MST = {2, 4, 1, 3} 가중치 = 12
해당 과정을 반복하면 총 27의 가중치로 모든 노드들을 연결할 수 있다.
이렇게 최소 신장 트리 알고리즘(MST) 해결 방법에 대한 두가지 방법에 대해서 알아보았다.
