[알고리즘] - 계산 기하학

🧐 계산 기하 알고리즘??

컴퓨터 과학과 수학에서 사용되는 알고리즘의 한 부분이다.
기하학적인 문제 해결을 하는 데 주로 사용이 된다.
(점, 선, 다각형과 원 등 기하학적 도형을 다룬다)

2차원과 3차원의 도형을 다루는 주제이지만, 2차원 기하학만을 다루겠다.

백터란?

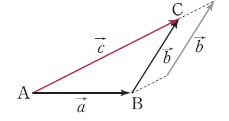
벡터는 두 점의 상대적인 위치 표현을 하기 위해서 사용하는 것이다.
2차원 백터는 성분 표시를 사용하여 ($x$ 좌표 차이, $y$좌표 차이) 형태로 표현할 수 있다.

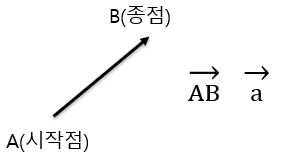
예를 들어 시작점의 좌표가$(1,1)$, 종점의 좌표가$(8,3)$이라고 가정을 할 때, 점 $A$에서 점 $B$를 향하는 백터의 성분 표시는 $(7,2)$가 된다.

일반적으로 점 $A$에서 점 $B$로 향하는 백터를 $\overrightarrow{AB}$ 라고 표시를 하며 $\overrightarrow{AB}=(7,2)$처럼 성분 표시를 한다. 또한 백터는 $\overrightarrow{a}$, $\overrightarrow{b}$처럼 하나의 문자를 사용하여 표현 하기도 한다.

백터는 크기와 방향을 갖는 양이라고 이야기 할 수 있으며,
크기와 방향이 둘다 같으면 "같은 벡터이다"라고 말을 할 수 있다.

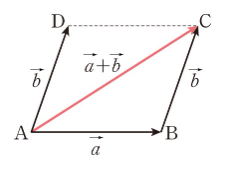
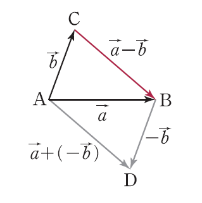
백터의 덧셈, 뺄셈

백터는 싱수와 같이 덧셈과 뺄셈이 가능하다. 백터 $\overrightarrow{a}$의 성분 표시를 $(a_x, a_y)$, $\overrightarrow{b}$의 성분 표시를 $(b_x, b_y)$이라고 할 때

• $\overrightarrow{a} + \overrightarrow{b} = (a_x+b_x, a_y+b_y)$
  
  

• $\overrightarrow{a} - \overrightarrow{b} = (a_x-b_x, a_y-b_y)$
  

백터의 크기

백터의 크기는 간단하게 말을하면 점 $A$에서 점 $B$까지의 화살표의 길이라고 이해를 하면 된다.
$|\overrightarrow{a}|,\overrightarrow{AB}$ 처럼 절댓값 기호를 붙여서 표현을 한다.

$|\overrightarrow{a}|=\sqrt{ {a_x}^2 + {b_y}^2}$

예를 들어서 점 $A$의 좌표가 $(1,1)$ 점 $B$의 좌표가 $(5,4)$라고 할 때
$|\overrightarrow{AB}|=5$가 된다.

백터의 내적

백터 $|\overrightarrow{a}|$의 성분 표시를 $(a_x,a_y)$, 백터 $|\overrightarrow{b}|$의 성분 표시를 $(b_x,b_y)$라고 할 때
내적 $\overrightarrow{a}·\overrightarrow{b}$는 $a_xb_y+a_yb_y$의 값이 된다.

여기서 $\overrightarrow{a}·\overrightarrow{b}$의 값이 $0$이라면 두 백터는 서로 수직이라는 것을 의미하고, 양수일 때는 $90°$ 보다 작고, 음수일 때 $90°$보다 크다.

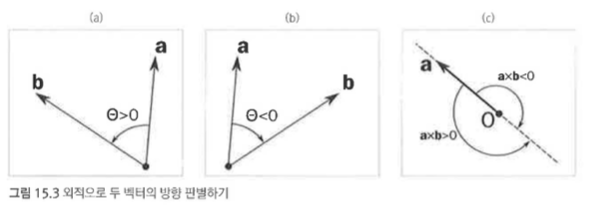
백터의 외적

외적은 원래 4차원 공간에서 정의된 것이지만, 2차원 평면 위의 백터도 외적의 크기를 계산할 수 있다.

백터의 외적 $|\overrightarrow{a}\times\overrightarrow{b}|=|a_xb_y-a_yb_x|$

여기서 기하학 알고리즘 구현에 있어서 중요한 부분이 있다.

• 외적의 크기는 2개의 백터가 만드는 평행사변형의 면적과 반드시 같다.
• 외적 식에서 절댓값을 제외한 $a_xb_y-a_yb_x$를 $cross(\overrightarrow{a},\overrightarrow{b})$라고 할 때
  점 $A,B,C$가 시계 방향으로 위치 한다면 $cross(\overrightarrow{a},\overrightarrow{b})$가 양수
  점 $A,B,C$가 반시계 방향으로 위치 한다면 $cross(\overrightarrow{a},\overrightarrow{b})$가 음수
  * 점 $A,B,C$가 일직선 위에 위치 한다면 $cross(\overrightarrow{a},\overrightarrow{b})$가 $0$이 된다.
  

예제

점과 선분의 거리

2차원 평면 위 점 $A, B, C$가 있다. 점 $A$의 좌표는 $(a_x,a_y)$, 점 $B$의 좌표는 $(b_x,b_y)$, 점 $C$의 좌표는 $(c_x,c_y)$라고 하자
그러면 "점 $A$"와 "선분$BC$ 위에 있는 점"으; 최단 길이를 구하라

이러한 문제가 주어질 때 앞에서 간단하게 다시 공부한 내용을 바탕으로 쉽게 해결이 가능하다.

백터의 내각과 각도의 관계 관련해서 확인을 했던 내용을 사용하면 된다.

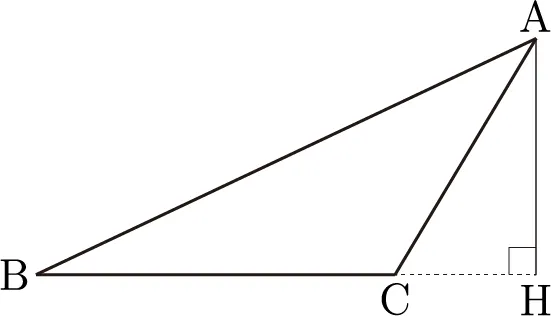
위 이미지를 삼각형이 아닌 점 $A,B,C$만 보면 된다.

만약 이러한 패턴일 경우 최단거리는 단순하게 $A$와 $C$의 거리가 된다.

하지만

위 이미지를 삼각형이 아닌 점 $A,B,C$만 보면 된다.

이러한 패턴일 경우 앞에서 확인했던 최단거리를 구하는 방법보다 좀 복잡하다.

점 $A$에서 선분 $BC$위로 수선의 발을 직각으로 내려 해당 거리를 반환을 해줘야 한다.

점 $A$에서 수선의 발 $H$ 사이의 거리를 구하는 방법으로 간단하게 $BA$와 $BC$를 사용하여 평행사변형을 생각하고, 해당 넓이를 $S$라고 할 때 $S$를 선분 $BC$로 나누면 간단하게 최단거리를 구할 수 있다.

$d=\frac{|\overrightarrow{BA}\times\overrightarrow{BC}|}{|\overrightarrow{BC}|}$

		Scanner sc = new Scanner(System.in);
		long ax = sc.nextInt(), ay = sc.nextInt();
		long bx = sc.nextInt(), by = sc.nextInt();
		long cx = sc.nextInt(), cy = sc.nextInt();
		
		// 벡터 BA, BC, CA, CB의 성분 표시를 구함
		long BAx = ax - bx, BAy = ay - by;
		long BCx = cx - bx, BCy = cy - by;
		long CAx = ax - cx, CAy = ay - cy;
		long CBx = bx - cx, CBy = by - cy;
		
		// 어떤 패턴에 해당되는지 판정
		int pattern = 2;
		if (BAx * BCx + BAy * BCy < 0L) {
			pattern = 1;
		}
		if (CAx * CBx + CAy * CBy < 0L) {
			pattern = 3;
		}
		
		// 점과 직선의 거리 구하기
		double answer = 0.0;
		if (pattern == 1) {
			answer = Math.sqrt(BAx * BAx + BAy * BAy);
		}
		if (pattern == 3) {
			answer = Math.sqrt(CAx * CAx + CAy * CAy);
		}
		if (pattern == 2) {
			double S = Math.abs(BAx * BCy - BAy * BCx);
			double BCLength = Math.sqrt(BCx * BCx + BCy * BCy);
			answer = S / BCLength;
		}

그 외 다른 문제

• $N$개의 점들이 주어질 때, 가장 가까운 두 점 사이를 구하는 문제도 해결이 가능하다.
  모든 쌍을 구해서 길이를 계산을 한다면 시간 복잡도는 $O(N^2)$가 될 것이다. 하지만 분할 정복법이라는 알고리즘과 같이 사용한다면 $O(NlogN)$으로 단축이 된다.

• 볼록 다각형 만들기
  $N$개의 점을 모두 포함하는 다각형 중 가장 작은 다각형을 구하는 문제가 있다. 해당 문제는 Andrew알고리즘을 사용하면 $O(NlogN)$이 된다.

• 보로노이 다이어그램 만들기
  $N$개의 점이 주어질 때 각각의 점이 지배하는 영역을 구하는 문제이다. 해당 문제는 지배하는 영역의 경계는 반드시 두 점의 수직 이등분선이 된다. 따라서 수직 이등분선을 전부 구하는 방법을 사용해 볼 수 있다.
  추가적으로 평면 주사라는 개념을 기반으로 만든 Fortune알고리즘을 사용하면 $O(NlogN)$시간으로 보로노이 다이어그램을 구할 수 있다.