[알고리즘] 그래프를 사용한 알고리즘

buckshot·2024년 5월 26일
BFSDFS그래프깊이 우선 탐색너비 우선 탐색

알고리즘

목록 보기
10/19
post-thumbnail

그래프란?

여러 대상을 연결하여 표현한 네트워크 구조를 그래프라고 표현을 한다. 즉, 네트워크 구조를 의미한다.

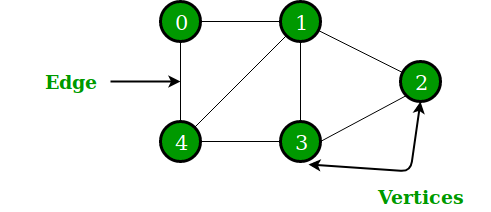
그래프는 정점(vertex)과 변(edge)으로 이루어진다.
정점은 대상을 나타내고, 변은 대상들의 관계를 나타낸다.

그래프의 종류

  • 무향 그래프, 유향 그래프

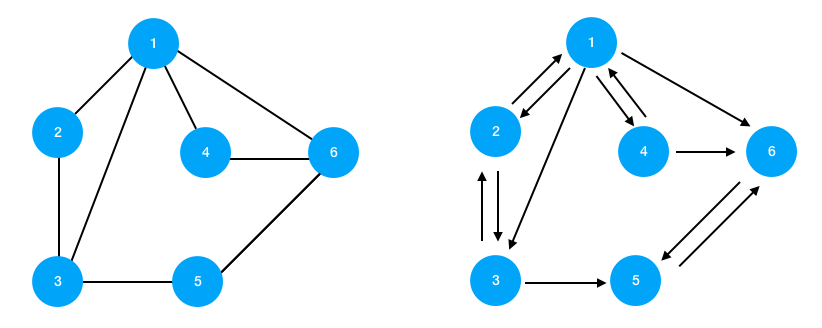
    • 무향 그래프 : 변에 방향 표시가 따로 없는 그래프
    • 유향 그래프 : 변에 방향 표시가 있는 그래프

  • 가중치 없는 그래프, 가중 그래프


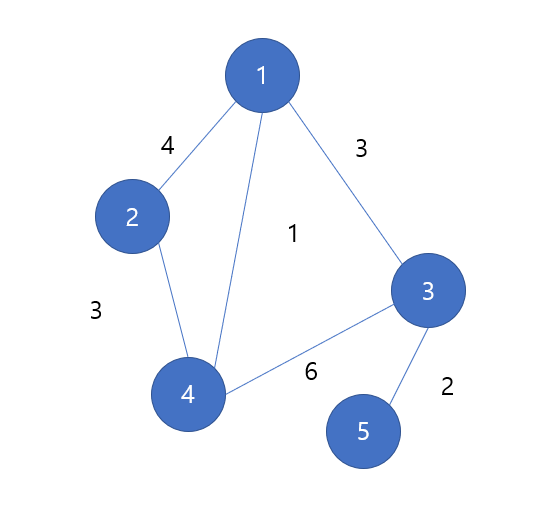
    위 처럼 변에 가중치가 있는 그래프를 가중 그래프라고 한다.

  • 이분 그래프


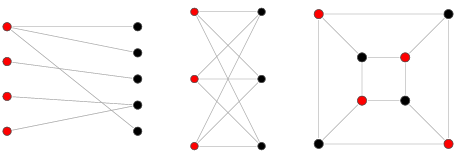
    직접적으로 변으로 연결된 정점끼리 같은 색이 되지 않게 두 가지 색상으로 나눠 칠할 수 있는 그래프를 이분 그래프라고 한다.

추가적으로 n가지 색으로 칠할 수 있는 그래프를 "n-채색 가능한 그래프"라고 한다.

  • 평면 그래프


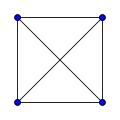
모든 변이 교차하지 않게 그릴 수 있는 그래프를 평면적 그래프라고 부른다.


모든 변이 실제로 교차하지 않게 그린 그래프를 평면 그래프라고 한다.

참고로 평면 그래프는 '변의 수가 정점 수의 3배보다 작고','4가지 색만으로 이웃한 정점이 같은 색이 되지 않게 칠할 수 있다(4색 정리)' 이러한 특징이 있다.

  • 연결 그래프, 비연결 그래프


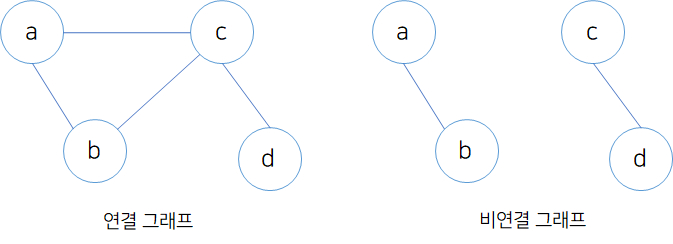
모든 정점에 대하여 경로가 존재하는 그래프를 연결 그래프, 모든 정점에 대하여 경로가 없는 경우 비연결 그래프라고 한다.

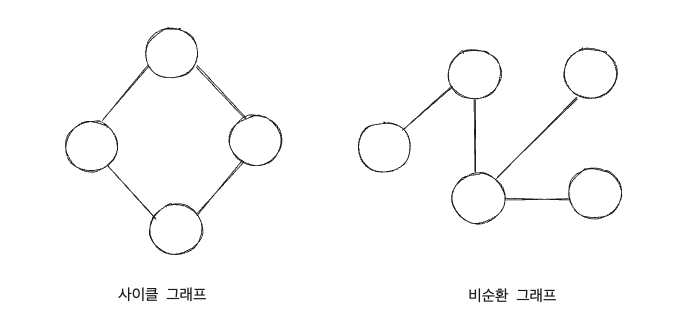
  • 사이클 그래프, 비순환 그래프

  • 오일러 그래프

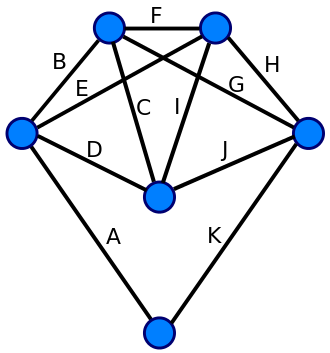
어느 한 정점에서 출발하고, 모든 변을 지나, 원래의 정점으로 돌아올 수 있는 경로가 존재하는 그래프를 "오일러 그래프"라고 부른다.

증명이 다소 복잡하지만, 연결된 무향 그래프가 오일러 그래프라면 해당 그래프는 "각 정점에 연결된 변의 수가 짝수이다." 라는 특징이 존재한다.

  • 트리 구조

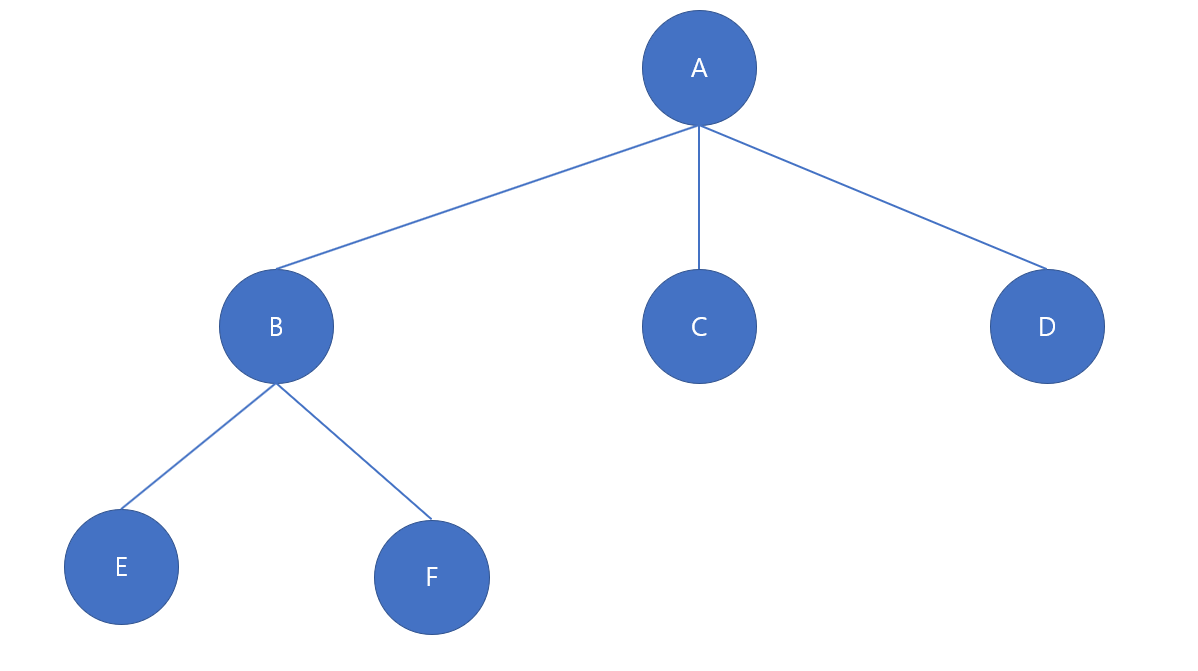
연결된 무향 그래프 중 같은 정점을 두 번 지나지 않고 원래 정점으로 돌아가는 경로가 없는 그래프를 트리라고 부른다.

트리 구조의 특징으로는 변의 수가 정점의 수 보다 1개만큼 적다. 또한 사이클이 없는 그래프다.(어떤 노드도 자기 자신으로 돌아오는 경로가 없다.)

  • 그 외 그래프

    • 완전 그래프 Complete Graph
      무향 그래프 중에서 모든 정점 사이에 변이 하나씩 있는 그래프다.
    • 정규 그래프 Regular Graph
      무향 그래프 중에서 모든 정점의 차수가 같은 그래프
    • 완전 이분 그래프 Complete Bipartite Graph
      이분 그래프 중에서 다른 색으로 칠할 수 있는 모든 정점 사이에 뱐이 1개씩 존재하는 그래프
    • 유향 비순환 그래프 Directed Acyclic Graph, DAG
      유향 그래프 중에서 같은 정점을 구번 지나지 않고 원래 정점으로 돌아올 수 있는 경로가 없는 그래프

그래프 구현

그래프를 구현하는 방법으로 특정한 노드와 인접한 노드를 리스트로 정리하는 '인접 리스트'로 표현하는 방버이 있다.

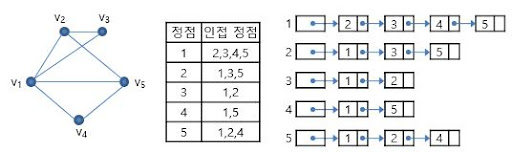
인접 리스트 표현은 (정점의 수) + (변의 수)와 비례하는 만큼의 메모리 용량만 사용한다. 따라서 변의 수가 수백만 개라고 해도, 소비하는 메모리는 100MB100MB 정도가 된다.

class Code_4_05_1 {
	public static void main(String[] args) {
		// 입력
		Scanner sc = new Scanner(System.in);
		int N = sc.nextInt();
		int M = sc.nextInt();
		int[] A = new int[M + 1];
		int[] B = new int[M + 1];
		for (int i = 1; i <= M; i++) {
			A[i] = sc.nextInt();
			B[i] = sc.nextInt();
		}
		
		// 인접리스트 작성
		ArrayList<Integer>[] G = new ArrayList[N + 1];
		for (int i = 1; i <= N; i++) {
			G[i] = new ArrayList<Integer>(); // G[i]는 정점i와 인접한 정점 리스트
		}
		for (int i = 1; i <= M; i++) {
			G[A[i]].add(B[i]); // 정점 A[i]와 인접한 정점으로 B[i]를 추가
			G[B[i]].add(A[i]); // 정점 B[i]와 인접한 정점으로 A[i]를 추가
		}
		
		// 출력(G[i].size()는 정점 i에 인접한 정점 리스트의 크기이므로 "차수"입니다).
		for (int i = 1; i <= N; i++) {
			System.out.format("%d: {", i);
			for (int j = 0; j < G[i].size(); j++) {
				if (j >= 1) {
					System.out.print(",");
				}
				System.out.print(G[i].get(j)); // G[i].get(j)는 정점i와 인접한 정점 중에서 j번째 정점
			}
			System.out.println("}");
		}
	}
}

깊이 우선 탐색 DFS

이동할 수 있는 만큼 이동한 후, 더 이상 이동할 수 없는 정점에 도달했을 때 이전 정점으로 돌아와서 다른 길로 다시 이동하는 알고리즘

동작 과정

  • 모든 정점을 흰색으로 표시
  • 특정 정점으로 이동하고 해당 정점을 회색으로 표시
  • 아래의 두가지 동작을 반복을 한다. 만약 첫 정점으로 돌아올 경우 종료
    • 인접한 정점이 모두 회색일 경우, 이전 정점으로 돌아간다.
    • 그렇지 않은 경우, 현재 정점을 회색으로 표시한 뒤, 인접한 흰색으로 칠해진 정점 중에서 번호가 가장 작은 정점으로 이도
  • 최종적으로 모든 정점이 회색일 경우 그래프가 연결된 것이다.

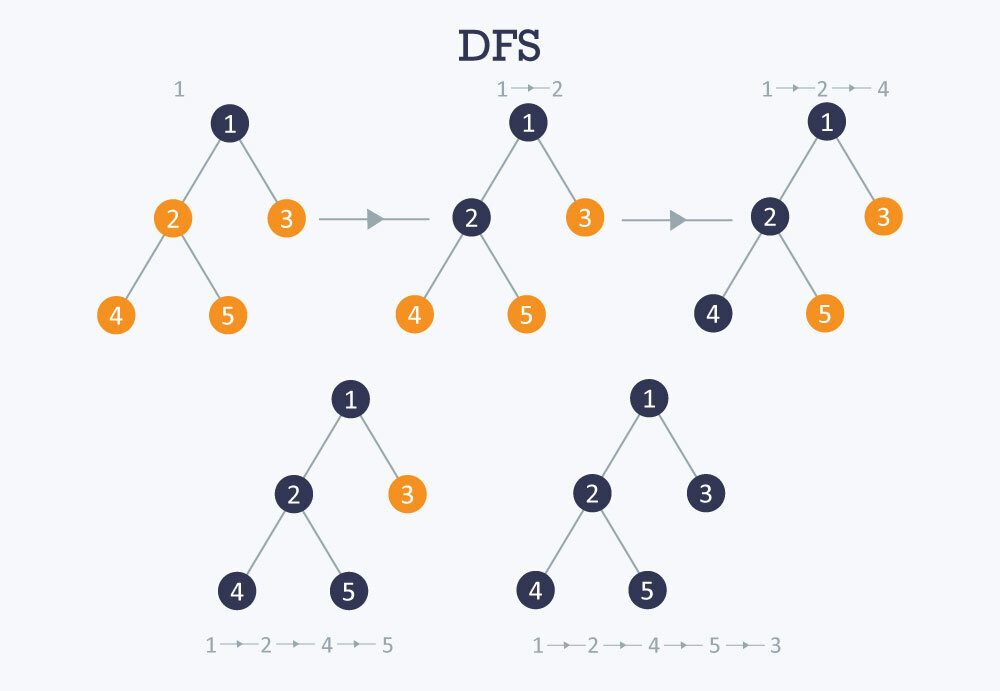
깊이 우선 탐색을 구현하는 대표적인 방법으로는 배열 또는스택을 사용하는 방법과 다음으로는 재귀 함수를 이용하여 구현하는 방법이 있다.

아래는 재귀 함수를 이용한 코드이다.

class 구현1 {
	public static void main(String[] args) throws IOException {
		// 입력(빠른 입출력을 위해서, Scanner 대신에 BufferedReader를 사용했습니다)
		BufferedReader buff = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		st = new StringTokenizer(buff.readLine());
		int N = Integer.parseInt(st.nextToken());
		int M = Integer.parseInt(st.nextToken());
		int[] A = new int[M + 1];
		int[] B = new int[M + 1];
		for (int i = 1; i <= M; i++) {
			st = new StringTokenizer(buff.readLine());
			A[i] = Integer.parseInt(st.nextToken());
			B[i] = Integer.parseInt(st.nextToken());
		}
		
		// 인접리스트 작성
		G = new ArrayList[N + 1];
		for (int i = 1; i <= N; i++) {
			G[i] = new ArrayList<Integer>();
		}
		for (int i = 1; i <= M; i++) {
			G[A[i]].add(B[i]);
			G[B[i]].add(A[i]);
		}
		
		// 깊이 우선 탐색
		visited = new boolean[N + 1];
		for (int i = 1; i <= N; i++) {
			visited[i] = false;
		}
		dfs(1);

		// 연결 판정(answer = true일 때 연결)
		boolean answer = true;
		for (int i = 1; i <= N; i++) {
			if (visited[i] == false) {
				answer = false;
			}
		}
		if (answer == true) {
			System.out.println("The graph is connected.");
		}
		else {
			System.out.println("The graph is not connected.");
		}
	}
	
	static boolean[] visited;
	static ArrayList<Integer>[] G;
	static void dfs(int pos) {
		visited[pos] = true;
		for (int i : G[pos]) {
			if (visited[i] == false) {
				dfs(i);
			}
		}
	}
}

다음으로 스택을 이용하여 구현한 코드이다.

class 구현2 {
	public static void main(String[] args) throws IOException {
		// 입력(빠른 입출력을 위해서, Scanner 대신에 BufferedReader를 사용했습니다)
		BufferedReader buff = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		st = new StringTokenizer(buff.readLine());
		int N = Integer.parseInt(st.nextToken());
		int M = Integer.parseInt(st.nextToken());
		int[] A = new int[M + 1];
		int[] B = new int[M + 1];
		for (int i = 1; i <= M; i++) {
			st = new StringTokenizer(buff.readLine());
			A[i] = Integer.parseInt(st.nextToken());
			B[i] = Integer.parseInt(st.nextToken());
		}
		
		// 인접리스트 작성
		ArrayList<Integer>[] G = new ArrayList[N + 1];
		for (int i = 1; i <= N; i++) {
			G[i] = new ArrayList<Integer>();
		}
		for (int i = 1; i <= M; i++) {
			G[A[i]].add(B[i]);
			G[B[i]].add(A[i]);
		}
		
		// 깊이 우선 탐색 초기화
		boolean[] visited = new boolean[N + 1];
		for (int i = 1; i <= N; i++) {
			visited[i] = false;
		}
		Stack<Integer> S = new Stack<>(); // 스택 S 정의
		visited[1] = true;
		S.push(1); // S에 1을 추가

		// 깊이 우선 탐색
		while (S.size() >= 1) {
			int pos = S.pop(); // S의 앞부분을 확인하고 꺼냄
			for (int nex : G[pos]) {
				if (visited[nex] == false) {
					visited[nex] = true;
					S.push(nex); // S에 nex를 추가
				}
			}
		}
		
		// 연결 판정(answer = true일 때 연결)
		boolean answer = true;
		for (int i = 1; i <= N; i++) {
			if (visited[i] == false) {
				answer = false;
			}
		}
		if (answer == true) {
			System.out.println("The graph is connected.");
		}
		else {
			System.out.println("The graph is not connected.");
		}
	}
}

너비 우선 탐색 BFS

출발 지점과 가까운 정점부터 차례대로 확인한다.

너비 우선 탐색은 큐라는 자료 구조를 구현하는 경우가 많다.

Queue


큐는 이미지와 같이 3가지 동작을 하는 자료 구조이다.

  • 큐의 가장 뒤에 요소를 추가를 한다.
  • 큐의 가장 앞 요소를 확인한다.
  • 큐의 가장 앞 요소를 제거한다.

이러한 Queue의 동작을 이용하여 너비 우선 탐색을 해결할 수 있다.

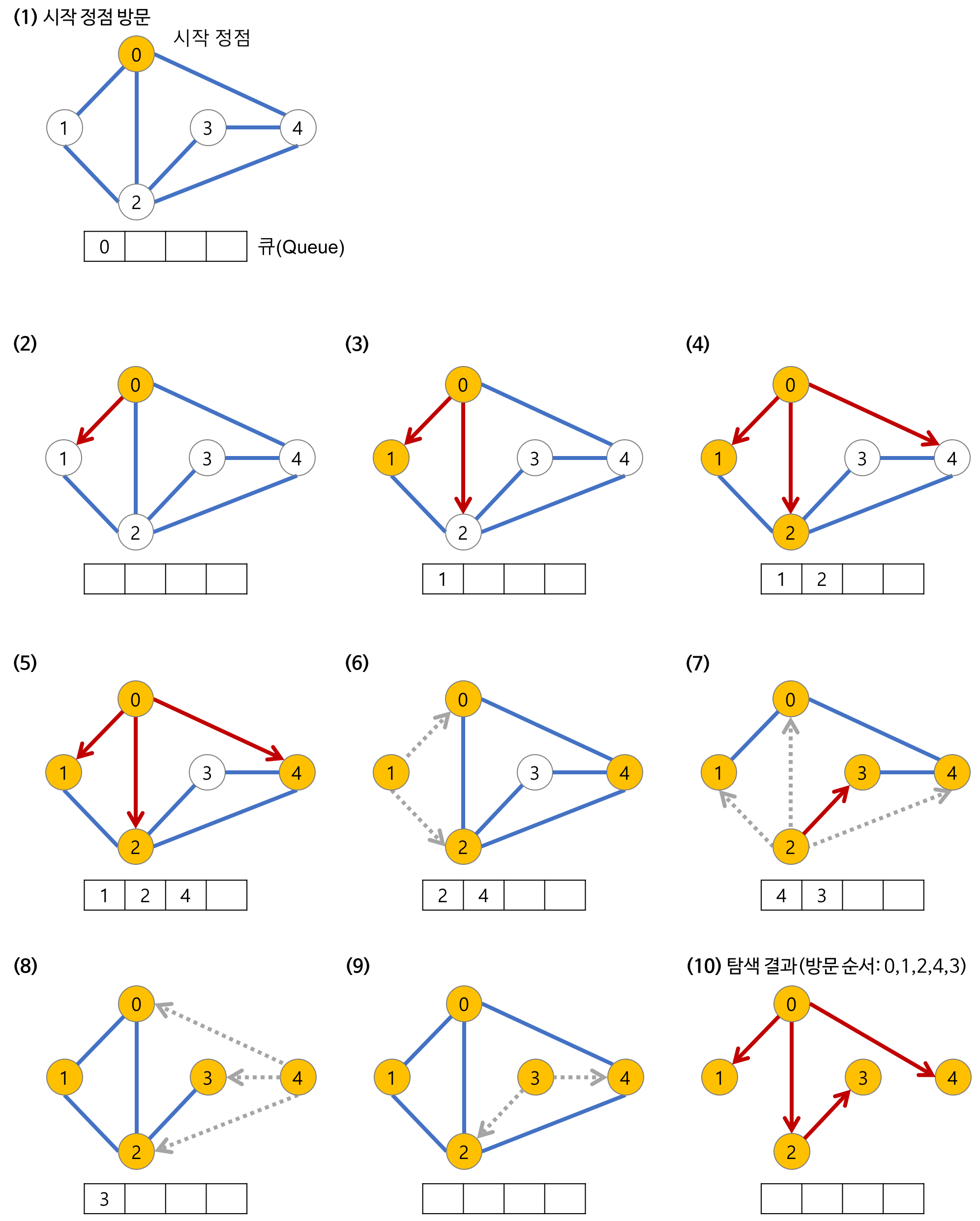
동작 과정

  • 모든 정점을 흰색으로 표시
  • 큐에 정점을 추가하고, 해당 정점을 회색으로 표시
  • 큐가 완전히 빌 때까지 아래의 동작을 반복
    • 큐의 가장 앞 요소를 확인
    • 확인한 요소를 제거
    • 해당 정점과 인접한 흰색 정점으로 이동 후, 해당 정점을 큐 뒤에 추가 및 회색으로 표시

BFS 구현에 있어서 노드를 흰색이나 회색으로 표기가 불가능 하기 때문에 ``

class 구현3 {
	public static void main(String[] args) throws IOException {
		// 입력(빠른 입출력을 위해서, Scanner 대신에 BufferedReader를 사용했습니다)
		BufferedReader buff = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		st = new StringTokenizer(buff.readLine());
		int N = Integer.parseInt(st.nextToken());
		int M = Integer.parseInt(st.nextToken());
		int[] A = new int[M + 1];
		int[] B = new int[M + 1];
		for (int i = 1; i <= M; i++) {
			st = new StringTokenizer(buff.readLine());
			A[i] = Integer.parseInt(st.nextToken());
			B[i] = Integer.parseInt(st.nextToken());
		}
		
		// 인접리스트 작성
		ArrayList<Integer>[] G = new ArrayList[N + 1];
		for (int i = 1; i <= N; i++) {
			G[i] = new ArrayList<Integer>();
		}
		for (int i = 1; i <= M; i++) {
			G[A[i]].add(B[i]);
			G[B[i]].add(A[i]);
		}
		
		// 너비 우선 탐색 초기화(dist[i] = -1일 때 아직 도달하지 않은 흰색 정점으로 취급)
		int[] dist = new int[N + 1];
		for (int i = 1; i <= N; i++) {
			dist[i] = -1;
		}
		Queue<Integer> Q = new LinkedList<>(); // 큐 Q 정의
		dist[1] = 0;
		Q.add(1); // Q에 1을 추가(조작1)

		// 너비 우선 탐색
		while (Q.size() >= 1) {
			int pos = Q.remove(); // Q의 앞을 확인하고, 이를 꺼냄(조작2, 3)
			for (int i = 0; i < G[pos].size(); i++) {
				int nex = G[pos].get(i);
				if (dist[nex] == -1) {
					dist[nex] = dist[pos] + 1;
					Q.add(nex); // Q에 nex를 추가(조작1)
				}
			}
		}
		
		// 정점1에서 각 정점까지의 최단 거리를 출력
		for (int i = 1; i <= N; i++) {
			System.out.println(dist[i]);
		}
	}
}

그 외 알고리즘

  • 단일 시작점 최단거리 문제

    어떠한 시작점에서 각 정점까지의 최단 거리 길이를 구현하는 문제가 된다.
    가중치 없는 그래프의 경우 너비 우선 탐색으로 시간복잡도O(N+M)O(N+M) 시단 내에 해결이 가능하다. 추가적으로 가중치 있는 그래프일 경우, 데이크스트라 알고리즘으로 O(N2)O(N^2) 시간에 해결이 가능하다. 여기서 우선순위 큐라는 자료 구조를 사용하면 O(MlogN)O(M logN)으로 해결이 된다.

  • 모든 정점까지의 최단 경로 문제

    모든 두 정점 조합 사이 최단 경로를 구하는 문제이다. 플로이드-워셜(Warshall-Floyd) 알고리즘을 사용하면 O(N3)O(N^3) 시간에 해결할 수 있다. 큐 등의 자료 구조들을 사용하지 않아도, 단순한 삼중 반복문으로도 구현이 가능한 특징이 있다.

문제 해결을 위한 알고리즘 with 수학 서적의 내용을 참조하여 작성했다.

profile
buckshot
let's go insane
이전 포스트

[알고리즘] - 해시 (Hash)

다음 포스트

[알고리즘] - 경우의 수

0개의 댓글