
정렬
정렬이란 여러 데이터를 특정 순서로 나열하는 조작
예를 들어 아래와 같은 조작이다.
- 오름차순 : [31, 41, 55, 22] -> [22, 31, 41, 55]
- 내림차순 : [5, 2, 3, 2, 3, 8] -> [8, 5, 3, 3, 2, 2]
- 사전 순 : ["algo", "mast", "er"] -> ["algo", "er", "masr"]
선택 정렬
선택 정렬은 아직 정렬되지 않은 대상들 중에서 가장 작은 수를 찾는 조작을 반복하며, 배열을 정렬하는 방법이다.
- 기본적인 흐름
1. 정렬되지 않은 부분(A부터 Z까지)에서 가장 작은 요소를 찾는다.
2. 가장 작은 요소를 A요소와 바꾼다.
3. 다음으로 작은 요소를 찾는다.
이 작업을 반복해서 오름 차순으로 정렬
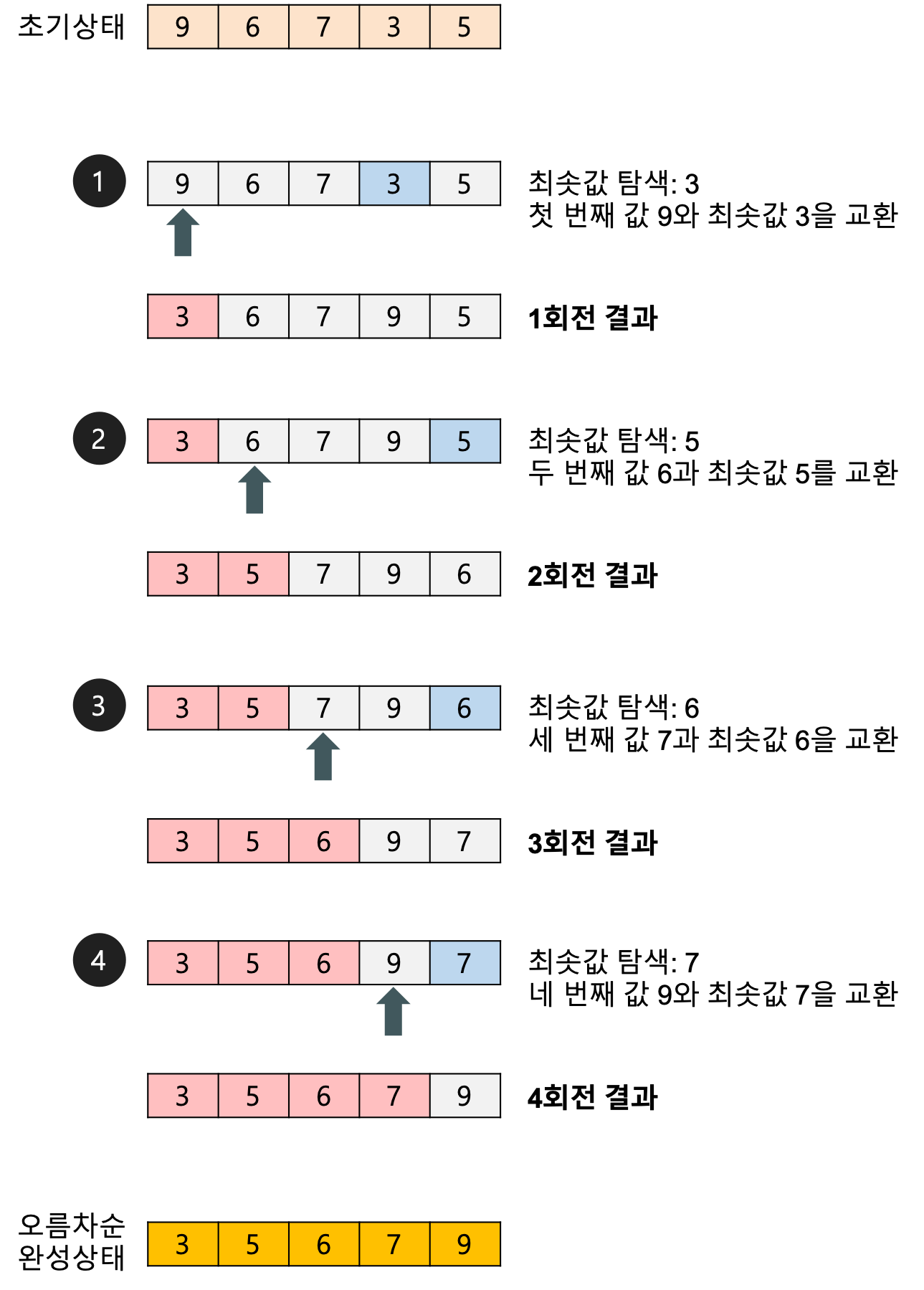
N개의 수 중에서 최솟값을 찾으려면, N-1회 비교를 해야 할 것이다.
그리고 전체적인 정렬을 완성하기 위해서는 각 각의 비교를 N-1회, N-2회, N-3회, ..., 2회, 1회 전체적으로 N(N+1)/2회 비교를 한다.
그런데 N의 수가 커지면 커지는 만큼 작업에 소요되는 시간이 많이 소모가 된다.
N의 값이 증가되면서 길어지는 작업 속도를 개선하기 위해서 '재귀'라는 방법으로 개선이 가능하다.
재귀
자기자신을 인용하는 형태로 정의하는 것을 재귀적 정의라고 하고,
이와 관련하여 자기자신을 호출하는 함수를 재귀함수라고 한다.
재귀적 정의를 사용하면, 알고리즘의 흐름을 보다 간결하게 작성이 가능하며, 프로그램 구현에 있어 편리하게 구현이 가능하게 할 수 있다.
재귀 함수 예제
재귀 함수에서 베이스 케이스가 없을 경우 프로그램이 종료되지 않고 계속 실행이 된다. 이 부분을 주의 해야한다.
- N!(팩토리얼) 계산
static int func(int N) {
if (N == 1) {
return 1; // 베이스 케이스
}
return func(N - 1) * N;
}위 처럼 함수의 동작 순서

- 유클리드 호제법
whlie문을 이용하여 구현 할 수 있지만, 재귀 함수를 사용했을 때 유클리드 호제법의 구현이 간략해진다.
static long GCD(long A, long B) {
if (B == 0) {
return A; // 베이스 케이스
}
return GCD(B, A % B);
}참고로 A가 반드시 B보다 커야 한다.
위 코드 또한 1번 예제와 비슷하게 동작을 한다.
-
분할 정복법으로 합계 계산
1번과 2번 예제레서는 재귀 함수를 내부에 1번 호출을 했지만, 이번에는 자신을 두번 호출을 한다.예를 들어 N개의 정수 A1, A2, ..., A8의 합계를 구하는 문제가 있을 때, 물론 반복문을 사용하여 계산이 가능하다. 하지만 재귀 함수로도 구현이 가능하다.
static int[] A
public static void main(String[] args) {
A = {3, 1, 4, 1}
int answer = solve(1, A.length+1); // result = 9
// 3 + 1 + 4 + 1 = 9
}
static int solve(int l, int r) {
if (r - l == 1) {
return A[l];
}
int m = (l + r) / 2; // 구간 [l, r)의 중앙을 기준으로 분할 정복
int s1 = solve(l, m); // s1는 A[l] + ... + A[m-1]의 합계를 계산
int s2 = solve(m, r); // s2는 A[m] + ... + A[r-1]는 합계를 계산
return s1 + s2;
}병합 정렬
병합 정렬은 N개의 수를 오름 차순으로 정렬하는 알고리즘이다.
병합 정렬은 2개의 정렬된 배열을 결합하는 Merge 조작을 기반으로 한다.
예를 들어 [37, 45, 57, 25]의 값을 갖는 배열을 병합 정렬을 적용을 적용 시켜보겠다.
- 주어진 배열을 두개의 배열로 나눈다.
[37, 45] , [57, 25] - 두개로 나눈 배열을 병합 정렬을 한다.
[37, 45] , [25, 57] - 병합 정렬이 된 두 배열 대상으로 Merge 조작을 한다.
동작 방법
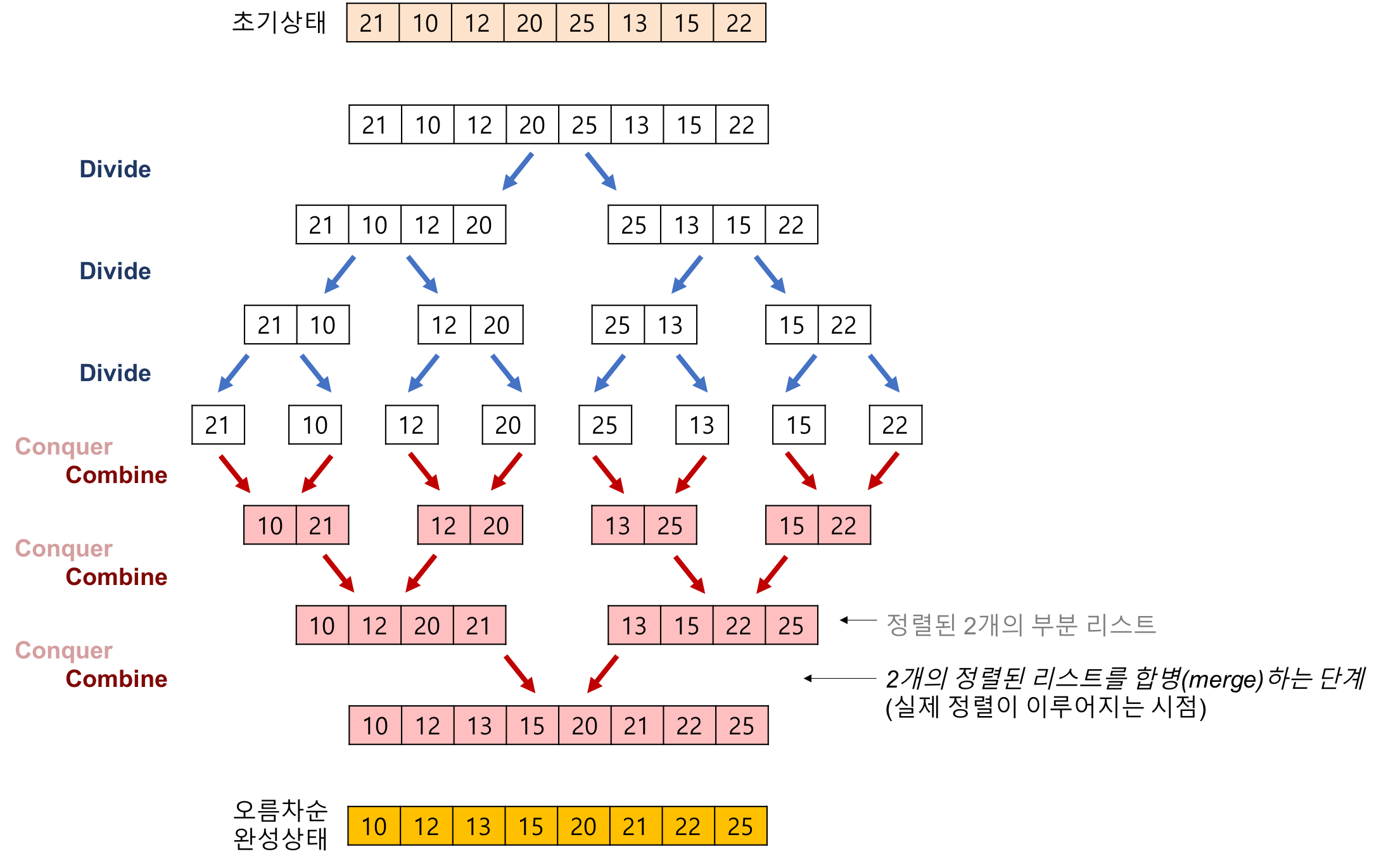
- 병합 정렬의 복잡도
예를 들어 N = 8 이라면- 1번째, 길이가 1인 배열 2개의 Merge(최대 비교 횟수 1회)를 4회
- 2번째, 길이가 2인 배열 2개의 Merge(최대 비교 횟수 3회)를 2회
- 3번째, 길이가 4인 배열 2개의 Merge(최대 비교 횟수 7회)를 1회
- total 비교 횟수 (14)+(32)+(7*1) = 17
앞에서 이야기 했던 선택정렬은 28회(N * (N-1) / 2 = 28) 비교를 한다. 병합 정렬은 약 1.6배의 차이가 난다.
만약, N의 값이 증가를 할 수록 성능 차이는 점 점 더 커진다.
그 외 정렬 알고리즘
-
삽입 정렬
차례대로 앞에서 부터 정렬이 완료된 부분에 요소를 적절하게 삽입하는 작업을 반복하는 알고리즘 -
퀵 정렬
실용적으로 사용이 가능한 알고리즘 중 빠르게 동작을 한다고 알려진 정렬 알고리즘 중 하나다.병합 정렬과 마찬가지로 분할 정복 아이디어를 사용한다.
-
계수 정렬
N개의 숫자에서 최댓값을 B라고 할 때 1의 개수, 2의 개수 .., V의 개수를 세어 배열을 정렬하는 알고리즘이다.
위 나머지 정렬 알고리즘은 나중에 추가적으로 학습하여 정리 하겠다.

