210310_TIL
요즘 잠을 자도 잔 것 같지 않은 날이 부쩍 많아졌다. 침대에 누워 뒤척이다가 새벽에 잠들곤 하는데 컨디션이 정말 좋지 않다. 잠을 제대로 못 자니 눈도 아파오고 잇몸도 아프고 편두통도 생긴 것 같다. 온 몸이 아프니 공부도 제대로 되지 않고 그래서 오늘은 일찍자야지 생각하다가도 또 어려운 문제에 막혀서 생각하다 보면 금방 12시가 지나 있다. 공부를 열심히 하는 것도 좋지만 효율이 너무 안 나오는 것 같다. 아무리 시간을 투자해도 막막하니 조급해지고 자신감도 계속 떨어진다. 그러면 '아직 개발 공부를 시작한지 세 달도 안되었는데 모르는게 당연하지 않아?'라는 자기 위로를 하게 된다. 그러면 또 '아 나 지금 합리화 하는건가?'라는 생각이 들고 결국 무한 루프에 빠지고 만다.
이렇게 자기 관리를 하지 못하면 공부가 어려워 스트레스 받으니 생활리듬이 깨지고 생활리듬이 깨지니 공부가 안되고 공부가 안되니 더 어려워지는 악순환에 빠지고 만다. 이러한 악순환에서 빠져 나오는 가장 좋은 방법은 지금 당장 모르는 문제가 있더라도 여유를 가지고 건강을 챙기면서 공부하는 것이다. 그래도 나름 건강을 위해 하루 세 끼 거르지 않고 이틀에 30분정도 꾸준히 운동을 하고 있다. 가끔 외출을 하고 들어 올 때 계단을 이용해볼까 생각도 하지만 아직 생각만하고 있다.😅
컨디션이 좋지 않아 몸도 마음도 안 따라주지만 업비트에 빨간불만 보면 피곤이 싹 사라지긴한다.😋
Graph
흔히 ppt에서 볼 수 있는 막대 그래프가 아닌
네트워크 망처럼 생겼다.
특징
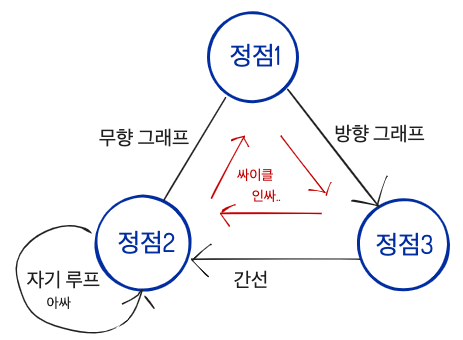
정점(vertex)과 간선(edge)를 가지고 있다.
무향그래프(undirected graph): 정점1에서 정점2로 갈 수 있으면 정점2에서 정점1로 갈 수 있다.
진입차수(in-degree): 한 정점에 들어오는 간선의 수
진출차수(out-degree): 한 정점에서 나가는 간선의 수
어디에 써?
네비, SNS, 검색
내부로직 구현
class Graph() {
constructor() {
this.matrix = []
}
addVertex() { // 정점 추가
const currentLen = this.matrix.length; // 처음 matrix의 길이는 0일테니
for(let src = 0; src < currentLen; src++) { // 반복문이 돌지 않고
this.matrix[src].push(0)
}
this.matrix.push(new Array(currentLen + 1).fill(0) // matrix = [[0]]
}
contains(vertex) { // 정점 있는지 확인
return !!this.matrix[vertex]
// 메트릭스에 정점이 있으면 배열이 반환 => 의 반대 => false => 의 반대 => true
// 메트릭스에 정점이 없으면 undefined => 의 반대 => true => 의 반대 => false
}
addEdege(src, det) { // 간선 추가
const currentLen = this.matrix.length;
if (src === undefined || det === undefined) { // 출발지든 목적지든 하나라도 없으면 간선 추가 못해~
return;
}
if(src + 1 > currentLen || det + 1 > currentLen || src < 0 || det < 0) {
// 출발지나 목적지의 범위가 벗어나버리면 추가 못해~
return;
}
// 예외적인 상황이 아니면 간선 추가
this.matrix[src][det] = 1
}
hasEdge(src, det) { // 간선 있는지 확인
return !!this.matrix[src][det]
}
removeEdge(src, det) {
const currentLen = this.matrix.length;
if (src === undefined || det === undefined) { // 출발지든 목적지든 하나라도 없으면 간선 제거 못해~
return;
}
if(src + 1 > currentLen || det + 1 > currentLen || src < 0 || det < 0) {
// 출발지나 목적지의 범위가 벗어나버리면 제거 못해~
return;
}
// 예외적인 상황이 아니면 간선 제거
this.matrix[src][det] = 0
}
}인접행렬
정점끼리 관계를 나타낸 행렬
모든 간선의 정보를 담고있다.
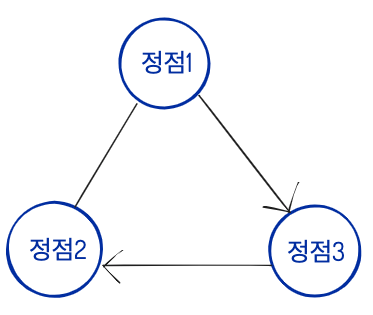
인접행렬
정점1 정점2 정점3
정점1 0 1 1
정점2 1 0 0
정점3 0 1 0이렇게 정점과 정점간의 모든 관계를 써줘야하기 때문에
정점간의 관계를 파악하고
가장 빠른 경로를 찾기 쉽다.
하지만 정점을 추가하고 제거하려면 정점간의 관계를 전부 다시 적어줘야하기 때문에 어려움이 존재한다.
인접리스트
정점을 이어주는 간선의 정보만 나타낸 리스트
정점의 연결관계를 어떤식으로 저장해 두는 지가 핵심

header vertex vertex
정점1 --> 정점2 --> 정점3 --> null
정점2 --> 정점1 --> null
정점3 --> 정점2 --> null정점끼리 연관된 관계만 써주면 되기 때문에
메모리를 차지하는 비율이 적고
직관적으로 어떤 정점이 어떤 정점에 인접한지 알기 쉽다.
정점1은 정점2랑 정점3이랑 인접하네 진출차수 2개, vertex를 보면 정점1이 하나네? 진입차수 1개
정점2는 정점1이랑 인접하네 진출차수 1개
또, 메모리를 차지하는 비율이 적기 때문에
정점의 개수가 간선의 개수보다 월등히 많을 때 사용하기 좋다.
FaceBook의 이용자의 수가 정점이라고 생각해보자
수억? 수십억? 개가 있을 것이다.
그럼 FaceBookdml 이용자간의 관계를 인접행렬로 나타내면
수십억 x 수십억
계산해야 할 데이터가 너무 많다.
하지만 인접리스트로 나타내면
서로 친구 추가되어 있는 사용자간의 관계만 나타내면 되기 때문에
비교적 계산해야할 데이터가 적어진다.
