[GCN 수식 정리] Graph Laplacian and Graph Fourier Transform

GCN 관련 논문을 읽는데 계속해서 Graph Laplacian과 Fourier Transform이라는 용어가 나왔다. 그래서 이 둘이 무엇을 의미하고 어떤 식으로 GCN에서 활용되는지 찾아 보았다.
내용은 다음 블로그를 참고하였다: https://ahjeong.tistory.com/14

---

1. Graph Laplacian

우선, Graph Laplacian은 다음과 같은 이유로 GCN에서 필요한 기술이다.

• 그래프에서 변수(노드) 간의 관계를 나타내기 위해서 필요하다. 즉, 공간 정보를 표현하기 위해 필요하다.
• 구체적으로 하나의 노드에 대해서 주변 노드들과의 difference 값을 환산하여 이를 기준으로 주변 노드와의 유사성을 판단할 수 있다.

그렇다면 Graph Laplacian은 어떻게 구할 수 있을까?

Grpah Laplacian을 구하는 수식은 다음과 같다.

• $D$: Degree Matrix(차수 행렬)
• $A$: Adjacency Matrix(인접 행렬)
• $L$: Laplacian Matrix(라플라시안 행렬)

따라서, $L$을 보고 각 노드의 차수(연결된 edge의 개수)와 연결된 노드 정보를 알 수 있다.

---

예시와 함께 살펴보자.

    (1)───(2)
     |   /
     |  /
    (3)

이 그래프의 정보:

• 노드 집합: $V = \{1, 2, 3\}$
• 간선 집합: $E = \{(1,2), (1,3), (2,3)\}$

여기서, 인접 행렬 $A$는 노드 간 연결 관계를 나타낸다.

• $A_{ij} = 1$이면 노드 $i$와 $j$가 연결됨.
• $A_{ij} = 0$이면 연결되지 않음.

그리고 차수 행렬 $D$는 다음과 같다.
(각 노드의 차수를 대각 행렬로 표현한다.)

• 노드 1: 연결된 간선 2개 → $D_{11} = 2$
• 노드 2: 연결된 간선 2개 → $D_{22} = 2$
• 노드 3: 연결된 간선 2개 → $D_{33} = 2$

라플라시안 행렬 $L$ 계산 과정은 다음과 같다.

$L_{i, i}$ (대각 성분) : 노드의 차수 (연결된 edge의 수)
$L_{i, j}, i \neq j$ (비대각 성분) : i노드와 j노드의 연결 여부 (연결: -1, 비연결: 0)

---

이제 Grpah Laplacian이 무엇인지 알았다 ( $D - A =L$ ).
이를 GCN에 적용하기 위해 좀더 구체화해보자.

다음 수식을 보자.

• $h$ : Difference Operator
• $L$ : Laplacian Matrix
• $f$ : Graph Signal (Feature Matrix)
• $h_{i}$ : $i$번 노드의 difference operator
• $L_{i}$ : $i$번 노드의 Laplacian 행렬
• $D_{i}$ : 차수 행렬 $D$의 $i$번째 행
• $D_{i, i}$ : 차수 행렬 $D$의 $(i, i)$ 요소
• $A_{i}$: 인접 행렬 $A$의 $i$번째 행
• $f_{i}$: $i$번 노드의 feature 행렬

처음 수식을 보고 이해가 잘 되지 않았다. 그래서 의미를 하나씩 찾아 보면서 이해해 갔다.

• 먼저, 라플라시안 행렬 $L$에 graph signal(feature) $f$를 곱해준다. 그리고 이 값을 $h$(difference operator)라고 한다. 수식은 (1)과 같다.
• 그리고 $i$번 노드에 대해서 이를 적용하면 수식 (2)와 같다. 여기서 약간 이해하기 어려웠던 게
  $(D_{i} - A_{i})f = D_{i}f_{i} - A_{i}f = D_{i,i}f_{i} - A_{i}f$ 에서 갑자기 $f$가 $f_{i}$로 변한 부분이다. 그래서 의미적으로 해석을 해봤다.
  • 대각 행렬 $D_{i}$는 $i$번째 행만 고려하며, $A_{i}$도 $i$번째 행만 고려한다.
  • 즉, 대각 행렬과 인접 행렬 모두 $i$번 노드에 대해서만 고려한다.
  • 그리고 대각 행렬의 경우 $i$번 노드만 고려하면 되기에 $f_{i}$만 적용하면 된다.
  • 하지만 인접 행렬의 경우, $i$번 노드뿐만 아니라 이에 인접한 다른 노드 $j$번 노드도 고려해야하기 때문에 여러 개의 $f_{j}$를 적용해야 한다.
  • 그래서 수식이 $D$에 대해서는 $f_{i}$만, $A$에 대해서는 $f$(인접 노드들의 피처 집합)로 나오게 된 것이다.
• 결국 수식을 해석해 보면, $i$번 노드의 feature $f_{i}$를 인접 노드인 $j$번 노드의 feature $f_{j}$들을 뺀 값을 의미하게 된다. 이는 difference operator로서 타당한 수식임음 알 수 있다.

하지만 위 $h$ 값을 가지고 그대로 모델에 적용하기가 힘들다. 왜냐하면 위의 경우 부호 개념(+냐 -냐)이 존재하기 때문에, 단순히 값이 작다고 주변 노드들과 유사성이 높은 노드라고 판단하기 힘들다.
(ex. -100 vs. 5) : 5가 더 유사성이 높은 건데, -100이 5보다 더 작음.
따라서 값에 제곱을 해서 부호를 통일해주어야 한다. (해당 블로그에서는 이 과정을 Laplacian Quadratic Form이라고 부른다.)

Laplacian Quadratic Form의 수식은 다음과 같다.

에서 $Lf$를 제곱하기 보다는 feature인 $f$만 제곱을 해준다. 이를 위해 $f^T$를 곱해준다.

• 위 수식 중 $\frac{1}{2}\sum_{i, j}{A(j, i)f_{i}(f_{i}-f_{j})}$에서 $A(j, i)$가 되는 이유는 인접 행렬 $A$는 대칭 행렬이므로 순서를 바꿔도 동일하기 때문이다. $A(j, i) = A(i, j)$
• 그리고 $\frac{1}{2}\sum_{i, j}{A(j, i)f_{i}(f_{i}-f_{j})}$를 $- \frac{1}{2}\sum_{i, j}{A(i, j)f_{j}(f_{i}-f_{j})}$로 변환하기 위해, $i$와 $j$를 서로 바꿔준다(Transpose).
  • $i(i-j) = i^2 - ij$ >>>(Transpose)>>> $j^2 - ji = j(j - i) = -j(i - j)$
• 따라서 Laplacian Quadratic Form인 최종 수식 $\frac{1}{2}\sum_{i, j}{A(i, j)(f_{i}-f_{j})^2}$을 얻게 된다.

결론적으로, Laplacian Quadratic Form을 보고 해당 노드의 signal(feature)이 주변 노드 signal(feature)와 얼마나 유사한지(smooth 한지, frequent 한지) 판단할 수 있다.

• Laplacian Quadratic Form 값이 크다 = grpah signal 간의 차이가 크다
• Laplacian Quadratic Form 값이 작다 = grpah signal 간의 차이가 작다

---

2. Pourier Transform

그렇다면 이제 주어진 그래프에 대해, 연결된 node끼리 feature를 유사하게 하고 noise를 제거하여 graph node feature를 update하고 싶은 경우(= graph filtering 혹은 smoothing을 원할 경우) Laplacian Quadratic Form의 값을 최소화하는 $f$(feature or signal)를 구하면 되겠다.
(블로그 내용)

그렇다면 어떻게 Laplacian Quadratic Form의 값을 최소화하는 $f$(feature or signal)를 구할 수 있을까?

Laplacian Quadratic Form을 최소화하는 최적의 $f$(feature or signal)는 라플라시안 행렬 $L$에 속하는 eigenspace에 속하는 벡터라고 한다.
즉, $L$의 eigenvector들이 Laplacian Quadratic Form을 최소화하는 최적의 $f$이다.

그리고 라플라시안 행렬 $L$의 eigenvalue와 eigenvector는 다음과 같다.

• $\lambda$: eigenvalue
• $u$: eigenvector

그리고 우변의 $u$를 좌변으로 넘겨서 수식을 정리하면 다음과 같아진다.

아까 Laplacian Quadratic Form과 동일한 형태를 띠고 있는 것을 확인할 수 있다.
Laplacian Quadratic Form : $f^TLf$

• 따라서 $u_i^TLu_i$은 Laplacian Quadratic Form을 의미하게 되고, 이를 통해 graph signal의 smoothness 값을 구할 수가 있다.
• 즉, 라플라시안 행렬 $L$을 decomposition하면, $N$개의 eigenvector들과 eigenvalue들을 얻을 수가 있다. 그리고 이때 각각의 eigenvalue들은 각 eigenvector u의 smoothness 정도를 나타낸다.

---

그렇다면 이제 Laplacian Quadratic Form을 푸리에 변환에 적용해보자.

결론부터 말하면, 위 그림과 같이 graph fourier transform은 라플라시안 행렬 $L$을 eigen decomposition하여 eigenvector들의 합으로 signal $f$를 표현하는 것이다.
따라서, graph signal을 기존의 spatial 공간에서 frequency를 나타내는 spectral 공간으로 변환하는 것이다.

즉, 다음과 같이 의미를 해석할 수 있다.

• 작은 eigenvalue를 갖는 eigenvector의 경우 graph를 더욱 smooth하게 나누는 기준이 되며, node간의 유사한 특징 정보를 담고 있다고 볼 수 있다.
• 반대로 큰 eigenvalue를 갖는 eigenvector의 경우 node간 서로 다른 특징의 정보를 많이 담고 있다고 볼 수 있다.

또한, 위 이미지를 보면,
(1) spatial domain --(by Decomposition)--> spectral domain
(2) spectral domain--(by Reconstruction)--> spatial domain
의 과정을 볼 수가 있다. 왜 굳이 이런 방법을 택하는 걸까?

그 이유는 graph signal을 frequency의 조합인 spectral domain에서 표현한 후, 다시 spatial domain으로 복원할 때 사용되는 filter를 학습함으로써 graph signal의 noise를 제거하고 필요한 성분만을 남긴 후 node를 embedding하기 위해서이다.

---

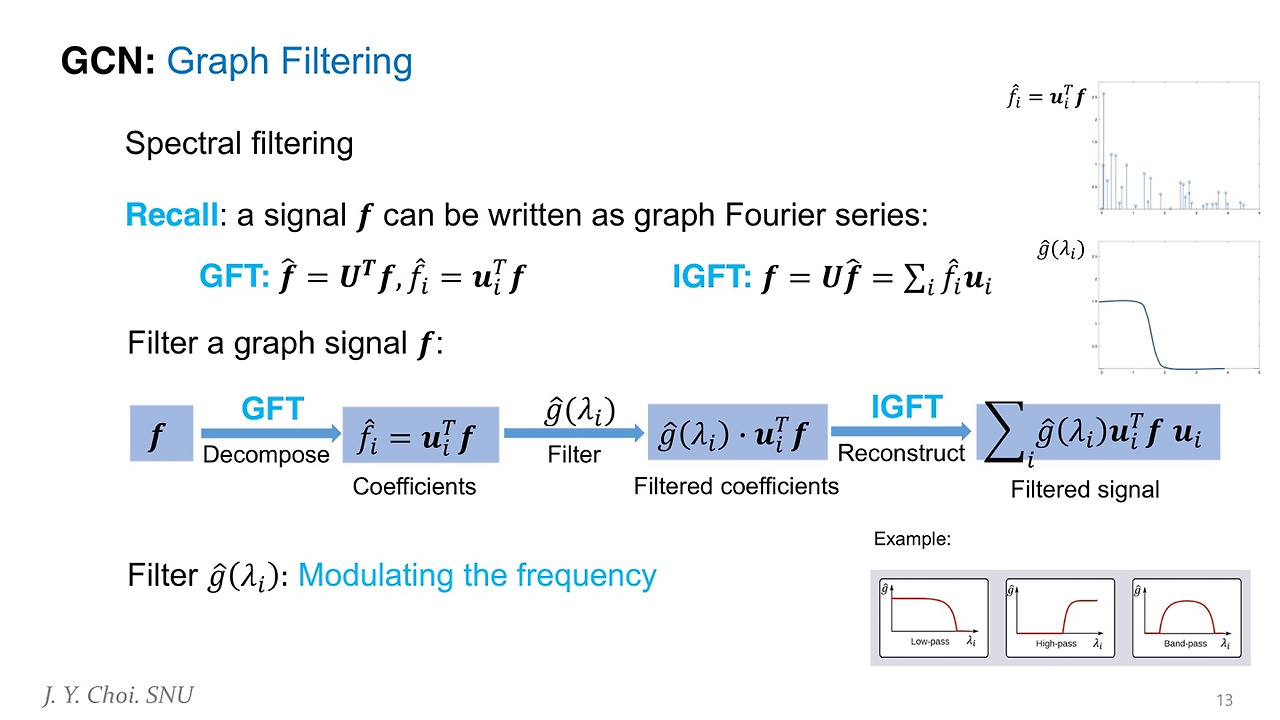
위 이미지는 GCN의 Grpah Filtering 과정을 잘 나타낸다.

1. 먼저 GFT(Graph Fourier Transform)을 통해 signal $f$를 decompose한다.
2. 이후 decompose된 각각의 fourier 계수 $\hat{f_{i}}에$ $\hat{g}(λ_i)$를 곱한다(filter를 적용한다).
3. 그리고 IGFT(Inverse Graph Fourier Transform)을 통해 다시 spatial 공간으로 정보를 보낸다(Reconstruct한다).

이때 $g(.)$가 학습해야 할 filter이다. filter $g(.)$는 여러 개의 frequency signal 중 어떤 걸 사용할지 거르는(필터링) 역할을 한다.

이미지의 오른쪽 위 두 그래프에서, $\hat{f_i}$는 fourier 계수(frequency)를 의미하며, $\hat{g}(λ_i)$은 filter를 의미한다.
위 그래프를 통해, filter를 사용하는 앞쪽의 frequency들만 사용하고 뒤쪽의 frequency는 사용하지 않는다는 것을 확인할 수가 있다.

---

3. 결론

https://ahjeong.tistory.com/14 블로그를 통해 Graph Laplacian과 Graph Pourier Transform을 배울 수 있었다. 라플라시안의 경우 어느 정도 이해가 됐지만, 푸리에 변환의 경우 아직 완전히 이해가 되지 않는다. 따라서 이후 푸리에 변환에 대한 더 구체적인 정보를 찾아 볼 계획이다.